Взаимодействие агентов со средой

Агенты обычно функционируют в некоторой среде, и взаимодействие со средой является важной задачей агента. Роль среды для агентов играет либо активный объект, в который вложены агенты, либо в качестве среды может быть использован другой активный объект. На рис. 15.4 в качестве среды может выступать либо корневой объект Model, либо объект world. Этот ри­сунок повторяет рис. 7.12 главы 7. Среда может быть пассивной либо иметь свое поведение: это тоже активный объект. Динамика среды может задавать­ся уравнениями, стейтчартом, потоковой диаграммой, использованием тай­меров и т. д. Например, у среды может быть тактовый таймер, который циклически запускает вызов функции обращения к агентам для их продви­жения или выполнения ими собственных операций. Функционирование агентов в такой среде можно назвать синхронным в отличие от асинхронно­го их функционирования, когда каждый агент имеет свои собственные сред­ства продвижения времени.

Средства взаимодействия среды с агентом указаны на рис. 15.3. Однако если агентов несколько, то необходимо указать конкретный элемент множества агентов. Например, чтобы вызвать функцию function i-ro агента из объекта Model (рис. 15.4), нужно записать:

agent.item(i).function(...);

Для того чтобы получить доступ из объекта Model ко всем агентам, нужно организовать цикл, например:

for(int i=0; i < agent.size (); i++){

Agent a = agent. item(i),-

// делать что-то с агентом а }

Если необходимо то же сделать из объекта world, нужно сначала в активном объекте world построить указатель на включающий его объект. Пусть этот указатель будет назван owner:

Model owner = (Model)getOwner();

После этого вызов функции у i-ro агента из объекта world можно выпол­нить так:

owner.agent.item(i).function(...);

Конечно, это можно сделать и не вводя указателя явно, но это громоздко:

((Model)getOwner()).agent.item(i);

Точно также организуется доступ к среде из агента. Пусть, например, в ар­хитектуре, изображенной на рис. 15.4, необходимо в переменной х корнево­го объекта Model подсчитывать общее число агентов, находящихся в состоя­нии MiddieAge, т. е. лиц среднего возраста в соответствии со стейтчартом рис. 15.2. Для этого определим указатель на включающий объект:

Model m = (Model(getOwner();

При входе в состояние MiddieAge каждый агент должен выполнить опе­рацию:

т.х++;

а при выходе из этого состояния агент должен выполнить операцию:

Т.х--;

Определив эти действия в стейтчарте класса Agent, который является, фак­тически, шаблоном для построения агентов, мы добьемся желаемого резуль­тата. Такой же подсчет может выполнять и сама среда: при синхронной ор­ганизации функционирования агентов в активном объекте, представляющем среду, можно организовать цикл по всем агентам, проверяя в цикле состоя­ние каждого агента.

15.6. Взаимодействие агентов
с другими агентами

Взаимодействие агентов обычно осуществляется через среду. Чтобы из неко­торого агента получить доступ к другому агенту, сначала нужно определить указатель на этого "другого" агента. Этот указатель может быть введен как переменная типа Agent графически в поле редактора активного объекта Agent или просто описан:

Agent other;

в поле Дополнительный код класса окна Код этого объекта. Далее, как было описано ранее, определяем указатель на объект, включающий вектор аген­тов. Пусть, как на рис. 15.4, этот включающий объект имеет имя Model:

Model m = (Model)getOwner();

Для обращения к конкретному агенту с номером i нужно выполнить вызов именно i-гo элемента вектора agent:

other = m.agent.item(i);

Для выбора случайного другого агента данный агент может выбрать случай­ного агента, но проверить при этом, не совпадает ли выбранный агент с ним самим:

do

other = m.agent.random(); while(other == this);

Теперь, когда мы имеем прямой указатель other на другого агента, к этому агенту уже можно обратиться так:

other.function();

ИЛИ.

other.port. receive (...);

И Т. Д.

Агенты в пространстве

Широко распространенными задачами, связанными с агентами, являются задачи физического перемещения агентов в пространстве. Рассмотрим неко­торые типичные задачи этого класса. Пусть в активном объекте Agent опре­делены вещественные переменные х, у и vx, vy, которые хранят координа­ты агента и его скорости по координатам в двумерном пространстве. Пусть также активный объект, в который будет включено реплицированное мно­жество agent (экземпляров класса Agent), называется Environment. Приве­дем несколько очевидных функций, которые полезны при моделировании движения агента (рис. 15.5).

О Поместить себя в случайную позицию пространства с размерами width и height:

х = uniform(width);

у = uniform(height);

О Переместиться в пространстве за единицу времени при скорости vx, vy:

х += vx;

у += vy;

□ Определить в активном объекте Environment глобальную функцию рас­стояния:

double distance) Agent a, Agent Ь) { double dx = a.x - b.x; double dy = а.у - b.y return sqrt(dx*dx + dy*dy);

^}

- Найти всех агентов в радиусе r:

Environment env = (Environment)getOwner(); for(int i=0; i<env.agent.size(); i++)

if(env.distance(this, env.agent.item(i)) < R)

//сделать что-то с каждым найденным близким агентом...

Рассмотрим теперь вариант двумерного упорядоченного пространства, в ка­ждой клетке которого может находиться произвольное число агентов (рис. 15.6).

Пусть снова включающий агентов активный объект имеет имя Environment. Каждая клетка с точки зрения модели — это контейнер произвольного чис­ла агентов, причем количество агентов в клетке может меняться динамиче­ски, в процессе работы модели. Такой тип данных языка Java нами был рас­смотрен в главе 7, это класс vector.

Класс vector имеет несколько полезных методов. Пусть cell — объект типа

Vector.

□ Получить число элементов вектора:

cell.size();

F

□ Добавить объект agentA в вектор cell:

cell.add(agentA);

□ Выбросить объект agentA из вектора cell:

cell.remove(agentA);

□ Получить i-й элемент вектора:

(Agent)cell.get(i);

Этот последний случай следует прокомментировать. Вектор в языке Java мо­жет содержать объекты любого типа, он рассматривает их все как экземпляры наиболее абстрактного типа object. Поэтому и возвращаемый методом get объект будет иметь тип object. Чтобы его привести к тому типу, с которым мы работаем, т. е. типу Agent, нужна операция кастинга, приведения типов.

Для того чтобы инициализировать массив векторов-клеток с именем cells размером nxm во включающем агентов объекте (каждая клетка — это вектор объектов типа Agent), нужно записать:

cells = new Vector[n][m]; fort int r=0; r<n; r++)

for(int c=0; c<m; C++)

cells[r][c] = new Vector();

Пусть в активном объекте Agent определен указатель на этот массив векто­ров с тем же именем cells:

Vector[][] cells = ((Environment)getOwner()).cells;

Приведем несколько полезных функций, которые могут использоваться при моделировании движения агентов в таком пространстве. Пусть в агенте оп­ределены две целых переменных r, с, которые задают номер клетки, в кото­рой находится этот агент.

□ Найти случайную клетку и поместить в эту клетку себя:

г = uniform_discr(0,п-1); с = uniform_discr(0,m-l); cells[г][с].add(this);

□ Переместиться вправо на 1 клетку, удалив себя из текущей клетки:

cells[г][с++].remove(this); cells[г][с].add(this);

□ Найти количество агентов в клетке снизу:

int N = cells[r+1] [с].size ();

□ Найти случайного агента в данной клетке с индексами r, c:

int k = uniform_discr(0,cells[r][с].size()-1); // случайный номер Agent a = (Agent)cells[r][с].get(к);

Поскольку в этой операции используется метод get класса vector, то здесь также необходима операция кастинга, т. е. приведение возвращенного этим методом объекта типа object к типу Agent, объекты которого запомнены в векторе.

Рассмотрим теперь случай, когда в модели агенты функционируют в среде, которая разбита на несколько локальных районов, в каждом из которых мо­жет находиться некоторое число агентов. При этом в модели неважно физи­ческое расстояние как между районами, так и между агентами, находящи­мися в одном районе (рис. 15.7).

Пусть в редакторе определен реплицированный объект — вектор агентов с именем agent, которые все являются экземплярами класса Agent (рис. 15.7). Пусть также этот вектор вложен в класс (активный объект) Environment, и в этом классе определен вектор с именем locations. Каж­дый элемент этого вектора может хранить любое число экземпляров агентов, т.е. location[i] является i-м "местом", в которое может быть помещено произвольное число агентов. Для того чтобы инициализировать этот массив "мест" в среде, следует в активном объекте Environment сначала создать мас­сив указателей на вектора, например, из 25 штук: Vector [ ] locations = new Vector[25];

а потом создать сами объекты — пустые вектора:

for(int i=0; i<25; i++)

locations[i] = new Vector();

Рассмотрим теперь, что может делать агент, если в классе, в который он бу­дет вложен, определен массив таких "мест". Во-первых, в агенте следует иметь указатель на включающий объект. Назовем его env: Environment env = ((Environment)getOwner());

Теперь из агента доступ к массиву векторов получить просто — это env. locations. Пусть в агенте описана переменная location типа vector (рис. 15.7). Приведем примеры операций, которые можно выпол­нить в агенте.

□ Поместить себя в случайное "место" в среде:

int k = unifrom_discr(0, locations.length-1) location = env.locations[ к ]; location.add(this);

□ Удалить себя из текущего "места":

location.remove(this);

□ Найти количество агентов в том "месте", в которое помещен агент:

int N = location.size();

□ Найти случайного агента в том "месте", в которое помещен агент:

int k = unifrom_discr(0, locationo.length-1) Agent a = (Agent)location.get(к);

Здесь снова используется метод get класса vector, поэтому возвращаемый этим методом объекта типа object приводится к типу Agent.

15.8. Пример агентной модели: Инфицированные муравьи

Инфицированные муравьи (contagious Ants) — это агентная модель искусственной жизни, в которой реализовано простое коллективное поведе­ние активных объектов. В модели агенты-муравьи двигаются в ограничен­ном двумерном пространстве, стараясь избегать столкновений друг с другом и "отражаясь" от стенок. Кроме того, каждый муравей выступает и в другой роли: он может быть инфицирован либо с некоторой вероятностью спон­танно, либо встретив инфицированного муравья. Он может вылечиться либо сам по прошествии некоторого времени, либо встретив на своем пути мура­вья специального типа, которого назовем доктором.

Определив индивидуальное поведение каждого из многих активных объек­тов независимо, мы можем затем наблюдать в агентной модели, как коллек­тивное поведение всей системы порождается из этих индивидуальных пове­дений и как характеристики этого коллективного поведения зависят от индивидуальных параметров членов коллектива. Это именно то, что дает агентное моделирование.

Наблюдение модели

Модель находится в папке Model Examples\Part IV. Откройте и запустите модель. Анимация модели представлена на рис. 15.8.

В окне анимации вы видите поле анимации, на котором хаотично движутся и иногда останавливаются муравьи. Некоторые из них красные — они ин­фицированы. Некоторые — черные, это доктора.

Динамика этой популяции представлена в двух независимых активностях. Первая активность — это движение. При движении муравьи отражаются от стен и стараются не сталкиваться с другими муравьями. Для того чтобы из­бежать столкновения, муравей при встрече с другим муравьем останавлива­ется и ждет некоторое время, причем на время ожидания он сворачивается. Затем он продолжает движение в случайно выбранном направлении. Траек­тория движения некоторых случайно выбранных муравьев отслеживается, эти муравьи отмечены зеленым кружком, траектория их движения рисуется за ними. Вторая активность в популяции — это распространение инфекции. Муравьи инфицируются случайно, при этом они окрашиваются в красный цвет. Инфицированные муравьи излечиваются (опять становятся синими) либо спонтанно, сами по себе, через некоторый интервал времени, либо при встрече с доктором. Черные муравьи (доктора) не меняют свой цвет — предполагается, что доктора умеют уберечь себя от заражения.

Описание модели

Модель содержит два активных объекта. Один моделирует поведение мура­вья (Ant), другой — корневой объект Model, моделирует среду, в которой перемещаются агенты-муравьи. Он включает множество муравьев с именем ants (реплицированный экземпляр активного объекта Ant). Число этих объ­ектов задается параметром numAnts и в процессе функционирования модели является статическим, не изменяется. Вначале все муравьи располагаются случайно в прямоугольнике с координатами Х от 0 до maxX, Y от 0 до maxY, их начальные скорости по координатам в любом направлении случайны и

ограничены величиной maxVelocity. Величины maxX, maxY И maxVelocity также являются параметрами модели. Перемещение муравьев происходит синхронно при получении периодического сигнала из среды.

Активный объект Ant (муравей)

Каждый муравей выступает в двух ролях: как движущийся в замкнутом про­странстве объект, избегающий столкновений с другими объектами той же природы, и как инфицированный либо неинфицированный объект. Поэтому

модель муравья содержит два независимых стейтчарта, каждый из которых описывает свою активность. Стейтчарт main служит для описания правил движения муравья, стейтчарт health описывает состояние его здоровья: как инфицированного либо неинфицированного объекта (рис. 15.9).

Переменные. У муравья шесть переменных. Переменные х и у — текущие координаты объекта, vx, vy — его текущие скорости по координатам, пере­менная obsticie содержит указатель на того муравья, который стоит на пу­ти движения данного муравья. Переменная m будет указывать на объект, включающий данный экземпляр муравья.

То, что скорость муравья определена парой составляющих по координатам X и Y, дает возможность работать с ней как с вектором, определяя и направ­ление движения муравья. Координаты х, у и скорости vx, vy — это вещест­венные переменные, которые при порождении каждого объекта класса Ant принимают значения, установленные в поле Начальное значение окна свойств каждой из этих переменных. Для того чтобы расположить муравьев в начальный момент равномерно в поле анимации, начальное значение их координат задано как реализация случайной величины, равномерно распре­деленной от 0 до mахX для х и до maxY для у. Чтобы начальные скорости всех порожденных экземпляров этого класса были бы случайными как по направлению, так и по величине, начальные значения скоростей по коор­динатам также задаются как реализации равномерно распределенной слу­чайной величины: uniform) -maxVelocity, maxVelocity)

Переменная obsticie (препятствие) имеет тип Ant — это встретившийся на пути данного муравья другой муравей, мешающий его движению. Когда ни­кто движению данного муравья не будет мешать, значение этой переменной будет равно null — пустому объекту. Очевидно, что именно это значение нужно установить в поле Начальное значение данной переменной.

Еще одна переменная с именем m указывает на объект Model, включающий все экземпляры муравьев. С помощью этого указателя можно изменять гло­бальные переменные — переменные родительского объекта. Ее начальное значение установлено как null, а в поле Код инициализации окна Код этого активного объекта значение переменной установлено так:

m = (Model)getOwner();

В поле Дополнительный код класса активного объекта Ant включена функ­ция v, которая возвращает абсолютную скорость муравья. Эта функция ис­пользуется при вычислении нового положения каждого муравья.

Параметры. Параметры maxvelocity, maxX и maxY активного объекта Ant очевидны — они устанавливают максимальную скорость по координатам и границы движения муравья в поле анимации. Параметр turnAngle опреде­ляет, на какой угол должен повернуть муравей после того, как он встретит препятствие, чтобы избежать повторного столкновения. Параметр stopTime определяет, на сколько времени должен муравей замереть при такой встре­че. Все эти параметры при экспериментах с моделью желательно устанавли­вать глобально, из корневого объекта, поэтому конкретные значения их внутри класса Ant можно установить произвольно (т. е. просто считать ну­левыми).

Параметры doctor и trace определяют для каждой реализации объекта класса Ant, будет ли она соответственно доктором и нужно ли отслеживать для нее траекторию движения. Эти параметры булевы, и их можно устано­вить в true в каждом объекте с некоторой вероятностью, определяющей процент объектов с данным свойством в популяции. Это удобно сделать с помощью функции randomTrue(p), которая возвращает булевское значе­ние true с вероятностью р. В данной модели значения параметров doctor и trace установлены соответственно так:

randomTrue(0.1) randomTrue(0.03)

Это означает, что в нашей модели около 10 % всех муравьев при их порож­дении будут докторами и примерно у 3 % муравьев будет отслеживаться их траектория движения.

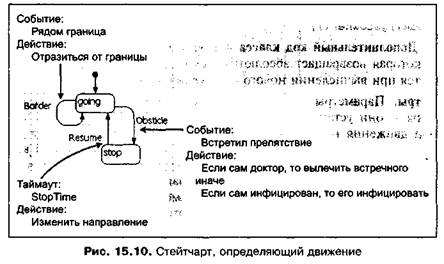
Стейтчарты. Стейтчарт main определяет движение муравья (рис. 15.10). Он имеет два состояния: состояние движения going и состояние ожидания stop. В состоянии движения муравей находится до тех пор, пока не про­изойдет одно из двух событий — либо он натолкнется на границу простран­ства, в котором живут муравьи, либо перед ним возникнет препятствие.

Событие приближения муравья к границе области при его движении возни­кает, если муравей подошел близко к границе и его движение направлено к этой границе. Именно это определяется булевой функцией border, вызов которой стоит в поле Событие перехода Border стейтчарта. Сама функция

border определена в поле Дополнительный код класса окна Код активного объекта Ant. Если это событие произошло, то муравей изменяет направле­ние своей скорости и переходит в состояние stop (останавливается).

Функция border вычисляется исполнительной системой AnyLogic, когда объект находится в состоянии going только при "толчке" извне. Такой тол­чок инициируется при вызове функции setModified () у данного активного объекта. В описываемой модели это периодически делается из корня — ак­тивного объекта Model. Так реализуется синхронное поведение всей системы агентов.

Другой переход из состояния going в состояние stop может произойти по событию, если муравей наталкивается на препятствие — другого муравья. Сигналом этого служит его собственный непустой указатель на препятствие (obsticle). При этом переходе выполняется следующее действие: если дан­ный муравей — доктор, то он вылечивает встретившегося муравья (посылая стейтчарту health встретившегося муравья сигнал "cure"). Если же данный муравей не доктор и к тому же инфицирован, то он заражает встретившего­ся муравья с некоторой вероятностью (посылая его стейтчарту health сиг­нал "afflict").

В состоянии stop муравей находится фиксированное время, определенное параметром stopTime, после чего он возвращается в состояние движения. При этом он меняет направление своего движения на угол turnAngle, также являющийся параметром класса. Для чего пересчитываются составляющие скорости по осям.

Стейтчарт health отслеживает здоровье муравья (рис. 15.11), он имеет два состояния, здоровое ok и инфицированное bad.

Находясь в здоровом состоянии, муравей может инфицироваться либо слу­чайно (это моделируется переходом со случайным значением таймаута с экспоненциальным распределением), либо после получения сигнала "Инфицирован" ("afflict") от встретившегося ему на пути инфицированно­го муравья.

Обратный переход из инфицированного в здоровое состояние происходит либо сразу, если данный муравей доктор, либо через некоторое случайное время, либо при получении сигнала "Вылечен" ("cure") от встретившегося ему на пути доктора.

При входе в состояние ok выполняется действие m.numOk++, что приводит к увеличению числа питок модели, показывающего количество всех здоро­вых муравьев популяции. Вспомним, что переменная m указывает на вклю­чающий всех муравьев объект Model, а питок — переменная этого активного класса. При выходе из состояния выполняется действие m.numOk--. Анало­гичные действия выполняются при входе и выходе из состояния bad для из­менения глобального числа инфицированных муравьев.

Корневой активный объект Model

Класс Model включает две переменных, питок и numAfflicted, роль которых ясна. Первая переменная содержит текущее число здоровых, вторая — те­кущее число инфицированных муравьев. Эти переменные модифицируют муравьи популяции, переходя от состояния ok в состояние bad и обратно. Корневой класс включает также набор муравьев (реплицированный экземп­ляр активного объекта Ant) и статический таймер stepTimer. Параметры класса следующие:

- numAnts — число муравьев в популяции;

- maxX, maxY, maxVelocity, turnAngle И stopTime — ЭТО одноименные па­раметры движения муравьев, которые для всех экземпляров класса Ant, включенных в класс Model, мы сможем устанавливать и менять из класса

Model;

- visionAngle — параметр, определяющий угол зрения муравья, исполь­зуемый при обнаружении им препятствия;

- step — шаг по времени, через который все экземпляры класса Ant син­хронно меняют свое состояние.

Все параметры класса Model имеют заданные значения, например значения mахX и maxY установлены как 600. Это означает, что муравьи будут двигаться в квадрате 600x600, со значением х и у от 0 до 600.

Множество муравьев, которое включено в модель, названо ants. В окне свойств любого объекта, включенного как экземпляр в класс другого актив­ного объекта, его параметры могут быть либо оставлены такими же, какими они были установлены при определении этого класса, либо они могут быть изменены. Измененные значения параметров включенного объекта выделя­ются жирным шрифтом.

В данной модели параметры doctor и trace были определены в классе Ant

Как randomTrue(0.03) И randomTrue (0.1) соответственно. При включении

в класс Model они остались такими же и для объекта ants. Все другие зна­чения параметров объекта ants выделены жирным шрифтом. Это значит, что они имеют новые значения. Действительно, хотя в поле Значение параметров объекта ants записаны те же имена (maxX, maxY, maxvelocity, turnAngle и stopTime), что и имена этих параметров в классе Ant, но здесь они определены в области действия имен класса Model, поэтому это именно одноименные параметры класса Model, а не параметры класса Ant.

Статический таймер stepTimer циклически при каждой его активизации через step единиц времени вызывает функцию update, которая определена в поле Дополнительный код класса окна Код класса Model. Именно эта функция определяет "жизнь" модели на каждом шаге, изменяя состояние всех объектов модели, т. е. модель является синхронной. В ней выполняются два шага. Сначала для каждого муравья определяется возможное препятст­вие, если он слишком близко подошел к какому-нибудь другому муравью и тот находится в области его видимости. Это проверяется с помощью булевой функции checkobsticle, определенной в этом же поле. Если данный мура­вей натолкнулся на препятствие, то его параметр obsticle будет теперь ука­зывать на данное препятствие, а исполнительная система получает инфор­мацию о том, что его состояние изменено (инициируется функция setModified у данного муравья).

Второй шаг функции update состоит в том, чтобы изменить положение всех тех муравьев, которые не стоят из-за наличия препятствия перед ними (если их параметр obsticle на данном шаге равен null). Каждый муравей про­двигается вперед в направлении, которое определяется его вектором скоро­сти (vx, vy), а исполнительная система также получает информацию о том, что его состояние изменено (вызывается функция этого агента setModified). Муравьи, таким образом, продвигаются вперед каждый шаг

времени step. Такой прием синхронной организации движения агентов ока­зывается с вычислительной точки зрения намного более эффективным, чем моделирование движения каждого агента с помощью дифференциальных уравнений. В то же время выбором шага синхронного продвижения времени в модели можно получить достаточно адекватную модель движения коллек­тива агентов в пространстве.

Анимация модели

Анимация представляет движение всех агентов в двумерном пространстве. Кроме положения муравья, показывается также его состояние здоровья (инфицирован или нет) и состояние движения (ожидает он у препятствия или нет). Состояние здоровья представляется цветом геометрических эле­ментов, выступающих в роли муравьев. У каждого из них в окне динамиче­ского значения цвета указано:

doctor? Color.black: health.isStateActive(health.ok)? Color.blue: Color.red

В соответствии с таким определением, цвет будет установлен черным (color.black), если булева переменная doctor данного объекта имеет зна­чение истина (иными словами, если данный муравей — доктор). Если нет, то цвет будет установлен в синий (color.blue), если в стейтчарте health активно состояние ok (т. е. если данный муравей здоров). Наконец, если все предыдущие условия не выполняются, цвет будет выбран красным.

Муравей в состоянии ожидания показывается кружком (поэтому в его поле Видимость стоит obsticle!= null), а в состоянии движения показывается отрезком прямой (поэтому в поле Видимость отрезка стоит obsticle). Пе­риодический поворот отрезка, представляющего муравья, на ±0.3 радиана относительно его основного направления движения с помощью функции Math, sin (getTime() * 2) * 0.3

создает эффект колебаний в процессе движения. Развернутое изображение муравья показывается (поле Видимость кружка), если у него нет на пути препятствия, т. е. если указатель obsticie пуст. Свернутое изображение, соответственно, показывается, если препятствие есть. Чтобы свернутое изо­бражение представлялось сегментом кольца, в анимации введен отрезок прямой, закрывающий часть изображения кольца.

Движение некоторых муравьев в анимации (тех, у которых параметр trace установлен в true) отслеживается — траектория их движения некоторое время отрисовывается. Для того чтобы нарисовать траекторию этих не­скольких муравьев, изображение траектории (и фиксирующего круга-прицела) определяется у всех, но в поле ее видимости установлен параметр trace, т. е. видна будет траектория только у некоторых — у тех, у которых значение переменной trace истинно. Траектория движения муравья задает­ся ломаной с именем path. Перерисовка траектории муравьев, если они не

стоят перед препятствием, осуществляется запуском кода, находящегося в поле Код обновления окна Код в анимации класса Ant, каждый раз, как изображение в поле анимации обновляется:

if(' trace && obsticle == null) {

path.setPoint(0, x, у);

for(int i=path.getPoints()-1; i>=l; i--)

path.setPoint(i, path.getPointX(i-l), path.getPointY(i-1)); } Построенная модель открыта для внесения дополнений и изменений.

Заключение

Агентный подход применяется для решения проблем во всех тех случаях, когда именно индивидуальное поведение объектов является существенным в системе, а интегральные характеристики и динамика всей системы выво­дятся из этих индивидуальных поведений. С помощью агентов можно модели­ровать рынки (агент представляет потенциального покупателя со своей ис­торией, возрастом и родом занятий), конкуренцию компаний на рынке (агент — компания со своим капиталом, стратегией и бизнес-процессами), динамику населения (агент — семья, житель или избиратель со своими по­литическими предпочтениями, уровнем образования, местом проживания) и многое другое.

Глава 16