Оценивание коэффициентов моделей

 

       После того, как найдены параметры моделей p и q, необходимо перейти к оцениванию коэффициентов моделей ВР, т.е. определить вектора 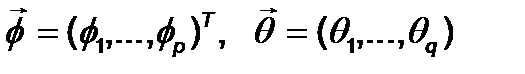  и дисперсию белого шума σ² по результатам наблюдений. Необходимо отметить, что идентификация порядка модели и оценивание ее коэффициентов неизбежно перекрываются. Например, можно оценить коэффициенты модели, которая оказалась более сложной, чем ожидалось, поэтому здесь нужно решить, что именно поддается упрощению. В этом случае процедура оценивания играет роль идентификации.

    Для оценки параметров модели может быть использован метод моментов, сущность которого сводится к замене выборочными оценками, в частности, выборочными средним, дисперсией и АКФ их теоретических аналогов и решением полученных уравнений для получения оценок неизвестных параметров. Кроме того, альтернативой методу моментов может служить метод максимального правдоподобия (МП), который также может применяться при оценке параметров моделей ВР.

 

    Модель AR (p)

    Для оценки коэффициентов модели AR (p), описываемой выражением (2.1), можно применить уравнения Юла-Уолкера. При использовании этого метода в модели AR (p) оцениванию подлежат коэффициенты 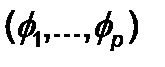  и σ². Для нахождения оценок этих коэффициентов необходимо иметь систему из (р + 1) совместно определенных уравнений. Уравнения Юла-Уолкера обычно записываются в матричном виде следующим образом

                                                      (2.35)

где Γ _р - ковариационная матрица; γ _р = [γ(1),..., γ(p)] ^T.

    При замене ковариаций γ(j), j = 0,..., p соответствующими выборочными оценками    получим систему уравнений оценок Юла-Уолкера

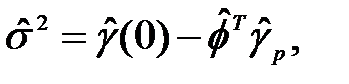                                                (2.36)

 

где в отличие от уравнений (2.35) записаны выборочные оценки соответствующих величин.

    В случае, когда  > 0, матрица    является несингулярной для каждого m = 1, 2,..., поэтому уравнения (2.36) можно переписать в следующем виде

 

                                                                    (2.37)

                                                (2.38)

 

где 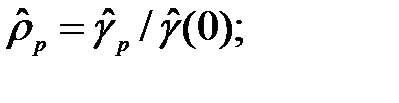  - выборочная корреляционная матрица размером р * р.

    В частности, для модели AR ( 1) коэффициент 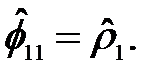  Для модели AR (2) уравнения Юла-Уолкера (2.37) при использовании выборочных корреляций принимают вид

,

 

где   - означает j -ый авторегрессионный параметр процесса порядка р.  

    Из последнего уравнения получаем 

 

  

  

    Аналогично можно определить оценки коэффициентов для моделей авторегрессии более высоких порядков. 

    Отметим, что моментные оценки коэффициентов, которые (подобно ) получаются путем приравнивания теоретических и выборочных моментов, имеют более высокую дисперсию, чем при использовании альтернативных методов, в частности, метода МП. 

Однако оценки коэффициентов, найденные через уравнения Юла-Уолкера, имеют приблизительно такое же распределение, как соответствующие МП-оценки. В случае большой выборки из модели AR (р) распределение оценок коэффициентов подчиняется приблизительно нормальному закону [4]

  

где n  - объем выборки. 

 

    Модель МА(q)

    В этом случае для оценки коэффициентов модели МА (q) обычно используется метод МП. Имеются два подхода к оцениванию функции правдоподобия (ФП) для модели МА (q) [1]:

1. В первом случае предполагается, что начальные значения шума   a_t = 0 для t ≤ 0. По существу, эти величины, необходимые для вычисления ФП, получаются рекурсивным способом из модели, начиная от a ₁ = X_t и a ₂ = X ₂ - θ₁ a ₁. Такой прием можно охарактеризовать как условный метод правдоподобия, а получающиеся оценки являются условными МП-оценками.

2. Во втором случае начальные значения шума a_t, t ≤ 0 рассматриваются как дополнительные коэффициенты модели, которые оцениваются совместно с другими параметрами. Такой подход трактуется как точный   метод правдоподобия. МП-оценки, получаемые этим методом, предпочтительней условных МП-оценок, но требуются более интенсивные вычисления. При достаточно большой выборке наблюдений указанные приемы получения МП-оценок оказываются близки друг к другу.

    Рассмотрим модель МА (1), которая имеет вид

X_t = a_t + θ a_{t -1}, t = 1,…, T.

    При зарегистрированных значениях x ₁,..., x_T последовательно выражаем a ₁,..., a_T    через наблюдения и величину   a ₀ (ненаблюдаемую) следующим образом

a ₁ = X ₁ – θ a ₀,

a ₂ = X ₂ – θ a ₁ = X ₂ – θ(X ₁ – θ a ₀),

...

a _T = X_T – θ a_{T – 1}.

    Максимизация по θ условной ФП, соответствующей наблюдаемым значениям x ₁,..., x_T при фиксированном значении a ₀, эквивалентна минимизации суммы квадратов 

Q (θ) = a ₁² + a ₂² +... + a_T ²,

которая является нелинейной функцией от θ. Переход от максимизации к минимизации обусловлен свойством обратимости процесса МА (q). Для поиска минимума этой суммы квадратов приходится использовать итерационные методы оптимизации, которые, в свою очередь, требуют задания начального предварительного значения параметра θ. 

    Начальные стартовые значения могут быть получены из условия, что первые q автокорреляций модели МА (q) не равны нулю и выражаются через коэффициенты модели, как это показано в приведенном выше равенстве (2.18). Данное выражение для ρ₁, ρ₂,..., ρ _q через θ₁, θ₂,.., θ _q дает q  уравнений с q неизвестными. Предварительные оценки коэффициентов θ можно получить, подставив в (2.18) выборочные значения автокорреляций и решив получающиеся нелинейные уравнения. Однако итоговое (после итераций) оптимальное значение θ зависит от неизвестной величины a ₀, что затрудняет интерпретацию результатов. Последнее облегчается в случае, если выполняется условие обратимости θ < 1, и при этом значение θ существенно меньше 1.

    Действительно, при выполнении этого условия можно просто принять a ₀ = 0. Эффект от такой замены истинного значения a ₀ на нулевое быстро убывает, так что сумма квадратов, получаемая в предположении a ₀ = 0, может служить хорошей аппроксимацией для суммы в случае истинного значения a ₀ при большом количестве наблюдений. Такие же доводы справедливы и для модели MA (q) при q > 1: в этом случае можно принять, что a ₀ = a _-1 =... = a _{- q +1} = 0. Для получения более точной аппроксимации в ряде статистических пакетов предусмотрена процедура так называемого обратного прогноза (ретро-прогноза), при котором процесс итераций включает в себя и оценивание значений a ₀, a _-1,..., a _{- q +1}.

 

    Модель ARMA (p, q)

    При оценке коэффициентов этого процесса нужно учитывать его двойственность, как сформированного из авторегрессионной модели и процесса скользящего среднего. В этом случае оцениванию подлежат p + q + 1 параметров   

    При использовании метода моментов процесс нахождения коэффициентов разбивается на два этапа. На первом шаге оцениваются коэффициенты   регрессионной составляющей c помощью выборочных оценок ковариаций. Используя уравнение (2.29), которое может быть преобразовано к виду      

и заменив в последнем выражении ковариации их оценками, получим  систему из р уравнений с неизвестными коэффициентами  . В результате решения приходим к оценке вектора коэффициентов .

    На втором шаге применение аналогичного приема с заменой ковариаций их оценками в уравнении, подобном приведенному выше, даст оценку вектора коэффициентов θ.

    При гауссовом белом шуме для оценки коэффициентов модели ARMA (p, q) можно  также использовать метод МП [2,7]. Общая схема его применения такова. Выражаем значения АКФ процесса через коэффициенты модели, формируем ковариационную матрицу, записываем функцию правдоподобия для имеющейся выборки данных, решаем (как правило, численно) систему уравнений правдоподобия относительно оценок коэффициентов.

    Отметим, что большинство используемых пакетов дает возможность визуализировать ряд, построить АКФ и ЧАКФ, получить оценки параметров модели. 

 

Проверка адекватности

    Построение модели ВР представляет собой итеративный процесс, который начинается с идентификации модели и оценки параметров. После этого необходимо оценить адекватность модели путем проверки выполнения допущений модели. Основное допущение заключается в том, что значения { a_t } являются белым шумом. Иначе говоря, величины a_t   - некоррелированы, имеют нулевое среднее и постоянную дисперсию. Для любой оцениваемой модели остатки  являются оценками ненаблюдаемых значений белого шума a_t. Вследствие того, что исследование ряда остатков представляет собой этап оценки параметров, проверка адекватности обычно содержится на оценочной фазе обычного пакета по анализу ВР.   

    Для проверки нормальности остатков необходимо построить их гистограмму (или гистограмму стандартизированных остатков /σ _a ²) и сравнить ее со стандартным нормальным распределением.

 С целью проверки постоянства дисперсии нужно рассмотреть график остатков. Для проверки того, что остатки являются (приближенно) белым шумом, необходимо вычислить и построить выборочные АКФ и ЧАКФ ряда остатков. Статистическая незначимость остатков имеет место в ситуации, когда значения АКФ и ЧАКФ не выходят из зоны неопределенностей. Таким образом, адекватность модели подразумевает, что отклонение реальных данных от модельных описывается нормальным законом, а корреляция отклонений (остатков) является незначимой.