При подгонке модели ВР по имеющимся данным необходимо решить три задачи:
1) идентифицировать модель, т.е. получить некоторую информацию о конкретных значениях параметров p и q, определяющих вид модели А RMA (р, q);
2) оценить параметры модели, т.е. найти такие значения величин
ф 1 ,..., ф p и θ1,..., θ q в модели
Xt = ф 1 Xt -1 + …+ ф p Xt -p + at + θ1 а t – 1 +…+ θ q а t – q,
которые в определенном смысле являются лучшими для наблюдаемого ВР;
3) оценить адекватность модели, т.е. проверить выполнение допущений модели.
Идентификация модели
При анализе ВР самые важные шаги для идентификации и построении модели основаны на доступных данных. Эти шаги требуют хорошего понимания процессов, определяющих ВР, и, в частности, характеристик АКФ ρ k и ЧАКФ ф kk. На практике вместо самих функций ρ k и ф kk используются их оценки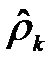 
и 
. Таким образом, при идентификации модели наша цель сводится к сопоставлению выборочных оценок АКФ и ЧАКФ с их теоретическими аналогами для рассматриваемых моделей ВР. Методы идентификации, по существу, представляют собой процедуры, которые применяются к данным наблюдений для выявления типа моделей с целью использования последних в дальнейших исследованиях, например, при прогнозировании. Поскольку модель А RMA (р, q) включает в себя как частные случаи модели А R (р) и MA (q), то начнем идентификацию с модели авторегрессии.
Модель авторегрессии
Для определения порядка р модели авторегрессии можно использовать два подхода:
· посредством частной автокорреляционной функции (ЧАКФ);
· с помощью информационного критерия Акайка (Hirotugu Akaike).
Рассмотрим вначале первый метод. ЧАКФ временного ряда является функцией его АКФ и служит полезным средством для определения порядка модели AR (p). Отметим, что АКФ определяется ковариацией между значениями процесса, отстоящими на τ шагов по времени друг от друга. Однако на поведение процесса AR (p) статистически влияет не только его значение в момент, равный τ шагов назад, но и все промежуточные значения процесса между моментами t и t – τ. ЧАКФ исключает влияние всех промежуточных значений ряда и показывает лишь "чистую" взаимосвязь между моментами t и t – τ.
Методика расчета ЧАКФ изложена выше (п.1.4), где было показано, что частная автокорреляция между Х t и Х t + k определяется коэффициентами уравнения регрессии, связывающего переменную Х t + k с k задержанными переменными Х t + k - 1, Х t + k - 2,..., Х t.
Оценка 
есть выборочная ЧАКФ переменной Xt на лаге 1; оценка 
- выборочная ЧАКФ переменной Xt на лаге 2; оценка 
третьего уравнения - выборочная ЧАКФ переменной Xt на лаге 3 и т.д.
Отсюда следует, что ЧАКФ при лаге 2 определяет дополнительный вклад Xt - 2 в модель AR (1), равную Xt = 
1,1 Xt - 1 + a 1 t. ЧАКФ при лаге 3 дает дополнительный вклад Xt - 3 в модель AR (2) и т.д. Вследствие этого для модели AR (p) выборочная ЧАКФ при лаге р не должна быть равна нулю, но значение 
должно быть близким к нулю для всех j > p. Такое свойство можно использовать для определения порядка p, в частности, выборочная ЧАКФ модели AR (p) обладает следующими свойствами:
· 
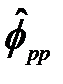сходится к 
при увеличении объема наблюдений до бесконечности;
· стремится к нулю для всех k > p.
В итоге, можно сказать, что для модели AR (p) выборочная ЧАКФ обрывается на лаге р.
При втором подходе укажем, что существует несколько информационных критериев для определения порядка р модели AR (p). Все критерии основаны на отношении правдоподобия. Например, хорошо известный информационный критерий Акайка определяется как [Brockwell, с.173 такой формулы у него не нашел]
AIC = (-2)* T -1 ln Q + 2* T -1 l,
где Q - функция отношения правдоподобия; l - число параметров; T - объем выборки.
Для гауссовых моделей AR (p) критерий AIC сводится к виду
где 
- оценка максимального правдоподобия дисперсии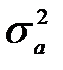 
процесса at.
На практике вычисляются величины AIC (l) при l = 0,1,..., P, где P - заранее определенное положительное целое число, и выбирается такой порядок модели p, при котором достигается минимальное значение AIC (l).
Модель скользящего среднего
АКФ является полезной при идентификации порядка рассматриваемой МА -модели. Порядок МА -процесса легко определяется по его выборочной АКФ, т.е. временной ряд Xt описывается моделью МА (q), если оценка АКФ ρ q ≠ 0, но значение ρ l = 0 при l > q. ЧАКФ обычно оказывает меньшую помощь при идентификации МА -модели вследствие быстро затухающей формы этого коэффициента.
Смешанная модель
В рассмотренных выше моделях AR (p) и MA (q) вид АКФ и ЧАКФ дает возможность идентифицировать параметры этих процессов. Напомним, что процесс { Xt } описывается моделью MA (q), если соответствующая АКФ срезается до нуля на лаге q. С другой стороны, ЧАКФ процесса { Xt } обрывается на лаге р при описании последнего моделью AR (p).
Процесс ARMA (p, q) объединяет свойства моделей AR (p) и MA (q), поэтому у модели ARMA (p, q) при лагах τ > q действие ее компонента в виде скользящего среднего прекращается, и оказывает влияние только авторегрессионная составляющая. Вследствие этого при τ > q поведение АКФ процесса ARMA (p, q) аналогично характеру изменений АКФ процесса AR (p), т.е. с увеличением лага постепенно стремится к нулю.
С другой стороны, рассмотрение частных автокорреляций приводит к следующему: в связи с тем, что ЧАКФ процесса AR (p) становится равной нулю при лагах τ > р, то на поведение ЧАКФ модели ARMA (p, q) при τ > р влияет его составляющая в виде MA (q). В итоге, это приводит к тому, что ЧАКФ процесса ARMA (p, q) постепенно сходится к нулю.
В [ 2 Бокс,т.1, с.196] для смешанной модели указано, что АКФ такого процесса, содержащая компонент авторегрессии порядка р и составляющую скользящего среднего порядка q, после первых (q – р) задержек представляется в виде суммы экспонент и затухающих синусоид. С другой стороны, ЧАКФ этой модели приближенно описывается суммой экспонент и затухающих синусоид после (p – q).
Однако для смешанной модели АКФ и ЧАКФ не дают достаточной информации с точки зрения нахождения параметров р и q. В частности, визуальный анализ графиков АКФ и ЧАКФ не позволяет однозначно определить параметры р и q модели ARMA (p, q). Трудности еще более возрастают при замене АКФ и ЧАКФ их оценками, полученными из наблюдений.
В программных пакетах предлагаются различные способы идентификации параметров. Например, в широко известном пакете Statistica при рассмотрении такой задачи указывается, что решение не является простым и требуется основательно поэкспериментировать с альтернативными моделями. Тем не менее, большинство встречающихся на практике ВР можно с достаточной степенью точности аппроксимировать одной из пяти основных моделей, которые можно идентифицировать по виду АКФ и ЧАКФ. Отметим, что число параметров каждого вида невелико (меньше 2), поэтому нетрудно проверить альтернативные модели.
1. Один параметр авторегрессии (p): АКФ - экспоненциально убывает; ЧАКФ - имеет резко выделяющееся значение для лага 1, нет корреляций на других лагах.
2. Два параметра авторегрессии (p): АКФ имеет форму синусоиды или экспоненциально убывает; ЧАКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах.
3. Один параметр скользящего среднего (q): АКФ имеет резко выделяющееся значение на лаге 1, нет корреляций на других лагах. ЧАКФ экспоненциально убывает.
4. Два параметра скользящего среднего (q): АКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах. ЧАКФ имеет форму синусоиды или экспоненциально убывает.
5. Один параметр авторегрессии (p) и один параметр скользящего среднего (q): АКФ экспоненциально убывает с лага 1; ЧАКФ - экспоненциально убывает с лага 1.
