По существу, модель представляет собой математическое представление действительности и может быть использована для различных целей:
1. Она дает полезное описание данных, включающее моделирование как систематической составляющей, так и необъясненной части (компонент ошибки).
2. Модель помогает подтвердить или отвергнуть теоретические соотношения, предлагаемые априори. Кроме того, она может облегчить сравнение между различными наборами данных.
3. Систематическая часть модели уменьшает трудности при построении точечного прогноза, а описание необъясненной части помогает вычислить интервальный прогноз.
Рассмотрим примеры имитации приведенных выше моделей.
Модель AR (1)
Примем начальное значение Х 0=0; величину дисперсии белого шума (при нулевом среднем) равной σ2=0,2; значение коэффициента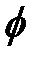 
=0,8. Модель в этом случае описывается уравнением
Xt = 0,8 Xt - 1 + at.
Разыгранный ряд из 100 значений показан на рис.2.9. На рис.2.10 приведены АКФ и ЧАКФ, откуда можно заключить (по наличию единственного выброса на графике ЧАКФ), что ряд, приведенный на рис.2.9, описывается моделью AR (1).
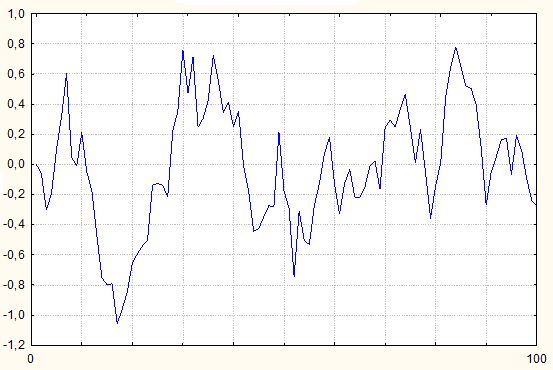
Рис.2.9. Разыгранный процесс AR (1)
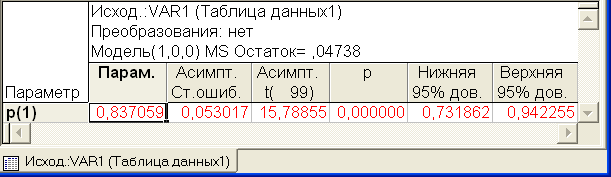
Рассчитанный коэффициент 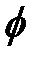смоделированного процесса приведен в табл.2.3, который равен величине 0,84, что весьма близко к принятому при розыгрыше значению 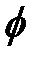=0,8.
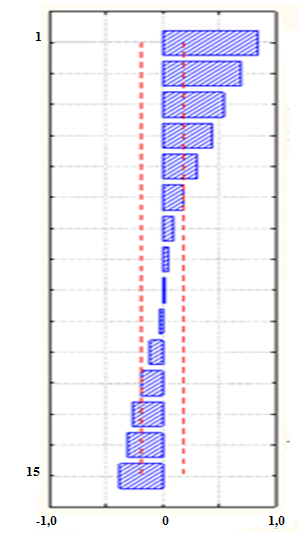
Рис.2.10. АКФ (слева) и ЧАКФ (справа) разыгранного процесса
Таблица 2.3 Оценки коэффициента модели AR (1)
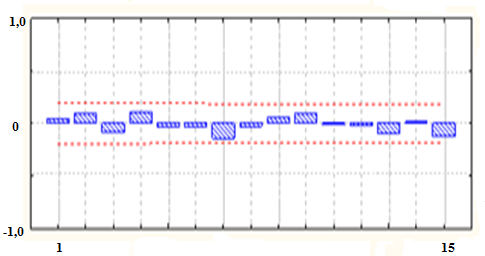
При адекватности разыгранных данных и предполагаемой модели остатки должны быть некоррелированы и распределены по нормальному закону. На рис.2.11.а, б показаны графики корреляции остатков и их распределения (на специальной диаграмме), откуда следует вывод об их некоррелированности и описания нормальным законом. (Далее с целью сокращения не будем приводить такие графики).
На рис.2.12 показан график модели AR (1) вида
Xt = - 0,8 Xt - 1 + at,
которая отличается от предыдущей лишь знаком при коэффициенте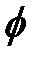 
.
а)
б)
Рис.2.11 Графики АКФ остатков (а) и их распределения (б)
Отметим, что для процесса AR (1)
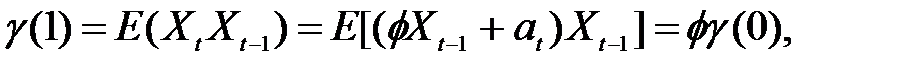
поэтому ρ(1) = γ(1) / γ(0) = .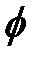
Таким образом, при значениях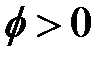 
(близких к 1) между соседними данными наблюдается сильная положительная корреляция, что обеспечивает более гладкий характер поведения траекторий ряда по сравнению с процессом белого шума. В противном случае, при 
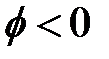, процесс авторегрессии обладает менее гладкими реализациями, так как в этой ситуации имеет место тенденция чередования знаков последовательных наблюдений. Из сравнения рис.2.9 и 2.12 видно, что при одинаковой модели, но с разными коэффициентами характер изменения рядов различен.
Рис.2.12. График модели AR (1) при 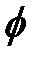= - 0,8
Соответствующие этой модели графики АКФ и ЧАКФ приведены на рис.2.13.
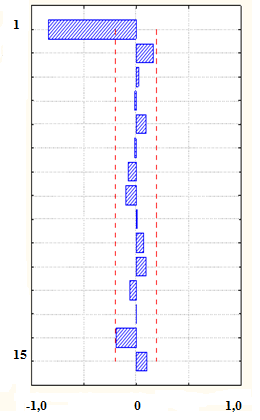
Рис.2.13 АКФ (слева) и ЧАКФ (справа) процесса AR (1)
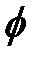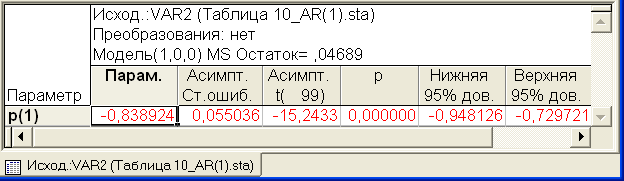
Как видно из сопоставления графиков АКФ двух рядов, различающихся только знаком при коэффициенте, расчетные значения автокорреляций при единичном лаге равны: ρ1(1)~ 1=0,841; ρ2(1)~ 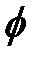1= - 0,839 (сравни табл. 2.3 и 2.4).
Таблица 2.4 Оценки коэффициента модели AR (1)
Модель AR (2)
В этом случае модель описывается выражением
Xt = ф 1 Xt - 1 + ф 2 Xt - 2 + at.
При имитации этого ряда параметры были приняты равными: ф 1 = ф 2 = 0,25; параметр at распределен по нормальному закону с нулевым средним и единичной дисперсией.
На рис.2.15 приведен график разыгранного ряда, а рассчитанные АКФ и ЧАКФ - на рис.2.16.
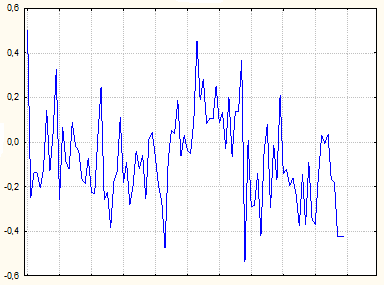
Рис.2.16 График разыгранного процесса AR (2)
Отметим, что дать однозначный ответ по виду АКФ и ЧАКФ о предполагаемой модели трудно, но, тем не менее, два значимых выброса на графике ЧАКФ свидетельствуют в пользу процесса AR (2).
а)
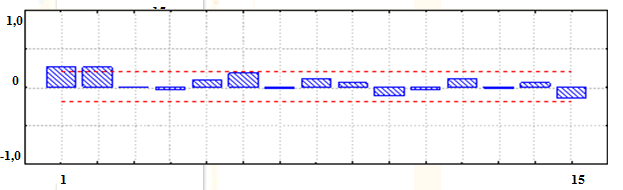
б)
Рис.2.16. АКФ (а) и ЧАКФ (б) процесса AR (2)
В табл.2.5 приведены оценки коэффициентов модели AR(2), которые близки к принятым при моделировании.
Таблица 2.5 Оценки коэффициентов модели AR (2)
Из последних графиков видно, что результаты имитации не противоречат модели AR (2).
Перейдем к имитации процессов, описываемых моделями скользящего среднего.
Модель MA (1)
Эта модель описывается уравнением Xt = at - θ at -1. При имитации примем: θ = 0,8; параметр at распределен по нормальному закону с нулевым средним и единичной дисперсией. Результаты имитации этого процесса приведены на рис.2.17.
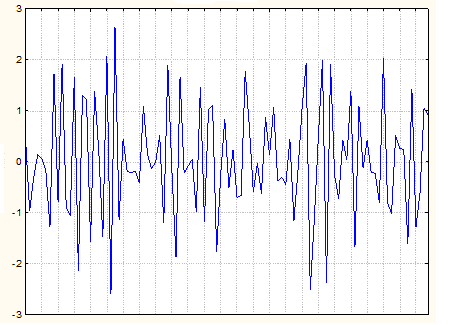
Рис.2.17. График разыгранного процесса МА (1)
Соответствующие графики АКФ и ЧАКФ показаны на рис. 2.18, откуда по единственному значимому выбросу АКФ можно сделать предположение о принадлежности разыгранного процесса модели МА (1).
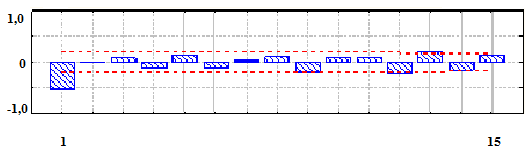
а)
б)
Рис.2.18 АКФ (а) и ЧАКФ (б) процесса МА (1)
В табл.2.6 приведена оценка коэффициента θ модели МА (1), которая близка к значению, принятому при моделировании.
Таблица 2.6 Оценка коэффициента модели МА (1)
Рассмотрим имитацию того же процесса, отличающегося только знаком при коэффициенте, т.е. здесь примем θ = - 0,8. Графики разыгранного процесса (рис.2.19), АКФ и ЧАКФ (рис.2.20) и таблица результатов расчета (табл.2.7) приведены ниже.
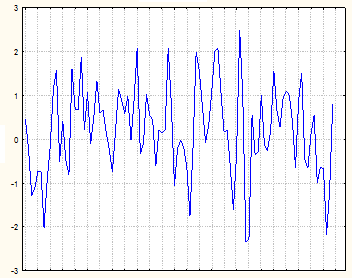
Рис.2.19. График разыгранного процесса МА (1)
а)
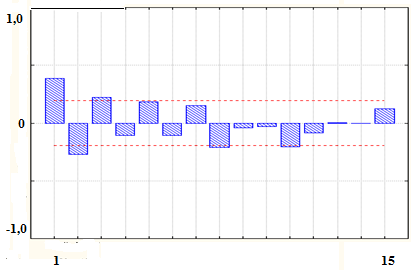
б)
Рис.2.20. АКФ (а) и ЧАКФ (б) процесса МА (1)
Таблица 2.7 Оценка коэффициента модели МА (1)
Как следует из приведенных результатов, разыгранный процесс не противоречит модели МА (1).
Перейдем к модели скользящего среднего второго порядка.
Модель МА(2)
Эта модель описывается уравнением Xt = at + 1,0 at -1 - 0,5 at -2. При имитации примем: θ1 = 1,0; θ2 = -0,5; параметр at распределен по нормальному закону с нулевым средним и единичной дисперсией. Результаты имитации этого процесса приведены на рис.2.21, а результаты расчета параметров модели МА (2) - в табл.2.8.
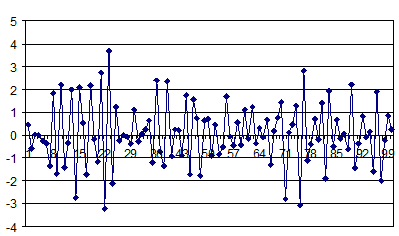
Рис.2.21. График разыгранного процесса МА (2)
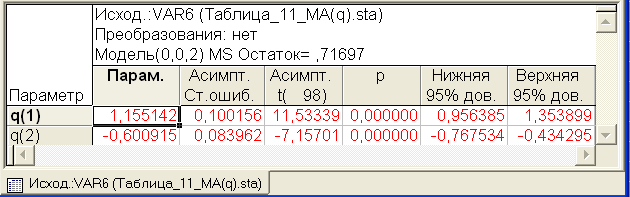
Как видно из табл.2.8, рассчитанные по разыгранным данным оценки параметров θ1 =1,15 и θ2 =-0,60 незначительно отличаются от величин, принятых при моделировании. Для сокращения материала здесь уже не приводятся графики АКФ и ЧАКФ.
Таблица 2.8 Оценка коэффициентов модели МА (2)
Перейдем к имитации процесса, который описывается смешанной моделью первого порядка.
Модель ARMA ( 1,1 )
Эта модель описывается уравнением Xt = 0,5 Xt - 1 + at - 0,5 a t - 1. Разыгранные 100 значений этого ряда приведены на рис.2.22.
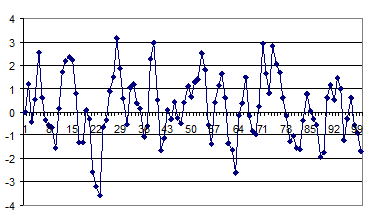
Рис.2.22. Разыгранный ряд ARMA ( 1,1 )
Соответствующие разыгранному ряду графики АКФ И ЧАКФ приведены на рис.2.23, однако для смешанной модели этой информации недостаточно для принятия решения.
а)
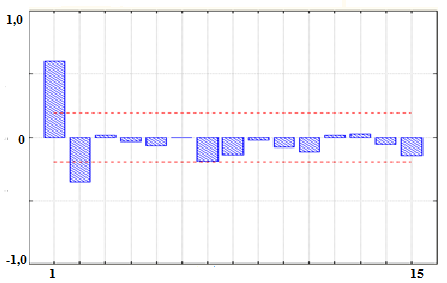
б)
Рис.2.23 - АКФ (а) и ЧАКФ (б) разыгранного ряда
В литературе [8 Носко] даются некоторые рекомендации по идентификации модели с помощью АКФ и ЧАКФ. В частности, в табл.2.9 указан характер поведения корреляционных функций.
Таблица 2.9 Характер поведения АКФ и ЧАКФ
| Модель | АКФ | ЧАКФ |
ARMA(1,1);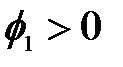 
| Экспоненциальное убывание с лага 1 | Осциллирующее убывание с лага 1 |
ARMA(1,1); 
| Осциллирующее убывание с лага 1 | Экспоненциальное убывание с лага 1 |
| ARMA(p,q) | Осциллирующее или прямое убывание с лага q | Осциллирующее или прямое убывание с лага p |
В табл.2.10 приведены результаты расчета параметров разыгранных данных, описываемых моделью ARMA (1,1).
Таблица 2.10 Результаты расчета
Как видно из табл.2.10, найденные оценки параметров близки к использованным при розыгрыше.
