Здесь обсудим три вида представления смешанной модели А RMA (р, q). Указанные формы служат трем различным целям, а знание таких преобразований может привести к лучшему пониманию процесса, описываемого моделью А RMA (р, q). Первая форма этой модели определяется выражением (2.24), которое при помощи операторов сдвига назад становится равным ф (В) Xt = θ(В) at.
Для других представлений используем следующий подход. При двух заданных многочленах вида 
можно получить следующие соотношения
(2.32)
Например, если 
то имеем
.
Из двух последних равенств получаем, что 
Используя тот факт, что Bc =с для любой постоянной (значение постоянной инвариантно во времени), приходим к соотношениям
AR - представление
С использованием второго из выражений (2.32) модель А RMA (р, q) может быть записана как
(2.33)
Это представление показывает зависимость текущего значения Xt от прошлых величин Xt – i. Коэффициенты {π i } являются π-весами модели А RMA. Поскольку вклад задержанных величин Xt – i в Xt уменьшается с увеличением номера i, весовые коэффициенты π должны спадать до нуля при увеличении i. Модель А RMA (р, q), обладающая таким свойством, является обратимой.
Для "чистой" AR -модели θ(B) = 1, поэтому π(В) = ф (В). Таким образом, π i = 0 для i > p, и модель является обратимой. Для других А RMA -моделей достаточное условие обратимости состоит в том, что все нули полинома θ(B) превышают по модулю единицу.
Например, рассмотрим модель МА (1) вида Xt = (1 + θ1 B) at. Нуль полинома первого порядка 1 + θ1 B равен В = - 1/ θ1. Вследствие этого модель МА (1) является обратимой, если 
, что эквивалентно неравенству 
Из AR -представления в уравнении (2.33) следует, что обратимая А RMA -модель определяет ряд Xt как линейную комбинацию текущего значения помехи и взвешенного среднего прошлых значений ряда. Веса спадают экспоненциально для более удаленных прошлых значений.
МА -представление
Модель А RMA (р, q) с использованием первого из выражений (2.32) может быть записана в виде
(2.34)
где среднее значение μ = E (Xt) = ф 0 / (1 – ф 1 - …- ф p).
Это представление ясно показывает воздействие прошлых значений помехи at - i (i > 0) на текущее значение Xt. Коэффициенты ψ i определяют функцию импульсного отклика модели А RMA (р, q). Для слабо стационарных рядов коэффициенты ψ i экспоненциально спадают при увеличении i. Это очевидно, так как влияние помехи at - i на переменную Xt должно уменьшаться со временем. Таким образом, для стационарной модели А RMA помеха at - i не оказывает постоянного воздействия на ряд. Если ф 0 ≠ 0, тогда МА -представление имеет постоянный член, равный среднему значению Xt, т.е. ф 0 / (1 – ф 1 - …- ф p).
Отметим следующие свойства модели А RMA.
1. Если процесс имеет постоянное математическое ожидание μ, то он описывается моделью А RMA (р, q) вида
.
2. При E (Xt) = μ процесс стационарен, если все корни уравнения 
(z) = 0 лежат вне единичного круга z ≤ 1.
3. Для стационарного процесса А RMA (р, q) существует эквивалентный ему процесс МА (∞) вида
Последнее выражение можно записать как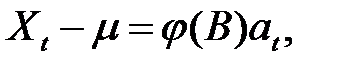 
где 
4. Если все корни уравнения θ(z) = 0 лежат вне единичного круга z ≤ 1 (условие обратимости), то существует эквивалентное представление процесса Xt в виде процесса авторегрессии бесконечного порядка AR (∞)
которое можно записать в виде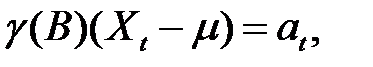 
где 
Из приведенных соотношений следует, что стационарный процесс А RMA (р, q) всегда можно аппроксимировать процессом СС достаточно высокого порядка, а при выполнении условия обратимости - процессом АР высокого порядка.
