Модель скользящего среднего

Глава 2 Модели стационарных временных рядов

 

2.1 Авторегрессионная модель. 1

2.2 Модель скользящего среднего. 10

2.3 Смешанные модели. 16

2.4 Три формы представления смешанной модели. 21

2.5 Подгонка моделей стационарных временных рядов. 24

2.5.1 Идентификация модели. 25

2.5.2 Оценивание коэффициентов моделей. 32

2.5.3 Проверка адекватности. 36

2.6   Имитация моделей стационарных временных рядов. 37

2.7 Примеры стационарных временных рядов. 52

 

Многие процедуры прогнозирования в явной или неявной форме основаны на моделях ВР. Вследствие этого в данной главе проводится анализ моделей стационарных ВР для ознакомления и дальнейшего изучения возможностей построения прогнозных оценок. При ограниченном числе доступных наблюдений часто формируется параметрическая модель для описания процесса ВР. Класс моделей ARIMA, введенный Боксом и Дженкинсом еще в 1970-х гг., представляет собой мощный аппарат прогнозирования и является основой многих фундаментальных идей при анализе ВР. Такие модели иногда называются моделями Бокса- Дженкинса. В главе рассматриваются вначале  авторегрессионная модель AR (р)и модель скользящего среднего МА (q), а затем   смешанная модель ARMA (р, q), которая включает указанные выше модели как специальные случаи. Анализируются свойства каждого вида процессов и приводятся иллюстративные примеры. Материал главы основан на работах (. [из Chatf.2,3.1.4; Wei,p.38, еще Brockwell,p.54. Носко]

......) и примерах автора.

Авторегрессионная модель

 

Рассмотрим авторегрессионную (АР) модель порядка р, уравнение для которой можно записать в виде

                                         (2.1)

В выражении (2.1) величины ф ₁,..., ф_р используются для обозначения набора весовых коэффициентов; a_t определяет белый шум с нулевым средним и дисперсией σ², т.е. a_t ~ WN (0,σ²).

Модель (2.1) называется процессом авторегрессии порядка р или сокращенно AR (p) (autoregressive process). Такое название объясняется тем, что линейная модель вида

связывающая зависимую переменную F с множеством независимых переменных x ₁, х₂,..., х _r    плюс случайная ошибка e обычно называется моделью регрессии: говорят, что F регрессирует на x ₁, х₂,..., х _r.   В равенстве (2.1) переменная Х _t регрессирует на свои предшествующие значения, поэтому модель называется авторегрессионной. Следовательно, АР    процесс можно охарактеризовать как модель, в которой текущее значение ряда в момент t    выражается через конечное число прошлых значений (систематическая зависимость от прошлых значений) и величину возмущения a_t, не зависящую от прошлого.  

    Для упрощения примем, что С ov (X_{t – s}, a_t) = 0 для всех s > 0; при этом говорят, что случайные величины a_t образуют инновационную последовательность, а величина a_t называется инновацией  для наблюдения в момент времени t. Такая терминология объясняется тем, что наблюдаемое значение ряда в момент t получается как линейная комбинация р предшествующих значений этого ряда плюс не коррелированная с этими значениями случайная составляющая a_t.  

       Для изучения свойств ВР воспользуемся оператором сдвига назад (1.10), действие которого на ВР дает значение ряда в предыдущий момент времени. Последовательное применение оператора сдвига р раз определяет значение ВР в момент времени на р периодов раньше, что позволяет ввести степень сдвига оператора

       С помощью оператора сдвига модель (2.1) можно записать в эквивалентной форме

которая после введения оператора авторегрессии    принимает вид                                            

                                                                              (2.2)

где   - полином В  порядка р.

    Формально в методологии Бокса-Дженкинса процесс AR (p) можно представить как прошедший через фильтр белый шум. Передаточная функция такого фильтра определяется как 

    Соответствующее характеристическое уравнение имеет  вид

                          z^p – ф ₁ z^{p -1} - ф ₂ z^{p -2} - …- ф_р = 0.                          (2.3)

    В случае, если все р корней уравнения (2.3) находятся вне окружности единичного радиуса (все корни по модулю меньше единицы), то процесс AR (p) является стационарным. 

Получим основные соотношения для модели AR (p). Умножив левую и правую части (2.1) на Х _{t - k}, получим 

 Взяв математическое ожидание от обеих частей последнего равенства, приходим к рекуррентному соотношению для автоковариаций (напомним, что Ea_t = E Х _t = 0, E (Х _{t - h} a_t) = 0 при h > 0 и E (Х _t a_t) = s ² _a)

(2.4)

 

Поделив все члены в (2.4) на D Х _t, находим, что автокорреляции удовлетворяют аналогичному соотношению

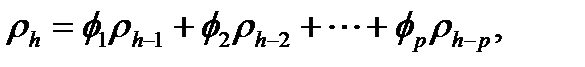                                                           (2.5)

 а дисперсия процесса может быть записана в виде   

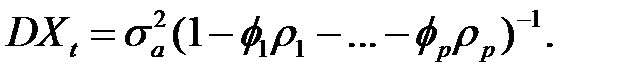
    Наибольший интерес в практических задачах играют модели AR (1) и AR (2).

    Из выражения (2.1) получаем для процесса первого порядка AR (1) уравнение в виде

                                  (2.6)

На рис.2.1 представлена реализация процесса AR (1) c  = 0,8;    X ₀ =0, рассчитанная по уравнению (2.6) при a_t ~ N (0, 1).

 

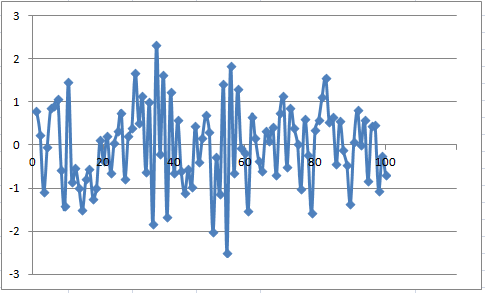
Рис.2.1. Реализация процесса AR (1) при = 0,8

 

Выражению (2.6) соответствует характеристическое уравнение        z -  = 0 с единственным корнем z  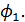= При  < 1 обеспечивается стационарность процесса.

    Для дисперсии модели AR (1)  получаем

Var (X_t) = σ _a ² / (1 - ф ₁²), 

откуда вытекает требование, чтобы ф ₁² < 1. Такое требование следует из того факта, что дисперсия случайной переменной ограничена и неотрицательна. Следовательно, слабая стационарность процесса AR (1) включает условие: - 1 < 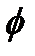₁ < 1.    

    Для АКВФ имеем

γ _h  = ф ₁ γ _{h – 1}     для h > 0.

    C учетом дисперсии процесса для АКФ получим

ρ _h = ф ₁ ^h для h > 0.                               (2.7)

    При условии  и, следовательно, стационарности процесса АКФ экспоненциально спадает двумя различными путями, зависящими от знака ф ₁. Если  0 < ф ₁ < 1, тогда все автокорреляции - положительны;  если  -1 < ф ₁ < 1, тогда величины автокорреляций носят знакопеременный характер. Рассчитанные по уравнению (2.7) зависимости АКФ от лага показаны на рис.2.2.

 

    

              а)                                                            б)

Рис.2.2. Автокорреляционная функция для процесса AR (1)

(а - ф ₁ = 0,8; б - ф ₁ = - 0,8)

Как видно из рис.2.2, АКФ с увеличением лага спадает экспоненциально (при положительном коэффициенте) или попеременно меняя знак (при отрицательном  коэффициенте).

Для ЧАКФ процесса AR (1) из выражения (1.5) следует

 

Здесь, похоже, нужен индекс h.

Следовательно, ЧАКФ процесса AR(1) имеет положительный или отрицательный выброс в зависимости от знака ф ₁. Кроме того, ЧАКФ становится равной нулю (обрывается) при значениях k > 1.

Заметим, что рассмотрение авторегрессионных ВР ограничивается так называемыми каузальными (вызванными какой-либо причиной, от английского слова: causal) процессами, в которых наблюдаемому ряду разрешено зависеть от настоящих и прошлых значений других переменных. Иначе говоря, время распространяется только в одном направлении - вперед. Если, например, разрешить параметру ф    превышать единицу для процесса AR (1), то ряд (2.6) будет иметь совершенно иной характер. В действительности, можно найти стационарную последовательность, которая удовлетворяет (2.6) при , позволив X_t   зависеть от  будущих значений a_t, однако для данных, составляющих ВР, такое предположение считается нереальным. В любом случае стационарный процесс AR (1) при 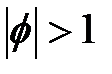   можно выразить как такой же процесс при  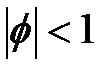  и такими же свойствами второго порядка (дисперсия, моменты), но основанный на другой временной последовательности помехи. Таким образом, ничего не изменяется при снятии ограничения 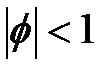. В ситуации,   когда          ф = 1, стационарное решение отсутствует. [из Chatf.2,3.1.4; Wei,p.38, еще Brockwell,p.54.]

    Из выражения (2.1) для модели AR (2) получаем

                         X_t = ф ₁ X_{t - 1} + ф ₂ X_{t - 2} + a_t.                         (2.8)

На рис.2.3 представлена реализация процесса AR (2) с ф ₁=1,2;      ф ₂= - 0,35, рассчитанная по уравнению (2.8) при a_t ~ N (0, 1).

 

Рис.2.3. Реализация процесса AR (2)

 

    Передаточная функция и характеристическое уравнение для этой модели, соответственно, имеют вид

W (z) = z ² / (z² – ф ₁z  – ф ₂), 

                               z ² – ф ₁ z  – ф ₂ = 0.                                (2.9)

    Процесс AR (2) является стационарным только в том случае, если оба корня уравнения (2.9) находятся внутри окружности единичного радиуса. Решением этого уравнения являются характеристические корни модели AR (2), которые определяются по формуле

                                                                (2.10)

    Обозначим характеристические корни через ω₁ и ω₂. Если оба корня - действительные числа, то характеристическое уравнение модели может быть разложено на множители и преобразовано к виду

z ² – ф ₁ z  – ф ₂= (1 - ω₁ В) (1 – ω₂ В).

    В случае если подкоренное выражение в уравнении (2.10) оказывается меньше нуля, т.е. ф ₁² + 4 ф ₂  < 0, то ω₁ и ω₂ являются комплексными числами. Таким образом, необходимые условия для стационарности процесса AR (2) независимо от того, являются ли корни действительными или комплексными, сводятся к следующим [Wein,3.1.16. p.40]:

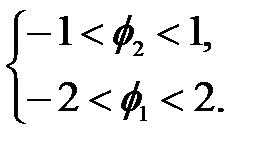                                                                  (2.11)

При этом для действительных корней условия стационарности (2.11) становятся равными 

                                                                   (2.12)

Из выражения (2.5) для АКФ модели AR ( 2) получим

                 ρ _k = ф ₁ρ _{k -1} + ф ₂ρ _{k -2} для k  > 0.                           (2.13)

    В частности, при лаге, равном 1, АКФ удовлетворяет уравнению

ρ₁ = ф ₁ ρ₀ + ф ₂ρ_-1 = ф ₁+ ф ₂ρ₁.

    Вследствие этого для стационарного процесса AR (2) имеем:

    ρ₀ = 1; ρ₁ = ф ₁/ (1 - ф ₂); ρ _k = ф ₁ρ _{k -1} + ф ₂ρ _{k -2} для k  ≥ 2.

    На рис.2.4 показаны рассчитанные АКФ модели AR(2 ) при разных значениях коэффициентов: рис.2.4.а - ф ₁ = 1,2; ф ₂ = - 0,35; рис.2.4.б - ф ₁ = 0,6; ф ₂ = - 0,4. В последнем случае корни характеристического уравнения являются комплексными [0,36 +4 (-0,4) = -1,24 < 0], поэтому здесь  изменение АКФ отличается от рис. 2.4.а. 

                                                             а)                                                                 

                                                             б)

Рис.2.4. Автокорреляционная функция модели AR (2) 

 

    Частные автокорреляционные функции для процесса AR (2) могут быть определены с учетом равенств (1.5) и (2.13) таким образом:

 

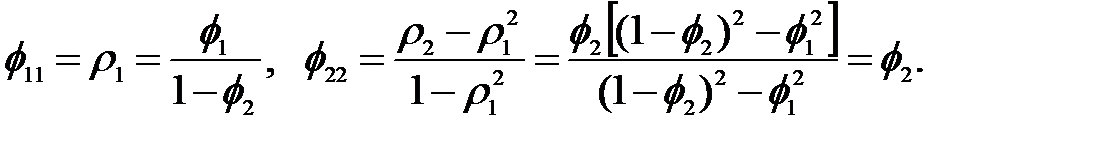
    Для следующей ЧАКФ имеем

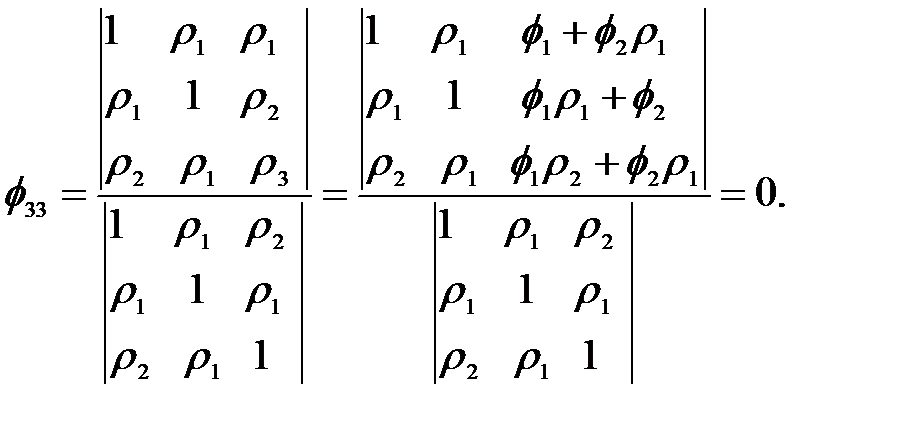                                  (2.14)

    Равенство нулю выражения (2.14) следует из того факта, что последний столбец числителя представляет собой линейную комбинацию первых двух столбцов. Аналогично, можно показать, что ф _kk = 0 для         k ≥ 3, следовательно, ЧАКФ процесса AR (2) срезается после лага, равного двум.

Модель скользящего среднего

    Модель скользящего среднего (СС) (Moving Average - MA) является полезной при моделировании различных ВР в финансовой деятельности. Эта модель предполагает, что в ошибках модели в предшествующие периоды сосредоточена информация по всей предистории ряда. Модель СС порядка q - MA (q) - запишем в виде

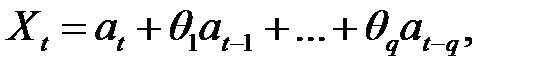                                                (2.15)

где символы q ₁,..., q _q используются для обозначения конечного набора весовых параметров.

 Соотношение (2.15) определяет процесс МА(q), который представляет собой линейную комбинацию текущего и прошлых значений шума a_t.  

Используя оператор сдвига назад В, можно записать для процесса (2.15) эквивалентное выражение

                                             (2.16)

В равенстве (2.16) θ(В) определяет собой полином В  порядка q.

Из формулы (2.16) следует, что процесс СС можно трактовать как выход Х _t  линейного фильтра с передаточной функцией q (B), на вход которого поступает белый шум a_t. Как видно из соотношения (2.15), процесс Х _t при любом n  ≥ q определяется конечным числом значений a_t, а _{t – 1} ,...,  а _{t – q} белого шума, поэтому такой фильтр принято называть фильтрами с конечной памятью. При   n ≥ q   процесс является стационарным со средним значением E { Х _t } = 0.

Необходимо отметить, что в некоторых источниках, включая и основополагающую книгу Бокса-Дженкинса [1974г.], в равенстве типа (2.15) стоит знак минус, по-видимому, на том основании, чтобы выражение θ(В) имело форму, аналогичную равенству (2.2) для ф (В) в случае АР процесса AR (p). Здесь нет принципиальной разницы между двумя обозначениями, но знаки у параметров θ - противоположные, что может явиться причиной недоразумений при сравнении формул из различных источников или анализе результатов компьютерных  расчетов [Chatf.,2, point. 3.1.2]м.б.не указывать здесь?      

    На значения параметров модели MA (q) обычно накладывается условие обратимости. Сущность этого условия может быть объяснена следующим образом. Положим, что { a_t } и { a_t * } -  независимые случайные процессы и . Тогда можно показать, что два процесса МА (1), определяемые как    X_t = a_t + θ а _{t – 1} и    X_t = a_t * + θ^-1 а* _{t – 1}, имеют одинаковые АКФ. Таким образом, полином θ(В) не является единственным, который характеризуется этой АКФ. Как следствие, сама выборочная АКФ не служит в качестве единственной оценки процесса МА (1) без наложения определенных ограничений. Для разрешения этой неопределенности обычно требуется, чтобы корни полинома θ(В) находились вне единичного круга. Отсюда следует, что выражение (2.15) можно переписать в следующем виде

                                                         (2.17)

для некоторых постоянных π _j таких, что

    Другими словами, можно инвертировать (обратить) функцию, описывающую ряд a_t, в ряд X_t   и восстановить a_t   по настоящим и прошлым значениям X_t  в виде сходящейся суммы. Отрицательный знак у коэффициентов π _j  в выражении (2.17) устанавливается из условия, что процесс СС конечного порядка может быть записан как АР процесс бесконечного порядка. Таким образом, условие обратимости процесса MA (q): корни θ(х) лежат вне единичного круга является зеркальным отражением условия стационарности процесса AR (p): корни (х) лежат вне единичного круга. На основании свойства обратимости можно придти к заключению, что стационарный процесс AR (p) конечного порядка соответствует процессу СС   бесконечного порядка, а обратимый процесс MA (q) конечного порядка – АР   процессу бесконечного порядка [Wei,p.57].

Далее из (2.15) следует, что АКВФ имеет вид

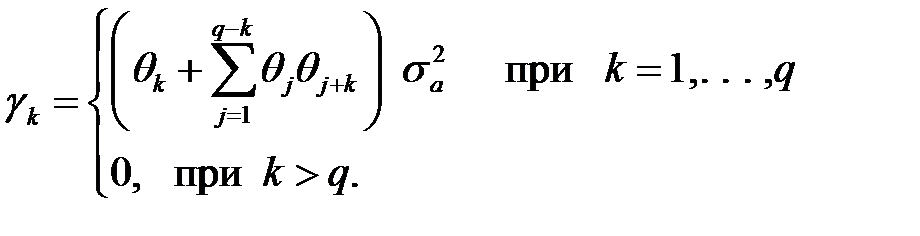
Из последнего равенства для дисперсии процесса получим

                        

(напомним, что ввиду четности функции γ _k достаточно ее определить при k ³ 0). Для АКФ следует очевидное представление

                                       (2.18)

Таким образом, для модели МА(q) автокорреляция обрывается на задержке q, и конечная протяженность автокорреляции является характерным свойством этой модели. В случае, если r ₁,..., r _q известны, то q   уравнений (2.18)  можно в принципе разрешить относительно параметров q ₁,..., q _q. В этой модели статистическая связь между наблюдениями сохраняется в течение q единиц времени (т.е. протяженность памяти процесса равна q).

Такого типа временные ряды соответствуют ситуации, когда некоторый показатель находится в равновесии, но отклоняется от него вследствие последовательно возникающих непредсказуемых событий.  

Полученный результат принципиально различает процессы AR (р) и МА (q): если у процесса AR (р) при τ → ∞ (монотонно или колебательно) АКФ постепенно стремится к нулю, то у процесса МА (q) при τ = q АКФ обрывается и в последующем остается равной нулю.

Процесс скользящего среднего напрямую связан с теоремой Вольда  (1.1). В теореме доказано, что стационарный процесс, являющийся чисто недетерминированным (purely indeterministic), т.е. процесс не содержит детерминированного компонента, всегда выражается в виде (2.15). Формально любой стационарный недетерминированный ВР можно представить в виде теоремы Вольда, выражение для которой при нулевом среднем значении становится равным

                                                                           (2.19)

где ψ₀ = 1; 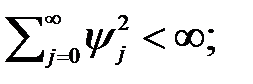  { a_t } – чисто случайный процесс с нулевым средним и постоянной дисперсией σ².

    Выражение (2.19) определяет собой процесс МА (∞), который часто называют представлением Вольда для изменяющегося процесса. Иногда используют и другие термины, в частности, линейный процесс или обобщенный линейный процесс. Однако необходимо отметить, что последние дефиниции применяются в ситуации, когда { a_t } не являются независимыми, а являются некоррелированными, или когда суммирование в (2.19) проводится в диапазоне от - ∞ до + ∞. Естественно, что при нормально распределенных величинах { a_t } нулевая корреляция включает в любом случае и независимость компонентов, поэтому наряду с указанными выше терминами используется такое определение как гауссовский линейный процесс. На практике декомпозиция Вольда имеет ограниченный характер. Даже при линейном процессе представление стохастического процесса в виде МА (∞) требует бесконечного числа параметров, которые невозможно оценить по конечной выборке данных. Обычно при поиске модели, отвечающей принципу экономичности, необходимо ограничиваться всего лишь несколькими параметрами. 

Рассмотрим модели СС первого и второго порядков. Обобщение на модели более высоких порядков можно выполнить по аналогии. Для модели МА (1) из (2.15) получаем

                                      X_t = a_t + θ₁ а _{t – 1}.                                     (2.20)

    Дисперсия этой модели выражается как

Var(X_t) = σ _a ² + θ₁² σ _a ² = (1 + θ₁²) σ _a ², 

где использовалось допущение о независимости a_t   и а _{t – 1} .

    При определении АКВФ для модели МА (1) вначале умножим (2.20) на X_{t – k}, что дает 

X_{t – k} X_t = X_{t – k} a_t  + θ₁ X_{t – k} а _{t – 1} , 

а затем возьмем операцию математического ожидания, после чего получим

γ₁ = θ₁² σ_a², γ _k  = 0 для k  > 1.

    Для АКФ элементарные преобразования дают

                                                                (2.21)

    Таким образом, для модели МА (1) при лаге, равном 1, АКФ не равна нулю, но при больших значениях лагов АКФ обращается в нуль. Другими словами, можно сказать, что АКФ модели МА (1) обрывается на лаге, равном 1, т.е. модель МА (1) не "помнит", что произошло в  момент, соответствующий двум временным интервалам назад! 

    Для ЧАКФ в этом случае с использованием выражений (1.5) и (2.21) после ряда преобразований приходим к следующему результату

    Таким образом, 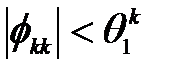, и в ЧАКФ преобладающим членом является затухающая экспонента. Отметим взаимность процессов AR (1) и МА (1). В то время как АКФ процесса МА (1) обрывается после задержки, равной единице, АКФ процесса AR (1) экспоненциально затухает с ростом задержки. И, наоборот, при экспоненциальном затухании ЧАКФ процесса МА (1) ЧАКФ процесса AR (1) обрывается после задержки, равной единице.   

    Модель МА (2) по аналогии выражается следующим образом

                                     X_t = a_t + θ₁ а _{t – 1}  + θ₂ а _{t – 2}.                            (2.22)

    АКФ для этой модели определяется как                       

ρ₁ = (θ₁ + θ₁ θ₂) / (1 + θ₁² + θ₂²),

                                         ρ₂ = (θ₂) / (1 + θ₁² + θ₂²),                           (2.23)

ρ _k = 0 для k  > 2.

    В этом случае АКФ обрывается после лага, равного 2. Это свойство обобщается и на  МА- модели других порядков, например, для модели МА (q) при лаге, равном q, АКФ не равна нулю, но ρ _k = 0 для k  > q. Следовательно, ряд  МА (q) является линейно связанным со своими первыми, задержанными до лага, равного q, значениями, и является процессом с "конечной памятью".

    Точное выражение для ЧАКФ процесса МА (2) оказывается достаточно сложным, но главную роль в нем играет либо сумма двух экспоненциальных членов (если корни характеристического уравнения, соответствующего модели (2.22), действительны), либо затухающая синусоида (если корни характеристического уравнения комплексные).  

В качестве примера на рис.2.6 показаны смоделированные реализации процессов МА (1) при θ₁ = 0,5 и МА (2) при θ₁ = 0,5;          θ₂ = 1,0.

  а)      

                                                                                                                                                      

                                                                       б)

Рис.2.6. Реализация процессов МА (1) (а - θ₁ = 0,5) и МА (2) (б - θ₁ = 0,5; θ₂ = 1,0)

 

Смешанные модели

Моделями А R (р) и МА(q) за счет выбора их порядков р и q можно удовлетворительно описывать многие реальные процессы. Однако на практике такие процессы становятся чересчур громоздкими из-за необходимости применения моделей высокого порядка для адекватного описания динамической структуры данных. Для достижения большей гибкости в подгонке моделей к наблюдаемым временным рядам иногда бывает целесообразным объединить в одной модели и авторегрессию, и скользящее среднее. Решению этой задачи помогает рассмотрение смешанных моделей авторегрессии - скользящего среднего, т.е. моделей А RMA (р, q), которые имеют следующий вид                                  

X_t = ф ₁ X_{t -1} + …+ ф _p X_{t -p} +  a_t + θ₁ а _{t – 1}  +…+ θ _q а _{t – q}         (2.24)

или в другой эквивалентной форме через операторы

                                             ф (В) X_t = θ(В) a_t,                                 (2.25)

где ф (B), q (B) - операторы, определенные ранее для моделей А R (р) и МА(q).

    Кроме того, важность моделей А RMA (р, q) объясняется еще тем, что многие реальные данные могут быть описаны более экономично (это означает необходимость меньшего числа параметров) с использованием смешанных моделей А RMA (р, q), чем отдельными процессами с применением моделей А R (р) и МА(q).

    По выражению (2.25) можно сделать следующие выводы:

· ВР { X_t } является AR -процессом порядка р, т.е. AR (р), если θ(В)= 1 или ф (В) X_t = e_t, где e_t   подчиняется процессу скользящего среднего порядка q, т.е. e_t = θ(В) a_t;

·  ВР { X_t } является МА -процессом порядка q, т.е. MA (q), если     ф (В)= 1 или X_t = θ(В) b_t, где b_t подчиняется процессу авторегрессии порядка р, т.е. (В) b_t  = a_t.

    Таким образом, ф (В) X_t = θ(В) a_t.                                     

    Очевидно, что члены со скользящим средним в правой части (2.24) не оказывают влияния на условия стационарности процесса авторегрессии. Вследствие этого выражение (2.25) является стационарным процессом при условии, что все корни характеристического уравнения ф (В) = 0 лежат вне единичного круга. Аналогично, процесс является обратимым, если корни уравнения      θ(В) = 0 лежат вне единичного круга.

    Модель (2.24) может интерпретироваться как линейная модель множественной регрессии, в которой в качестве объясняющих переменных выступают прошлые значения самой зависимой переменной, а в качестве регрессионного остатка - скользящие средние из элементов белого шума. 

Для вывода АКВФ перепишем (2.24) в виде 

и умножим обе части последнего уравнения на X_{t - k}  

.

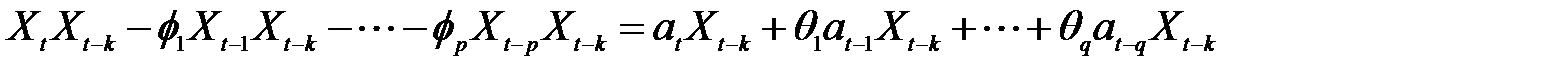    Теперь найдем математическое ожидание от обеих частей последнего выражения

Поскольку , получаем для АКВФ

              

Следовательно, АКФ модели А RMA (р, q) выражается следующим образом 

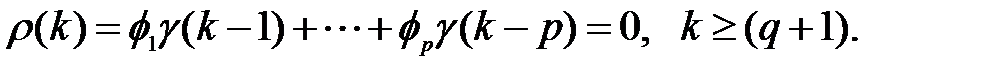                  (2.26) 

АКФ модели А RMA (р, q), определяемая уравнением (2.26), убывает после лага q, подобно AR -процессу, который зависит только от авторегрессионных параметров в смешанной модели. Однако первые q автокорреляций зависят как от параметров авторегрессионной модели, так и от характеристик модели СС. Такое различие оказывается полезным далее при идентификации модели.

Относительно ЧАКФ отметим следующее: поскольку процесс модели А RMA содержит как специальный случай процесс скользящего среднего МА (q), то ЧАКФ модели А RMA (р, q) представляет собой смесь убывающих экспонент или затухающих синусоид, зависящую от корней характеристических уравнений ф (B) = 0 и q (B) = 0.  

В простейшем случае для модели А RMA (1,1) из (2.24) имеем                                      

                                   X_t = ф ₁ X_{t - 1} +  a_t + θ₁ а _{t – 1}.               (2.27)

    Свойства модели А RMA (1,1) являются обобщением свойств модели А R (1) с некоторыми незначительными изменениями, вызванными воздействием компонента модели MA (1). Начнем с условия стационарности. Взяв  математическое ожидание от обеих частей уравнения (2.27), получим

E (X_t) - ф ₁ E (X_{t -1}) = E (a_t) + θ₁ E (а _{t – 1}).

    Так как E (a_i) = 0 для всех i, то среднее X_t равно

E (X_t) = 0.

    Последнее равенство обеспечивает слабую стационарность ряда. 

Умножив модель на а _t и взяв математическое ожидание, получим

E (X_t а _t) = ф ₁ E (X_{t -1} а _t ) + E (a_t²) + θ₁ E (а _t а _{t – 1}) = E (a_t²) = σ_a².    (2.28)

Рассмотрим АКВФ процесса А RMA (1,1). Для этого умножим (2.28) на (X_{t - h}), в результате чего имеем

X_t X_{t - h} = ф ₁ X_t X_{t - h} + a_t X_{t - h} + θ₁ X_{t - h} а _{t – 1}.

Для h = 1, взяв математическое ожидание и используя уравнение (2.28), приходим к такому результату

γ₁ - ф ₁γ₀ = θ₁ σ_a².

Полученный результат отличается от АКВФ для модели А R (1), для которой γ _h  - ф ₁γ _{h – 1} = 0. Однако для     h = 2 получаем, что   γ ₂  - ф ₁γ₁ = 0. Последнее выражение идентично АКВФ для модели А R (1). Фактически, одинаковые методы дают один и тот же результат в виде

                 γ _h  - ф ₁γ _{h – 1} = 0 для     h > 1.                    (2.29)

АКФ модели А RMA (1,1) с использованием предыдущих результатов определяется следующим образом

ρ₁ = ф ₁+ θ₁ σ_a² / γ ₀, ρ _h = ф ₁ρ _{h – 1} для h > 1,             (2.30)

где γ ₀ - дисперсия процесса  А RMA (1,1).

    Таким образом, АКФ модели А RMA (1,1) ведет себя во многом подобно изменению АКФ модели АR(1) за исключением того, что экспоненциальный спад начинается с лага h = 2, следовательно, АКФ процесса А RMA (1,1) не обрывается на любом конечном лаге. На рис.2.7 показана АКФ, рассчитанная по уравнению (2.30), при ф ₁=0,8; θ₁=0,5; σ_a² = 1; γ ₀ = 2.

Рис.2.7 Автокорреляционная функция модели ARMA (1,1)

 

Реализация модели ARMA (1,1) при ф ₁ = θ₁ = 1 приведена на рис.2.8.

Из общего вида модели (2.24) видно, что AR - и MA - модели являются частными случаями процесса А RMA (р, q), который с помощью оператора сдвига назад B   может быть записан в виде

                  (1 - ф ₁ В -... – ф _p В ^p) = (1 + θ₁ В+... + θ _q В ^q).         (2.31)

 

Рис.2.8. Реализация модели ARMA (1,1) 

 

    Полином в левой части равенства (2.31) представляет собой AR -полином; в правой - MA -полином модели. Необходимым требованием здесь является отсутствие общих факторов между AR и MA полиномами. В противном случае порядок (р, q) модели может быть понижен. Подобно "чистой" AR - модели AR -полином вводит характеристическое уравнение модели А RMA (р, q). В случае, если все решения характеристического уравнения по абсолютной величине меньше 1, то модель А RMA (р, q) - слабо стационарная.