Глава 2
2.1. Статическая оптимизация
Как уже отмечалось, при современных масштабах производства искусственного холода капитальные вложения в создание холодильных станций и расход энергии непосредственно на производство холода становятся очень большими. Сокращение их даже в доли процента за счет применения оптимальной конструкции оборудования или оптимального режима его работы может дать существенный экономический эффект. Использование методов математического моделирования применительно к анализу процессов, происходящих в холодильных установках или отдельных элементах, позволяет определить оптимальные условия их протекания, а также оптимально управлять ими при нарушении режимов работы или изменении входных факторов. Поэтому одной из задач, которую должен уметь решать бакалавр, является составление и использование алгоритма оптимального проектирования процесса или объекта алгоритма оптимального управления этим процессом или объектом.
В последнее время термин "оптимизация" получил очень широкое распространение, при этом употребление его часто недостаточно обосновано,
Как известно, оптимизация – это целенаправленная деятельность, заключающаяся в получении наилучших результатов при определенных условиях [6]. Это определение подчеркивает необходимость отыскания специфических методов, обеспечивающих безусловное получение наилучших результатов. Чтобы решать оптимизационные задачи, необходимо уяснить основные требования, предъявляемые к их постановке.
Прежде всего, постановка задачи оптимизации предполагает четкое выделение объекта оптимизации, независимо от того, что понимается под этим термином – конструкция машины или аппарата, режим осуществления технологического процесса и т.п.
Далее необходимо сформулировать цель оптимизации и разработать требования к объекту оптимизации. От правильности постановки этих требований часто зависит возможность решения задачи.
При формулировании цели необходимо учитывать, что правильной постановкой задачи оптимизации является нахождение оптимального значения только одной величины. Типичным случаем неправильной постановки задачи оптимизации является требование нахождения оптимальных значений нескольких величин одновременно, например "произвести максимальное количество холода при минимальном расходе энергии". Так как минимальный расход энергии равен нулю, то ни о каком максимальном количестве холода говорить нельзя. При правильной постановке задачи оптимизации можно говорить о "производстве максимального количества холода при заданном расходе энергии" или "о минимальном расходе энергии для производства заданного количества холода".
Встречающиеся в литературе упоминания о возможности одновременной оптимизации двух и более не связанных между собой величин сводятся, в конечном счете, к оптимизации также одной условной величины, которая определяется по следующему правилу:
где у – условная оптимизируемая величина; у i (i = 1, 2,.. .,п)– выходные факторы и параметры, по которым осуществляется оптимизация; a i (i = 1, 2,.. .,п) – «весовые» коэффициенты, сумма которых равна единице, оценивающие весомость (значимость) каждого выходного фактора или параметра в условной оптимизируемой величине у.
Так как значимость каждого выходного фактора или параметра (при отсутствии связи между ними) может быть установлена при таком подходе только на основе балльной (экспертной) оценки, эта методика неизбежно несёт печать субъективизма. Очевидно, что при наличии связи между выходными факторами и параметрами этот метод не применяется, так как уравнение связи между рассматриваемыми величинами позволяет определить единый критерий, учитывающий их взаимное влияние.
Для решения задачи оптимизации нужно располагать ресурсом оптимизации, под которым понимают свободу выбора значений некоторых управляющих факторов. Иными словами, объект оптимизации должен обладать определенными степенями свободы (управляющими воздействиями), которые позволяют менять его состояние в соответствии с теми или иными требованиями.
Кроме того, для правильной постановки задачи оптимизации интересующее качество объекта должно иметь количественную оценку. Количественная оценка оптимизируемого качества называется критерием оптимальности или целевой функцией.
Таким образом, для правильной постановки оптимизационной задачи необходимо соблюдение следующих условий: 1) требование оптимизации только одной величины; 2) наличие степеней свободы – управляющих воздействий у оптимизируемого объекта; 3) возможность количественной оценки оптимизируемой величины.
Постановка задачи оптимизации предполагает существование конкурирующих свойств объекта: количество продукции – качество продукции; количество продукции – расход сырья и т.п. Для любой энергетической системы, в том числе и для холодильной установки, включающей в свой состав теплообменные аппараты, такими конкурирующими свойствами являются капитальные затраты и расход энергии (эксплуатационные расходы). Действительно, увеличение температурных напоров в конденсаторе и испарителе приводит, с одной стороны, к уменьшению теплообменных поверхностей, а значит, к сокращению капитальных затрат, а с другой стороны, вызывает повышенный расход энергии, т.е. приводит к увеличению эксплуатационных расходов. Сокращение температурных напоров вызывает обратное явление. Наличие конкурирующих свойств особенно характерно при постановке оптимальной задачи с экономической оценкой. Выбор компромиссного решения и представляет собой процедуру решения оптимальной задачи.
Иногда требуется получить экстремальное значение какого-либо параметра, тогда конкурирующие свойства можно и не обнаружить. В этом случае речь идет об экстремальных свойствах самого объекта оптимизации, обусловленных природой протекающего в нем процесса.
Наиболее общей постановкой оптимизационной задачи служит выражение критерия оптимальности в виде экономической оценки. В общем виде это можно представить как
(2.1)
где R – критерий оптимальности; V – объем выпускаемой продукции (производительность); K – объем капитальных вложений; Э – эксплуатационные затраты; Q – качественные показатели продукта.
Конкретный вид уравнения (2.1) может быть различным в зависимости от постановки задачи, т.е. от того, что выбрано в качестве критерия оптимальности (сумма прибыли за определенный промежуток времени, себестоимость продукции (приведенные затраты), эффективность использования капитальных вложений и т.д.).
Не останавливаясь на рассмотрении экономических критериев оптимальности и методах их выбора, отметим, что формула (2.1) пригодна для определения оптимального стационарного режима, характерного для непрерывных производств, а также для периодических процессов, если анализ их экономических показателей охватывает большой период времени, включающий в себя несколько циклов периодического производства.
Наряду с задачами статической оптимизации (оптимизация стационарных режимов) существуют задачи оптимального управления при нестационарных режимах эксплуатации, т.е. задачи динамической оптимизации. Например, задача оптимального управления периодическим процессом за один рабочий цикл, обеспечивающего при заданном времени цикла максимальный выход продукции; задача пуска процесса и перевода его с одного режима на другой и т.д. В этом случае значение критерия оптимальности определяется не только положением, существующим в рассматриваемый момент времени, но и предысторией процесса. Поэтому для оценки эффективности в качестве критериев оптимальности в этом случае используются интегральные оценки – функционалы вида
(2.2)
где R – заданная функция параметров, определяющая состояние процесса в любой момент.
Режим работы холодильной установки определяется, как известно, температурами источников тепла – охлаждаемого объекта и окружающей среды. Последняя подвержена сезонным колебаниям, приводящим к периодическим изменениям режима работы холодильного оборудования. Поэтому, строго говоря, задача оптимизации режима работы холодильной установки является задачей динамической оптимизации, которая должна решаться с использованием в качестве критериев оптимальности функционалов вида (2.2).
Для осуществления целенаправленного поиска условий оптимума, т.е. условий, обеспечивающих достижение максимума или минимума (в зависимости от формулировки задачи) целевой функции, используются определенные математические методы. Ниже рассматриваются некоторые методы поиска экстремальных значений целевой функции, находящие себе применение при оптимизации холодильных установок.
2.1.1. Методы нахождения экстремума функции одной переменной
При решении оптимизационных задач обычно требуется найти экстремальное (максимальное или минимальное в зависимости от условий задачи) значение целевой функции. Для этого используют различные математические методы поиска экстремума. Все многообразие методов может быть разделено на две группы – аналитические и численные. Так как существует большое количество методов поиска экстремума функции, ниже рассматриваются лишь некоторые из них.
Метод классического анализа функций. Этот метод относится к аналитическим. Он может быть использован в случаях, когда известен аналитический вид зависимости оптимизируемой величины R от независимой (оптимизирующей) переменной x: (R = R (x)). Кроме того, для применения метода классического анализа функция R (x) должна быть непрерывна, по крайней мере, дважды дифференцируема, среди ограничений не должно быть неравенств и требований о положительности или целочисченности переменных.
Соблюдение всех этих требований позволяет найти аналитические выражения для производных оптимизируемой функции, использование которых позволяет формулировать необходимые и достаточные условия существования экстремума.
Условия существования экстремума у непрерывной функции R (x) при отсутствии ограничений на диапазон изменения переменной определяются из анализа первой производной 
. Функция R (x) может иметь экстремумы в тех точках оси x, где производная 
равна нулю или вообще не существует (графически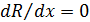 
означает, что касательная в этой точке параллельна оси х). Равенство производной нулю или ее отсутствие являются только необходимыми условиями существования экстремума, но не достаточными.
Как видно из рис.2.1, при значениях переменной, соответствующих x 2, и х 4, производная равна нулю, однако экстремума функций в этих точках не существует. Чтобы определить, действительно ли в точке, "подозреваемой" на экстремум, имеет место максимум или минимум функции, необходимо каждый раз проводить дополнительное исследование одним из перечисленных ниже способов.
Рис.2.1
Сравнение значений функций. Со значением функции в точке х 0, подозреваемой на экстремум, cравниваются значения функции в точках, лежащих справа и слева (но достаточно близко) от нее, т.е. в точках x 0+e и x 0-e, где e – малая положительная величина (рис.2.2). Очевидно, что если оба значения R (x 0+e) и R (x 0-e) меньше, чем R (x 0), то в точке x 0 – максимум функции, если R (x 0+e) > R (x 0) и R (x 0-e) > R (x 0), то в точке x 0 – минимум, а если R (x 0+e) > R (x 0) > R (x 0-e) или R (x 0+e) < R (x 0) < R (x 0-e), то в точке x 0 нет ни максимума, ни минимума функции.
Рис.2.2
Сравнение знаков производных. При этом способе исследования определяется знак производной в точках x 0+e и x 0-e. Если знаки различны, то в точке x 0 – экстремум функции (см. рис.2.2). При изменении знака плюс на минус в точке x 0 – максимум функции, при изменении знака минус на плюс – минимум. Если знаки одинаковые, то в рассматриваемой точке ни максимума, ни минимума функции нет.
Исследование знаков высших производных. Этот способ применим, если в точке x 0 существуют производные высших порядков, т.е. если функция R (х) непрерывна сама и имеет непрерывные производные 
и т.д.
В точке x 0, подозреваемой на экстремум, для которой 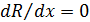вычисляется 
. Если 
, то в точке x 0 – максимум функции, а если 
, то минимум. Отрицательность означает, что в точке x 0первая производная меняет знак плюс на минус, и наоборот.
Если вторая производная в рассматриваемой точке равна нулю: 
, необходимо вычислить следующую производную. Если окажется, что 
, то вычисляют 
и т.д.
При этом руководствуются следующим правилом: если порядок первой производной, не обращающейся в нуль, нечетный 
, то в этой точке функция не имеет экстремума; если порядок первой производной, не обращающейся в нуль, четный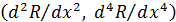 
, то в данной точке есть экстремум функции, который будет максимумом или минимумом в зависимости от того, отрицательна или положительна эта производная.
При решении практических задач оптимизации обычно требуется отыскать не какой-нибудь экстремум функции R (х), а наибольшее или наименьшее значение этой функции (рис.2.3). Точка наибольшего или наименьшего значения функции R (х) называют глобальными экстремумами в отличие от остальных, которые в это случае называются локальными. Так как по аналитической записи функции в общем случае невозможно определить число экстремумов, то для решения оптимизационной задачи необходимо: во-первых, найти все точки функции R (х), в которых может быть экстремум, во-вторых, исследовать все эти точки на экстремум и, в-третьих, среди локальных экстремумов нужного типа (максимум или минимум) найти глобальный. При большом числе локальных экстремумов требуется очень большой объем вычислений, который может быть сокращен за счет применения следующего правила: в непрерывных функциях одной переменной максимумы и минимумы чередуются, между двумя соседними максимумами расположен один минимум и, наоборот, между двумя минимумами – один максимум.
Рис.2.3
В практических задачах диапазон изменения независимой переменной x ограничен заданным интервалом (рис.2.4). Приведенную методику поиска экстремальных точек можно использовать лишь для внутренних точек интервала, поэтому в число подозрительных точек должны быть включены и крайние точки интервала, в которых может быть глобальный экстремум функции.
Рис.2.4
Наряду с аналитическими широкое распространение получили численные методы поиска экстремума функции, применение которых целесообразно в тех случаях, когда выражение целевой функции слишком громоздко и затрудняет получение аналитических зависимостей для производных, или когда целевая функция записана в неявном виде, что также осложняет вычисление производных.
Следует отметить, что численные методы поиска экстремум функции одной переменной имеют не только самостоятельное значение при решении оптимизационных задач, но и используются как вспомогательные методы при оптимизации функции нескольких переменных.
Метод локализации экстремума функции. Задача состоит в на хождении положения экстремума функции в интервале изменения переменной от x 0= а до х n= b. Для решения весь интервал изменения аргумента делится на N равных частей. На рис.2.5 показано такое деление для N = 4. При значениях переменных соответствующих границам участков (включая начальное и конечное значения), вычисляются значения функции R (х). Среди полученных значений R (х i), где i = 0, 1, 2, 3, … n, находится значение, соответствующее типу отыскиваемого экстремума. Так, если ищется минимум функции то наименьшее значение функции будет при x 2.
Рис. 2.5
После этого выбирается новый интервал, включающий два участка предыдущего интервала, непосредственно примыкающих к значению переменной x 2, соответствующему минимальному значении функции. Поскольку на границах выбранного нового интервала значения функции R (х) больше, чем в его середине, можно предположить, что минимум лежит в интервале x 1– x 3.
Таким образом, в результате проделанного анализа минимум функции локализован в интервале изменения переменной, вдвое меньшем начального. Применяя к нему описанную процедуру, т.е. разделяя его на четыре части, вычисляя значения функции на границах участков и выбирая значение переменной, обеспечивающее наименьшее значение функции, можно еще в два раза уменьшить рассматриваемый интервал изменения переменной. Повторяя эти действия многократно, можно добиться требуемой точности определения экстремума функции. Выбор значения N =4 оказывается наиболее целесообразным, так как в этом случае при переходе к новому интервалу, вдвое сужающему границы изменения независимой переменной, необходимо вычислить значения функции R (х) только в двух точках.
Абсолютная ошибка в определении положения экстремума оценивается по выражению
,
где 
– число расчетов целевой функции, которое при использовании этого метода является нечетным.
Относительная ошибка при числе расчетов целевой функции для 
составит
Метод "золотого сечения". Более высокую точность определения положения экстремума можно обеспечить, если разделять интервал, в котором ищется экстремальное значение функции, в некотором иррациональном соотношении.
Представим себе, что известны значения функции R (х) на границах интервала при x 0= а и х 3= b, а также еще в двух точках при x 1и x 2(рис.2.6). Тогда можно выбрать один из подынтервалов x 0 – x 2или x 1 – x 3, в котором отыскивается интересующее значение функции.
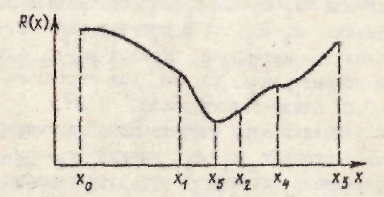
Рис.2.6
Допустим, что ищется минимум функции. Тогда есть основания полагать, что этот минимум локализован на участке. Необходимо выбрать в этом подынтервале x 1 – x 3точку х 4так, чтобы точки х 2и х 4делили интервал x 1 – x 3в таком же соотношении, в каком точки х 1, х 2 делят исходный интервал x 0 – x 3. Очевидно, что это предъявляет определенное требование и к выбору местонахождения точек х 1и х 2 в пределах исходного интервала x 0 – x 3.
Допустим, что длины подынтервалов x 0 – x 2 и x 1 – x 3равны, тогда отрезки x 0 – x 1 и x 2 – x 3также равны. При этих условиях для подынтервала x 1 – x 3должны быть равны отрезки x 1 – x 2 и x 4 – x 3.
Если воспользоваться обозначениями у = b -а= x 0- x 3, y 1= x 0- x 1= x 2 – x 3,
y 2= x 1- x 2= x 4- x 3,то для подобного деления; отрезков необходимо соблюдение условия
.
Преобразуя последнее равенство, нетрудно получить выражение
,
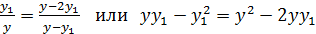которое приводится к квадратному уравнению
.
Решение этого уравнения позволяет найти требуемое отношение
.
Найденное отношение получило название "золотого сечения". Особенность его заключается в том, что если в исходном интервале отрезки x 0 – x 1 и x 2 – x 3 составляли по ~0,38 длины исходного отрезка x 0 – x 3, то в подынтервале x 1 – x 3, составляющем ~0,62 исходного интервала, отрезок x 1 – x 2 будет составлять ~0,38 длины подынтервала, так же, как и отрезок x 4 – x 3, а отрезок x 2 – x 3 ~0,62 длины подынтервала.
Если теперь выбрать новый подынтервал x 1 – x 4, то откладывая отрезок x 1 – x 5 равный x 2 – x 4, можно определить местонахождение точки х 5, при этом отрезок x 1 – x 5 будет составлять ~0,38 длины этого подынтервала.
Таким образом, одно вычисление функции позволяет локализовать экстремум в пределах ~0,62 длины исходного интервала.
Относительная погрешность нахождения экстремума будет определяться выражением
При том же числе вычислений функции s = 21 относительная погрешность составит
Иными словами, метод "золотого сечения" позволяет на порядок повысить точность нахождения экстремума по сравнению с методом локализации экстремума при одинаковом количестве вычислений значений функции.
Метод поиска экстремума с использованием чисел Фибоначчи. Числами Фибоначчи называют последовательность чисел, полученных из натурального ряда чисел на основании следующих рекуррентных соотношений: 
; F 1 = 1; F 0 = 1. Ниже приведены значения чисел Фибоначчи, полученные на основании указанных соотношений:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | ||
|
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|
| 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 | 6765 | 10949 | 17711 |
Последовательность поиска экстремума с помощью чисел Фибоначчи может быть такой:
1)определяется некоторое вспомогательное число N, зависящее от требуемой точности поиска экстремума 
: 
;
2)находится число Фибоначчи, определяемое соотношением
3)определяется минимальный шаг поиска экстремума
4) рассчитывается значение функции R (x) в начале интервала при x 0= а, т.е. R (a);
5) определяется следующее значение аргумента x 1= x 0+ D min Fs -2 и вычисляется значение функции R (x 1);
6) если был сделан удачный шаг, т.е. R (x 1) < R (x 0), то определяется следующее значение аргумента x 2= x 1+ D min Fs -3 и вычисляется значение функции R (x 2);
7) при неудачном шаге, R (x 1) > R (x 0), значение аргумента определяется выражением x 2= x 1- D min Fs -3.
Указанные действия повторяются до тех пор, пока не будут использованы все числа Фибоначчи в убывающей последовательности 
(рис.2.7).
При числе расчетов 21 относительная погрешность при использовании чисел Фибоначчи равна
,
что несколько ниже, чем при использовании метода "золотого сечения".
Рис.2.7
2.1.2. Методы нахождения экстремума функции нескольких переменных
Решение задачи оптимизации существенно усложняется, если критерий оптимальности является функцией нескольких независимых переменных. Особые трудности возникают при отсутствии непрерывности у всех или нескольких производных оптимизируемое функции.
Ниже рассматриваются необходимые и достаточные условия существования экстремума для непрерывных функций, имеющих непрерывные производные первого и второго порядка.
Для непрерывной функции многих переменных
, (2.3)
имеющей непрерывные производные первого и второго порядков по всем переменным х i (i = 1, 2,..., n), необходимым условием существования экстремума в точке 
(i = 1, 2,..., n) служит равенство нулю в этой точке частных производных по всем переменным. Точки, в которых возможен экстремум функции (2.3), определяются решением системы уравнений
(2.4)
Для того чтобы выяснить, действительно ли точка 
(i = 1, 2,..., n), координаты которой удовлетворяют условиям (2.4), является точкой экстремума функции (2.3), проверки экстремальности по всем переменным в отдельности оказывается недостаточно. В этом случае может быть использована следующая методика.
Предположим, что исследуется на экстремум точка с координатами
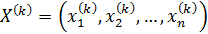, (2.5)
удовлетворяющими системе уравнений (2.4). Разложив функцию R (Х) = R (х 1, х 2,…, x n) в окрестности точки (2.5) в ряд Тейлора по приращению переменных 
, i = 1, 2,..., n, получим
(2.6)
В выражении (2.6) использована сокращенная форма представления членов разложения с производными выше первого порядка. Например, для функции двух переменных член 
раскрывается так:
Аналогично раскрываются и члены более высокого порядка при большем числе независимых переменных.
Опуская в разложении (2.6) члены, имеющие порядок малости по 
выше второго, и принимая во внимание, что члены первого порядка малости по обращаются в нуль, поскольку координаты точки 
удовлетворяют уравнениям системы (2.4), получим приближенное равенство
(2.7)
Из выражения (2.7) следует, что знак приращения функции d R в достаточно малой окрестности точки 
определяется производными второго порядка от R (Х) по всем переменным, включая и смешанные производные. Точка будет являться точкой экстремума функции R (Х), если при любых малых приращениях независимых переменных 
правая часть выражения (2.7) остается положительной для точки минимума и отрицательной для точки максимума функции.
2.1.3. Метод неопределенных множителей Лагранжа
Изложенный выше метод классического анализа функций может быть использован для нахождения экстремума функции при условии, что оптимизирующие переменные не связаны между собой какими-либо соотношениями, т.е. являются полностью независимыми. Такой экстремум называется безусловным. Однако при решении практических задач, связанных с оптимизацией какого-либо объекта, например, холодильной установки, часто приходится сталкиваться со случаями, когда оптимизирующие переменные связаны между собой соотношениями, имеющими вид равенства. В этом случае речь может идти только о нахождении условного экстремума оптимизируемой функции [16, 36].
Рассмотрим более подробно методику нахождения условного экстремума на примере функции двух переменных, хотя все изложенное ниже будет справедливо при любом числе оптимизирующих переменных. Представим, что необходимо определить экстремум функции
(2.8)
при условии, что переменные x 1, и х 2 связаны между собой соотношением
(2.9)
Это означает, что рассматриваются и сравниваются значения функции только для тех точек (в плоскости аргументов), которые лежат на линии, удовлетворяющей уравнению (2.9). На рис.2.8 изображены линии уровня рассматриваемой функции R (х 1, x 2) а, также нанесена зависимость (2.9).
Рис.2.8
Безусловный максимум рассматриваемой функции достигается в точке 0, в то время как условный экстремум имеет место в точке а. По образному выражению, приводимому А.Д. Мышкисом, безусловный максимум подобен вершине горы, а условный подобен высшей точке горной тропы, проекция которой на плоскость х 1 – x 2 выражена уравнением (2.9).
Если из уравнения связи (2.9) можно получить зависимость x 2 от х 1 в явном виде, т.е. выразить x 2 через х 1 (x 2 = f (х 1)), то функцию (2.8) можно записать в виде
В этом случае R становится функцией одной переменной. Условие связи (2.9) больше не действует, так как оно учтено подстановкой x 2 = f (х 1) и задача об отыскании экстремума функции R сводится к нахождению безусловного экстремума.
Аналогичный результат может быть получен, если уравнение (2.9) можно разрешить относительно х 2 или если это уравнение может быть представлено в параметрическом виде.
В общем случае для нахождения условного экстремума исходная функция (2.8) и уравнение связи (2.9) объединяются некоторой новой функцией – уравнением Лагранжа (лагранжианом)
,
которая представляет собой сумму исходной функции (2.8) и произведения уравнения связи (2.9), записанного в неявном виде, на некоторую неизвестную вначале величину 
, называемую множителем Лагранжа.
Применение метода неопределенных множителей Лагранжа позволяет заменить задачу отыскания условного экстремума функции (2.8) с учетом связи между переменными (2.9) задачей отыскания безусловного экстремума для лагранжиана L в соответствии с правилами, изложенными в п.2.1.2. Тогда уравнения (2.4) должны быть записаны в виде системы
что вместе с уравнением связи (2.9) образует систему из трех уравнений, позволяющую определить три искомые величины х 1, x 2 и l т.е. найти возможные точки условного экстремума. Полученные условия являются только необходимыми, методы определения достаточных признаков были рассмотрены выше.
Заметим, что ч исло уравнений связи должно быть меньше числа переменных.
Влияние связи между переменными на результаты оптимизации может быть проиллюстрировано следующим примером.
Пусть требуется определить такие размеры ресивера холодильной установки, при которых его суммарная поверхность и, в первом приближении, расход металла на его изготовление будут минимальны.
Для простоты представим ресивер в виде цилиндрического сосуда с плоскими днищами (рис.2.9).
Рис.2.9
Поверхность такого аппарата будет определяться выражением
(а)
Для нахождения экстремума этой функции в соответствии с (2.4) должны быть взяты производные по переменным и приравнены нулю:
, (б)
. (в)
Из выражения (в) следует, что так как 
, то R min =0. Подставив это значение в (б), получим 
; а так как , то H min = 0. Подставляя полученные значения R min =0 и H min = 0 в уравнение (а), находим S min = 0.
Таким образом, минимальная поверхность соответствует случаю, когда такой аппарат не будет существовать.
Такой ответ соответствует безусловному экстремуму и получен в связи с некорректной постановкой задачи.
Правильная постановка задачи требует следующей формулировки: определить такие размеры ресивера холодильной установки с заданной вместимостью (внутренним объемом V), при которых его суммарная поверхность будет минимальна.
Внутренний объем аппарата равен
(г)
Выражение (г) устанавливает связь между переменными, следовательно, они не являются полностью независимыми, и в рассматриваемом случае речь может идти только о нахождении условного экстремума, удовлетворяющего как уравнению (а), так и уравнению связи (г).
Для решения должно быть записано уравнение Лагранжа
, (д)
взяты от него производные по R и Н и приравнены нулю:
(е)
. (ж)
Из выражения (ж) следует, что 
, откуда
(з)
Подставляя выражение (з) в уравнение (е), получаем 
, откуда
(и)
Подставляя выражения (з) и (и) в уравнение связи (г), можно вычислить множитель Лагранжа
(к)
Используя полученное выражение (к) для l, находим окончательные выражения для R опт и H опт:
,
а по ним и минимальное значение поверхности аппарата
.
Нетрудно убедиться, что полученное в этом случае решение существенно отличается от найденного ранее безусловного минимума. Следует заметить, что приведенная задача могла быть решена и путем выражения одной переменной через другую из уравнения связи (г), а затем подстановкой полученной зависимости в исходное уравнение (а), что предлагается сделать читателям.
2.1.4. Линейное программирование
При решении ряда технических задач выражение для критерия оптимальности может быть представлено в виде линейной функции от входящих в него оптимизирующих переменных. При этом на оптимизирующие переменные могут быть наложены некоторые ограничивающие условия также в форме линейных равенств или неравенств. В этом случае решение оптимизационных задач осуществляется методами линейного программирования.
Выражение для целевой функции в общем виде может быть представлено выражением
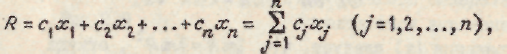(2.10)
где 
– заданные постоянные коэффициенты.
Выражение (2.10) называется линейной формой. На выбор оптимальных значений переменных накладываются дополнительные условия, устанавливающие связь между оптимизирующими переменным (они могут включать в себя как равенства, так и неравенства):
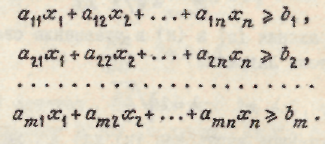(2.11)
Коэффициенты 
в (2.10) и 
в выражениях (2.11) являются действительными числами и могут быть положительными и отрицательными, среди них могут быть и равные нулю. Число ограничений типа равенств не должно превышать общего числа оптимизирующих переменных в линейной форме. Число неравенств может быть произвольным.
В задачах линейного программирования обычно предполагают, что оптимизирующие переменные неотрицательны, т.е. 
, j = 1, 2,..., п. Также считают, что все величины 
в выражениях (2.11) отличны от нуля и положительны. Если какое-либо значение bi окажется отрицательным, то, умножая правую и левую части соответствующего выражения на -1, его приводят к виду, когда правая часть принимает положительное значение. Если какая-либо величина 
оказывается равной нулю, то в левую и правую части соответствующего выражения (2.11) добавляется слагаемое x n+1, что делает величину 
отличной от нуля. При этом считают, что добавленное слагаемое вошло и в линейную форму (2.10), но с нулевым коэффициентом (с n+1 = 0), что не изменило выражения для целевой функции.
Для сокращения записи условия (2.11) могут быть представлены в виде
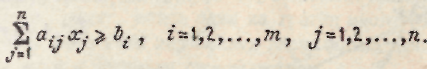(2.11, а)
Оптимальным решением задачи линейного программирования является такая совокупность значений независимых переменных, которая удовлетворяет условиям (2.11) и обеспечивает, в зависимости от постановки задачи, максимальное или минимальное значение линейной формы.
Обычно считают, что оптимум достигается при максимальном значении линейной формы. Случай, когда требуется найти минимальное значение линейной формы, может быть сведен к задаче максимизации путем изменения знаков у всех коэффициентов 
(j = 1,2,...., n), т.е.
Пусть нужно решить задачу максимизации критерия оптимальности, имеющего вид
(а)
т.е. рассматривается выражение, в котором п = 2, с 1 = 1, с 2 = 1, при налички ограничений на оптимизирующие переменные x 1 и х 2 типа равенств
(б)
и неравенств
. (в)
В выражениях (б) согласно (2.11) а 11 = 2, а 12 = 1, а 21= 1, а 22= 2, b 1 = 1, b 2 =1.
Так как размерность рассматриваемой задачи равна двум, процесс решения может быть представлен графически. Равенства (б) на фазовой плоскости переменных x 1 и x 2, (рис.2.10) определяют область возможных значений этих переменных, которая расположена в первом квадранте и ограничена линиями, соответствующими уравнениям
.
На рис. 2.10 линии, ограничивающие рассматриваемую область X, заштрихованы с внешней стороны.
Рис.2.10
В соответствии со структурой линейной формы (2.10) и (а) производные от критерия оптимальности по оптимизирующим переменным постоянны, непрерывны и нигде в области X не обращаются в ноль: 
; 
. Это означает, что экстремум целевой функции может быть достигнут только на границе области X. Величина критерия оптимальности имеет постоянное значение вдоль линии l, определяемой уравнением
(г)
На рис.2.10 эта линия изображена для значения l = 0,4. Если ее перемещать на плоскости (x 1, x 2) параллельно самой себе в направлении, указанном стрелкой, то значение l, а следовательно, и величина целевой функции будут возрастать.
Очевидно, что максимальному значению R в рассматриваемом случае соответствует предельное положение линии l в области X, когда она проходит через точку К, являющуюся вершиной многоугольника, ограниченного линиями (б) и (в). Максимальное значение целевой функции определяется координатами точки К, которые могут быть определены совместным решением уравнений (б):
(д)
Подстановка полученных значений оптимизирующих переменных (д) в уравнение линейной формы (а) позволяет определить максимальное значение целевой функции 
В рассмотренном примере максимальное значение целевой функции обеспечивается при некоторых конечных значениях оптимизирующих переменных. Однако в задачах линейного программирования возможны случаи, когда решению задачи соответствует бесконечный набор значений оптимизирующих переменных. Геометрически это соответствует варианту, когда одна из границ многоугольника области возможных изменений переменных параллельна линии l, определяемой выражением критерия оптимальности.
Если для условий предыдущего примера при ограничениях 2 x 1 + x 2= 1, x 1 + 2 x 2= 1, х 1>= 0, х 2 >= 0целевая функция будет иметь вид R = 2 x 1 + x 2, то максимум функции будет иметь место по линии АК (см.рис.2.10). В этом случае уравнение для линии l 1имеет вид l 1= 2 x 1 + x 2 = 0,4. Поскольку ограничения типа равенств остались неизменными, значения 
и 
также не изменились, а максимальное значение целевой функции будет R max= 1, причем это значение целевой функции может быть достигнуто при различных сочетаниях x 1 и х 2, удовлетворяющих отрезку АК.
В рассмотренном примере система ограничений описывает замкнутую область возможных значений оптимизирующих переменных. Иногда система ограничений может определить и незамкнутую область. Так, если ограничения описываются выражениями 
=1, 
, x 1>= 0, x 2>= 0 (рис.2.11), то целевая функция вида R =х 1+ х 2достигнет максимума при бесконечно боль–значениях х 1, и х 2, так как возможности перемещения линии 
(l = 0,25) в направлении увеличения R не ограничены.
В то же время, при незамкнутой области изменения переменных максимум целевой функции может лежать и не в бесконечности. Если при перечисленных выше ограничениях целевая функция имеет вид R = 3 х 1- х 2, то перемещенке линии l 1 = 3 х 1- х 2 = 0,5 ограничено. Решая систему уравнений
8 x 1-4 x 2=1, 8 x 1-2 x 2=2,
можно вычислить значения 
, 
и определить максимальное значение целевой функции R max 
.
Рис. 2.11
В общем случае произвольного числа п оптимизирующих переменных геометрическая интерпретация задачи невозможна. Область допустимых значений переменных в п –мерном пространстве является многогранником, ограниченным гиперплоскостями, уравнения которых задаются ограничениями (2.10). Поверхность, вдоль которой критерий оптимальности имеет постоянное значение, будет представлять собой также гиперплоскость определяемую конкретным видом выражений (2.10).
2.1.5. Нелинейное программирование
Как уже отмечалось, математическая формулировка задачи оптимизации сводится к отысканию наибольшего или наименьшего значения функции нескольких переменных
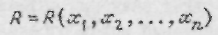(2.12)
при наличии ограничений на оптимизирующие переменные, записанных в виде равенств или неравенств
. (2.13)
В тех случаях, когда аналитический вид соотношений (2.12) и (2.13) известен, для нахождения экстремума могут быть использованы описанные выше методы.
Однако при решении большого числа практических задач приходится сталкиваться со случаем, когда выражение (2.12) целевой функции не может быть записано в явном виде при заданной совокупности значений оптимизирующих переменных xj. Наличие ограничений (2.13), которые могут быть выражены трудно вычислимыми функциями, еще более затрудняет нахождение оптимального решения. Решение такого рода задач с нелинейными и трудно вычислимыми соотношениями, определяющими критерий оптимальности и ограничения на переменные, осуществляется методами нелинейного программирования. Как правило, задачи нелинейного программирования решаются только численными методами, что возможно практически только при использовании ЭВМ.
Методы нелинейного программирования представляют собой методы последовательного улучшения начального решения, или многошаговые методы. При этом в задачах нелинейного программирования обычно заранее нельзя сказать, какое число шагов гарантирует нахождение оптимума с заданной степенью точности. Разработано большое количество разнообразных методов нелинейного программирования, которые по способу определения шага поиска подразделяются на безградиентные и градиентные методы поиска оптимума.
При решении конкретных задач оптимизирующие переменные могут иметь различный физический смысл (например, температура, давление, расход какой-либо среды и т.п.) и соответственно различные единицы измерения. При использовании численных методов решения оказывается целесообразным приведение переменных к безразмерному нормализованному виду.
Для нормализации их на основе физических представлений устанавливаются возможные диапазоны изменения переменных. Допустим, что некоторая физическая величина vj может менять свое значение в пределах vj max > vj > vj min. Тогда в безразмерной нормализованной форме эта переменная может быть представлена таким образом:
, (2.14)
при этом предел изменения новой нормализованной переменной будет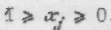 
.
Безградиентные методы поиска оптимума. Безградиентными методами поиска экстремума целевой функции называются такие, в которых в процессе поиска используется сравнительная оценка величины критерия оптимальности в результате выполнения очередного шага.
Метод сканирования. Этот метод заключается в последовательном вычислении значения целевой функции ряде точек, принадлежащих области изменения оптимизирующих переменных, и нахождении среди этих точек такой, в которой целевая функция достигает своего экстремального значения. Точность метода сканирования зависит от того, насколько часто располагаются выбранные точки в области изменения оптимизирующих переменных.
Достоинствами метода сканирования является то, что его применение гарантирует отыскание глобального экстремума, а так же независимость поиска от вида оптимизируемой функции. Недостатком является необходимость вычисления значений целевой функции для большого числа точек.
Дополнительные ограничения на независимые переменные не усложняют, а наоборот, упрощают применение метода сканирования, так как точки, не удовлетворяющие заданным условиям, просто исключаются из рассмотрения и целевая функция для них не рассчитывается.
Количество расчетов, которые должны быть произведены для нахождения экстремума, определяются из следующих соображений.
Если задана точность определения экстремума D, т.е. если найденные значения нормализованных переменных не должны отличаться от истинного положения оптимума больше, чем на величину D, то общее число рассчитываемых значений целевой функции составит
,
где п – число оптимизирующих переменных (размерность) решаемой задачи.
Так, для отыскания оптимума функции двух переменных R (х 1, x 2) с точностью 
потребуется выполнить 
, а для функции трех переменных 
расчетов.
Степенная зависимость числа расчетов от размерности задачи ограничивает эффективное использование метода сканирования либо задачами невысокой размерности, либо невысокой точностью поиска экстремума.
Для уменьшения числа расчетов существуют алгоритмы с переменным шагом сканирования, когда вначале выполняется грубый поиск, позволяющий выявить область нахождения глобального экстремума, а затем, в пределах этой области, осуществляется поиск с меньшим шагом.
Метод поочередного изменения переменных. Этот метод, известный также как метод Гаусса – Зейделя, сводится к изменению в произвольной последовательности значения оптимизирующих переменных. Изменение каждой переменной производится до тех пор, пока не будет достигнуто экстремальное значение (максимум или минимум) критерия оптимальности. После того как достигнут оптимум по данной переменной, начинается варьирование следующей.
Недостатком этого метода является трудность поиска при наличии ограничений на значения оптимизирующих переменных или при наличии "оврагов" у оптимизируемой функции (оврагом называется особенность целевой функции, заключающаяся в том, что от определенных оптимизирующих переменных функция зависит очень слабо).
Симплексный метод. Все безградиентные методы поиска оптимума связаны с выполнением большого числа расчетов. Для сокращения числа расчетов и определения направления поиска оптимума был разработан симплексный метод. Идея этого метода заключается в том, что по известным значениям целевой функции в вершинах выпуклого многогранника, называемого симплексом, находится направление, в котором надо сделать следующий шаг, чтобы получить наибольшее изменение (увеличение или уменьшение) критерия оптимальности.
Понятие симплекс в n –мерном пространстве характеризует выпуклый многогранник, имеющий п+1 вершину, каждая из которых образуется пересечением п гиперплоскостей данного пространства.
Примером симплекса в двухмерном пространстве (п =2) является треугольник, а в трехмерном пространстве (п =3) – любая четырехгранная пирамида, имеющая четыре вершины.
Симплекс обладает одним свойством, которое и дало возможность использовать его для проведения оптимизационных расчетов: против любой его вершины С j – расположена только одна грань, на которой можно построить новый симплекс, отличающийся от прежнего расположением новой вершины С j *, в то время как все остальные вершины будут совпадать. При этом новая вершина С j *может находиться по другую сторону грани от вершины С j.
Поиск оптимума (минимума) функции двух переменных симплексным методом показан на рис.2.12.
Рис.2.12
Производится расчет значений целевой функции в точках 
, соответствующих начальному положению симплекса (треугольника). Из найденных трех значений целевой функции выбирается наибольшее. В рассматриваемом случае наибольшим значением будет с 10. После этого строится новый симплекс с 11, с 20, с 30: из вершины с 10 на противоположную сторону опускается перпендикуляр и на продолжении прямой с 10– А откладывается отрезок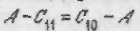 
. Штриховая линия со стрелкой показывает преобразование симплекса. В новой вершине с 11 вычисляется значение целевой функции и сравнивается со значениями для других вершин с 20 и с 30. Затем находится вершина, соответствующая наибольшему значению целевой функции (с 30) и строится следующие симплекс с 11, с 20, с 31, и т.д.
В результате исключения вершин симплексов с максимальным значением целевой функции процесс направлен к искомой точке с ее минимальным значением. На рис. 2.12 показано, что вблизи точки экстремума может произойти зацикливание счета, вызванное тем, что вершины с 13 и с 14 будут иметь максимальное значение целевой функции в симплексах с 13, с 23, с 33 и с 14, с 23, с 33. Тогда от симплекса с 13, с 23, с 33 будет осуществляться переход к симплексу с 14, с 23, с 33, а от последнего – опять к симплексу с 13, с 23, с 33. Для устранения зацикливания необходимо уменьшить шаг спуска в районе оптимума. Для этого на продолжении прямой с 13– В должен быть отложен не отрезок В – с 14= с 13– В, а отрезок В – с 14*=0,5(с 13– В). В результате в симплексе с 14*, с 23, с 33 наибольшее значение целевой функции будет уже в вершине с 33. Критерием окончания поиска служат размеры симплекса. Поиск оптимума прекращается, если все ребра симплекса станут меньше наперед заданной, достаточно малой величины.
В качестве начального симплекса лучше всего использовать правильный симплекс со всеми вершинами и гранями, одинаково удаленными от центра (в рассмотренной двухмерной задаче – равносторонний треугольник).
Градиентные методы поиска оптимума. В основу градиентных методов положены вычисление и анализ производных целевой функции.
Когда аналитический вид целевой функции (2.12) известен, вычисление производных <
