Моделирование фрактальных шумов
Выше отмечалось, что временные ряды, представляющие самоподобные фрактальные шумы, также обладают свойством долгой памяти, поэтому вначале рассмотрим ситуацию с моделированием фрактальных шумов.
В общем случае зависимость спектров мощности (квадраты амплитуд преобразования Фурье) от частоты характеризуется степенным законом вида 
. Среди шумов большой известностью пользуется белый шум со спектральным показателем β= 0. Иначе говоря, спектр белого шума не зависит от частоты. Подобно спектру белого света спектр белого шума является плоским только в некотором конечном диапазоне частот. Тем не менее, эти спектры позволяют моделировать бесчисленное множество процессов в широком диапазоне научных дисциплин.
Проинтегрировав белый шум один раз по времени, получаем коричневый шум (проекцию броуновского движения на одно пространственное измерение), который имеет спектр мощности, пропорциональный 
. Но белый и коричневый шумы далеко не исчерпывают все спектральные возможности: между ними располагается розовый шум со спектром 
, а за коричневым - черный, пропорциональный , где β > 2 [13].
И розовый, и коричневый шумы распространены весьма широко. Розовые процессы возникают во многих физических ситуациях (фликкер-шум) и находят эстетические применения в музыке и других видах искусства. Черные спектры описывают развитие во времени многих катастрофических событий: разливы рек, различные аварийные ситуации, обвал рынка и др.
В качестве примера самоподобных процессов приведем результаты моделирования коричневого и розового шумов. Генерирование коричневого шума сводится к суммированию независимых случайных чисел и реализуется сравнительно легко посредством табличного расчета в Excel. На рис.3.26 приведена реализация процесса, определяющего коричневый шум, длиной 1000 точек.
Рис. 3.26. Реализация процесса коричневого шума
На рис.3.27 приведены рассчитанные значения АКФ и СП, откуда по характеру изменений этих параметров следует вывод о том, что коричневый шум обладает свойством долгой памяти, поэтому может быть отнесен к процессам класса ARFIMA.
Рис. 3.27. АКФ (слева) и СП (справа)
Сравнительно простой метод генерирования розового шума состоит в том, чтобы сложить несколько релаксационных процессов со значениями времен релаксации τ, образующими самоподобную прогрессию с коэффициентом подобия 10 (или еще меньше - для лучшей сходимости) [13]. Укажем расчетную формулу, из которой с помощью генератора случайных чисел rn и рекуррентного соотношения
получаем требуемый ряд.
В расчетной формуле ρ - требуемый коэффициент корреляции между соседними случайными значениями. Со временем релаксации τ этот коэффициент связан соотношением 
. Таким образом, для набора значений времени релаксации, каждое из которых в 10 раз превосходит предыдущее (τ =1, 10, 100,…), коэффициенты корреляции получаются вычислением последовательных корней десятой степени (т.е. ρ= 0,37; 0,90; 0,99, …). Результаты расчета этого ряда протяженностью 1000 точек приведены на рис.3.28.
Рис. 3.28. Реализация процесса розового шума
На рис.3.29 приведены рассчитанные значения АКФ и СП, откуда по характеру изменений этих параметров следует вывод о том, розовый шум, также как и коричневый, является рядом с долгой памятью.
Рис. 3.29. АКФ (слева) и СП (справа)
Имитация процесса ARFIMA
Существуют различные способы имитации временных рядов, которые описываются моделью ARFIMA. Наиболее просто такой процесс может быть получен из процесса ξ i, подчиняющегося нормальному распределению с нулевым средним и среднеквадратичным отклонением (СКО) σ:
(3.43)
где 
k ≥ 1. (3.44)
По существу, выражение (3.43) определяет собой свертку гауссова процесса с бесконечным рядом. Ясно, что точность имитации процесса определяется числом членов ряда в формуле (3.43).
В качестве примера для d =0,2 приведем результаты имитации ряда по выражению (3.43), состоящего из 1000 точек, при выборе процесса ξ i, подчиняющего нормальному распределению с нулевым средним и СКО = 1, и при учете первых десяти коэффициентов ψ k, рассчитанных по выражению (3.44). При этом относительное расхождение между десятым и девятым коэффициентами ψ k составляет 7,5%. На рис.3.30 приведена разыгранная реализация такого ряда.
Рис.3.30. Смоделированная реализация ряда
Для оценки наличия в этом ряде ДП, т.е. значительной корреляционной связи на больших лагах, рассчитаем его АКФ, которая показана на рис.3.31.
Рис.3.31. АКФ смоделированного ряда
Как видно, изменение корреляционной связи разыгранного ряда характеризуется сравнительно долгой положительной связью, что является подтверждением наличия ДП ряда. Кроме того, можно сравнить коэффициенты корреляции, рассчитанные по формуле (3.40), с полученными при моделировании. В табл.3.6 приведены первые пять значений указанных коэффициентов.
Таблица 3.6 Рассчитанные и смоделированные значения коэффициентов корреляции
| Лаг | Значения АКФ (расчет) | Значения АКФ (модель) |
| 1 2 3 4 5 | 0,255 0,165 0,130 0,109 0,096 | 0,292 0,154 0,136 0,119 0,090 |
Как указывалось выше, кроме положительной корреляционной связи на больших лагах, другой характеристикой, определяющей наличие долгой памяти, является вид СП, которая для разыгранного ряда приведена на рис. 3.32. Как следует из графика спектра, мощность сигнала сосредоточена в основном в области низких частот, что также позволяет предположить наличие ДП в разыгранном ряде.
Рис.3.32. Спектральная плотность смоделированного ряда
Приведем еще один пример разыгранного ряда, отличающего от рассмотренного только изменением на порядок значения СКО процесса ξ i, которое в этом случае принято равным 0,1 вместо 1 в первом примере. На рис.3.33 – 3.35 приведены, соответственно, смоделированный ряд, графики АКФ и СП.
Рис.3.33. Смоделированная реализация ряда
Рис.3.34. АКФ смоделированного ряда
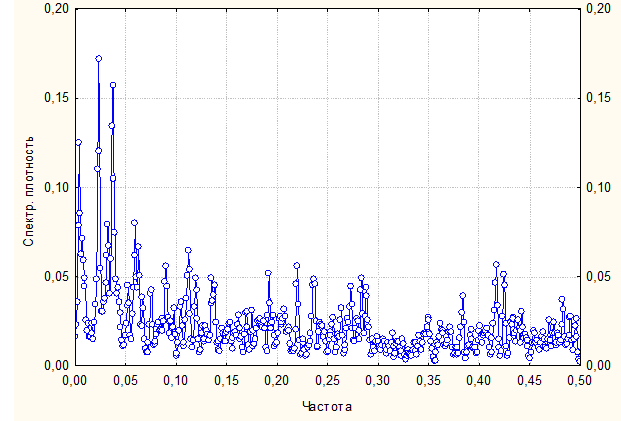
Рис.3.35. Спектральная плотность смоделированного ряда
Как видно, и в этом случае разыгранный ряд обладает свойством ДП.
