Долгая память временного ряда

Долгая память (ДП) или долговременная корреляция является свойством, описывающим корреляционную структуру временного ряда. При наличии ДП сильная зависимость между значениями ряда существует даже у значительно отстоящих друг от друга отсчетов.

Впервые процессы с ДП были предложены в работах Г.Херста в середине 50-х гг. прошлого века при изучении оптимальных размеров водохранилищ на реке Нил [8]. До работ Херста в гидрологии рассматривались модели, которые предполагали, что притоки и оттоки рек являются независимыми или слабо зависимыми во времени. При этом анализ истории изменения уровней воды в Ниле (благодаря записям египетских жрецов Херст располагал данными, охватывающими почти 800-летний период) не давал никакой полезной информации для предсказания будущего поведения реки. Иначе говоря, эффект крупного паводка должен был быстро исчезать, не оказывая влияния на анализируемый ВР. В этом случае речь идет о процессах с нулевой памятью (отсутствие корреляции) или о краткой памяти (корреляция только между близкими значениями ряда). К заслугам Херста можно отнести его вывод о том, что подобные модели недооценивают сложность гидрологических колебаний, а изучение предшествующих уровней воды в накопителях представляет ценную информацию относительно будущего поведения реки.

Существует несколько возможных определений процесса с ДП. Обычно ДП описывается в виде автоковариаций или спектральной плотности. Положим, что является временным рядом. Если ряд - стационарный, то математическое ожидание E (Х _t) = μ и автоковариационная функция γ(h)= Cov (X_t, X_t ₊ _h) не зависят от времени t. Общепринятое определение ДП временного ряда заключается в следующем: процесс обладает долгой памятью, если величина

(3.22)

не является конечной.

Альтернативная запись определения (3.22) сводится к следующей:

(3.23)

Кроме того, имеются еще иные дефиниции во временной области, в частности, ДП характеризуется гиперболическим спаданием автоковариаций

(3.24)

где d - так называемый параметр ДП; L ₁(h) - медленно изменяющаяся функция.

Примерами медленно изменяющихся функций являются:

L (h) = log x; L (h) = log(log x); L (h) = 1/log x.

Гиперболическое убывание автоковариаций для ряда с ДП противопоставляется экспоненциальному спаданию, характерному для процессов класса ARMA, которые можно охарактеризовать как процессы с короткой памятью.

ДП может быть определена и в частотной области. В случае если Х _t имеет непрерывную функцию распределения, его спектральная плотность (СП) выражается следующим образом

. (3.25)

Здесь S (f) - неотрицательная четная функция с периодом 2π. Принято считать, что ряд Х _t имеет долгую память, если

(3.26)

т.е. СП неограниченна на низких частотах.

Последнее выражение вблизи нулевой частоты может быть представлено в таком виде

(3.27)

где - медленно изменяющаяся функция.

В качестве примера на рис.3.21 приведен ВР изменения индекса РТС при общем объеме наблюдений, составляющем 3329 точек.

Рис.3.21. Временной ряд индекса РТС

Характер этого ряда не дает никаких оснований считать изменение индекса РТС процессом с ДП. Но его АКФ и СП, приведенные, соответственно, на рис.3.22 и 3.23, свидетельствуют о принадлежности анализируемого ряда к процессам с долговременной корреляцией. Как видно из приведенных рисунков, АКФ, которая рассчитана до лагов, составляющих 200 дней, спадает очень медленно: на границе диапазона при h = 200 величина АКФ составляет примерно 75% от максимального значения. В то же время СП сосредоточена вблизи нулевой частоты.

Рис.3.22. Автокорреляционная функция ряда индекса РТС

Рис.3.23. Спектральная плотность ряда индекса РТС

Поясним такое поведение спектра [10]. Подобный ряд можно рассматривать как процесс, обладающий трендом только в среднем, который имеет вид

Y_t = m (t) + X_t, (3.28)

где X_t - стационарный ряд.

Предположим, что член m (t), характеризующий тренд, или меняется гладко во времени, или имеет небольшое число далеко отстоящих друг от друга точек разрыва. Рассмотрим преобразование Фурье для функции m (t):

(3.29)

Вследствие того, что m (t) - действительная функция, получаем

В случае, если m (t) = A costω₀ + B sintω₀, то d μ_i(ω) = 0, ω ≠ ω₀, i = 1, 2. Таким образом, при порождении m (t) только одной частотой ω₀ величина d μ(ω) обращается в нуль всюду, кроме этой частоты.

Обычно полагают, что тренд m (t) есть монотонно возрастающая или, по крайней мере, непериодическая функция. Например, если m (t) является полиномом по t, т.е.

то тренд m (t) - непериодическая функция или, иначе говоря, ее «период» бесконечен. Это действительно так, потому что «период» периодической функции есть время, в течение которого функция не повторяет себя, а это время для полинома бесконечно.

Таким образом, непериодическая функция m (t) имеет бесконечный период, что соответствует нулевой частоте, и, следовательно, для такого тренда величина d μ(ω) в формуле (3.29) обращается в нуль для всех ω ≠ 0. Вследствие этого СП неслучайной непериодической функции всюду равна нулю и имеет скачок в начале координат. Амплитуда этого скачка пропорциональна дисперсии функции.

Показанная на рис.3.24 гистограмма наблюдений изменения индекса РТС обладает весьма интересными особенностями. В частности, для нее характерны несимметричность распределения, доминирующие малые значения индекса, принадлежность, скорее, к экспоненциальному распределению, чем к какому-либо другому.

Рис.3.24 - Гистограмма изменения индекса РТС

Описательные статистики для этих наблюдений представлены в табл.3.5.

Таблица 3.5 Описательные статистики индекса РТС

Cтатистика	Значение
Среднее	648,90
Стандартная ошибка	11,28
Медиана	360,88
Мода	83,56
Стандартное отклонение	651,11
Дисперсия выборки	423949,51
Эксцесс	0,28
Асимметричность	1,27
Интервал	2449,98
Минимум	38,53
Максимум	2487,98
Сумма	2160205,21
Счет	3329

Свойства модели ARFIMA

Долговременная зависимость ВР определяет его структурное поведение на больших временных интервалах, что характеризует устойчивое поведение ВР, т.е. значимую связь между очень удаленными наблюдениями.

Временной ряд X_t описывается моделью ARFIMA (p, d, q), если выполняется равенство (3.3)

(В)(1 – B) ^d X_t = θ(В) a_t.

Однако для этой модели показатель d может принимать дробные значения, следовательно, модель ARFIMA (p, d, q) расширяет класс параметрических моделей. Впервые процессы с ДП в таком виде были введены в работах [9,11], где проанализированы основные свойства таких временных рядов. Кроме того, временные ряды, представляющие самоподобные фрактальные шумы, также обладают свойством долгой памяти [13].

Вследствие того, что далее будет указана связь между показателем d и параметром Херста H, отметим здесь только основные свойства последнего. Параметр H назван показателем Херста в честь английского ученого-гидролога Г.Херста, много сделавшего при строительстве дамб и плотин на Ниле.

Имеются три граничных значения для показателя Херста:

· H = 0,5;

· 0 < H < 0,5;

· 0,5 < Н < 1,0.

При H = 0,5 события случайны и некоррелированны. Функция плотности вероятности может быть нормальной кривой, однако это не обязательное условие. Отличие параметра H от значения 0,5 означает, что наблюдения не являются независимыми. Каждое наблюдение несет память о всех предшествующих событиях. Это не кратковременная память, которую часто называют "марковской". Это долговременная память, которая теоретически может сохраняться навсегда. Недавние события имеют влияние большее, чем события отдаленные, но остаточное влияние этих последних всегда ощутимо. В долговременном масштабе система, которая дает статистику Херста, есть результат длинного потока взаимосвязанных событий. То, что случается сегодня, влияет на будущее.

Второй случай при 0 < H < 0,5 соответствует антиперсистентным или эргодическим рядам. Такой тип системы часто называют "возврат к среднему". Если система демонстрирует рост в предыдущий период, то, скорее всего, в следующем периоде начнется спад. И наоборот, если происходило снижение, то вероятен близкий подъем. Устойчивость такого антиперсистентного поведения зависит от того, насколько Н близко к нулю. Такой ряд более изменчив, чем случайный ряд, так как состоит из частых реверсов спад-подъем.

При 0,5 < Н < 1,0 получаем персистентные или трендо-устойчивые ряды. Если ряд возрастает (убывает) в предыдущий период, то, вероятно, он будет сохранять эту тенденцию какое-то время в будущем. Устойчивость трендов или сила персистентности увеличивается при приближении Н к единице (100% корреляции). Чем ближе Н к значению 0,5, тем более зашумлен ряд и тем менее выражен его тренд. Персистентные временные ряды представляют собой более интересный класс, так как оказалось, что они не только обнаруживаются в природе (это открытие принадлежит Херсту), но и свойственны рынкам капитала.

Установлено [11], что между параметрами d и Н существует следующая зависимость

d = H - 0,5. (3.30)

Введение дробного показателя d можно пояснить следующим образом. Известно, что броуновское движение определяется непрерывным стохастическим процессом с независимыми гауссовыми приращениями и спектральной плотностью, обратно пропорциональной квадрату частоты, т.е. f ^-2. Его производной является непрерывный процесс белого шума с постоянной спектральной плотностью. Фрактальное (дробное) броуновское движение (ФБД) есть обобщение этих процессов. Основные свойства ФБД сводятся к следующим:

1. ФБД с параметром H (обычно 0 < H < 1) является (0,5 – H)-ой дробной производной от броуновского движения.

2. Спектральная плотность ФБД пропорциональна f ^-2 ^H ^-1.

3. Ковариационная функция ФБД пропорциональна (k – временной лаг).

Броуновское движение возникает при суммировании независимых приращений [13]. Суммирование (или интегрирование) приращений преобразует спектр из f ⁰ в проинтегрированный процесс со спектром, пропорциональным f ^-2. Возникает вопрос: нельзя ли получить с помощью интегрирования и процессы со спектром, определяемым f ^-1? Положительный ответ на этот вопрос возможен в ситуации при введении дробного интегрирования. Поскольку интегрирование приводит к умножению спектральной плотности на f ^-2, определим полуцелое интегрирование как операцию, которая умножает СП на f ^-1. Отметим, что дробное интегрирование и дифференцирование уже довольно давно применяются в квантовой механике и других областях науки.

Дискретным аналогом броуновского движения является процесс случайного блуждания или ARIMA (0,1,0), определяемый выражением

(1 – B) X_t = a_t. (3.31)

Первая разность процесса { X_t } дает белый шум, т.е. X_t - X_t _- ₁ = a_t. По аналогии с определением непрерывного белого шума охарактеризуем дробно дифференцированный белый шум с параметром H как (0,5 – H)-ую разность дискретно-временного белого шума. По существу, взятие разности эквивалентно операции дифференцирования, поэтому можно использовать термин «дробное дифференцирование» вместо «дробной разности». Оператор дробного дифференцирования (1 – B) ^d определяется по биноминальной теореме для нецелых показателей в следующем виде

где .

После преобразований получаем такой результат

(1 – B) ^d = 1 – dB – (1/2) d (1 – d) B ² – (1/6) d (1 – d) (2 – d) B ³ - … (3.32)

В этих выражениях учтем, что дискретно-временным аналогом непрерывного шума с параметром H является процесс X_t = (1 – B)^- ^d a_t или (1 – B) ^d X_t = a_t.

Обозначим процесс { X_t } как ARFIMA (0, d,0) и будем считать его в качестве естественного расширения методологии Бокса-Дженкинса для нецелых d.

Рассмотрим свойства процесса ARFIMA (0, d,0), который можно записать в виде

(1 – B) ^d X_t = a_t, (3.33)

где a_t - определяет процесс белого шума, состоящий из независимых идентично распределенных случайных величин, с нулевым средним значением и дисперсией .

Пусть { X_t } является процессом ARFIMA (0, d,0). В работе [11] приведены основные свойства этого процесса.

1. При d < 0,5 процесс { X_t } является стационарным и имеет представление в виде бесконечного ряда скользящего среднего

(3.34)

где

При k → ∞ получаем

2. При d > - 0,5 процесс { X_t } является обратимым и имеет представление в виде бесконечного авторегрессионного ряда

(3.35)

где

При k → ∞ получаем

Далее, в пп.3, 4 допустим, что -0,5 < d < 0,5.

3. Спектральная плотность процесса { X_t } определяется в виде

S (ω) = (2sin 0,5 ω)^{-2 d} для 0 < ω ≤ π,

S (ω) ~ ω^-2 ^d для ω → 0.

4. Автоковариационная функция процесса { X_t } имеет вид

Автокорреляционная функция определяется как

В частности, γ₀ = (-2 d)! / [(- d)!]² и ρ₁ = d / (1 – d).

При k → ∞ получаем (3.36)

Рассматриваемый процесс ARFIMA (0, d,0) может быть подвергнут интегрированию или дифференцированию конечное целое число раз до тех пор, пока d находится в интервале [-1/2, 1/2], и будет являться стационарным и обратимым за исключением ситуации, когда . В последнем случае процесс является только либо стационарным, либо обратимым.

При 0 < d < 1/2 процесс ARFIMA (0, d,0) представляет собой стационарный процесс с долгой памятью и может быть полезен при моделировании долговременной устойчивости. Корреляции и частные корреляции являются положительными и спадают монотонно гиперболически к нулю при увеличении лагов. СП сконцентрирована на низких частотах.

При d = 0 процесс ARFIMA (0,0,0) представляет собой белый шум с нулевой корреляцией и постоянной СП.

При -1/2 < d < 0 процесс ARFIMA (0, d,0) имеет короткую память и является неустойчивым. Корреляции и частные корреляции в этом случае все становятся отрицательными (за исключением единичного значения корреляций при нулевом лаге) и спадают монотонно гиперболически до нуля. СП сосредоточена в высокочастотной области и является возрастающей функцией частоты.

При d = - 1/2 процесс ARFIMA (0, -1/2, 0) - стационарный, но необратимый, поэтому предсказания процесса не могут быть выражены через прошлые значения ряда. СП процесса стремится к нулю при ω→ 0.

При d = 1/2 процесс ARFIMA (0, 1/2, 0) имеет СП вида S (ω) = 1 / [2 sin (0,5 ω)] ~ ω^-1 при ω→ 0. Следовательно, в этом случае процесс представляет собой дискретный шум типа 1/ f.

Более важный и интересный класс процессов получается в ситуации, когда в модели ARFIMA параметры p и q не равны нулю. Такая модель описывается выражением (3.3), но показатель d может принимать дробные значения. На практике наиболее интересные процессы имеют место при малых значениях параметров p и q, поэтому рассмотрим более детально модели ARFIMA ( 1, d, 0) и ARFIMA (0, d, 1).

Например, процесс ARFIMA (1, d,0) определяется как

(1 - ф B) (1 – B) ^d X_t = a_t.

Обозначив Y_t = (1 - ф B) X_t, получаем, что (1 – B) ^d Y_t = a_t. Таким образом, процесс { Х _t } является процессом авторегрессии первого порядка с искажениями, обусловленными процессом ARFIMA (0, d,0). Можно ожидать, что долгосрочное поведение процесса { Х _t } будет аналогичным процессу { Y_t }, но в краткосрочном режиме изменение процесса { Х _t } зависит от значения параметра . Для стационарности и обратимости процесса { Х _t } примем, что и .

Для анализа процесса { Х _t } наибольшее значение имеют спектральная плотность и корреляционная функция. Для этих характеристик в [11] найдены следующие выражения:

· спектральная плотность

· корреляционная функция

где - гипергеометрическая функция.

Из приведенных формул следует, что в низкочастотной области СП спадает обратно пропорционально частоте. При больших лагах корреляционная функция также уменьшается, но на характер ее изменения влияет .

Процесс ARFIMA (0, d,1) имеет следующий вид

(1 – B) ^d X_t = (1 - θ B) a_t,

который можно рассматривать как процесс скользящего среднего первого порядка от дробно дифференцированного белого шума.

Процесс является стационарным и обратимым при и .

СП процесса { Х _t } в низкочастотной области определяется в виде

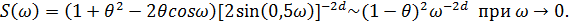
При больших лагах корреляционная функция процесса { Х _t } равна

где

Как видно из приведенных формул, характер спадания определяется не только частотой и лагом, но также и величиной параметра .

Проведем сравнение корреляционных функций двух моделей: ARFIMA (1, d,0) при d = 0,2 и = 0,366 и ARFIMA (0, d,1) при d = 0,2 и = -0,508 (рис.3.25).

Рис.3.25. Сравнение корреляционных функций процессов

ARFIMA (1, d,0) и ARFIMA (0, d,1)

Из графиков, приведенных на рис.3.25, следует, что процесс ARFIMA (0, d,1) спадает более быстро, чем процесс ARFIMA (1, d,0), но при увеличении лага корреляции становятся все более сходными, и доминирует процесс долговременной памяти.

В общем случае в модели ARFIMA(p, d, q), описываемой выражением (3.3), все корни полиномов (B), θ(B) лежат вне единичного круга. Соображения при выборе этого семейства процессов для целей моделирования заключаются в том, что эффект параметра d на разнесенные наблюдения спадает гиперболически при увеличении лага, в то время как эффекты параметров ф и θ уменьшаются экспоненциально. Таким образом, параметр d может быть выбран для описания корреляционной структуры временных рядов с большими лагами, а параметры ф и θ - для корреляционной структуры с малыми лагами.

Процесс X_t для случая d ≠ 0 можно охарактеризовать как интегрированный порядка d и обозначить его как I (d). АКФ будет демонстрировать очень медленную скорость спадания. Для - 0,5 < d < 0,5 процесс является стационарным, в то время как d < 1 подразумевает в среднем возвращение в прежнее состояние. Для процесса I (d) спектральная плотность такова, что S (0) = 0 для d < 0 и S (0) → ∞ для d > 0. Для малых значений частоты аппроксимация при d > 0 приводит к соотношению S (ω) ~ ω^-2 ^d; в то же время условие d > 0,5 определяет процесс с бесконечной дисперсией.

В работе [15] рассмотрены условия существования стационарного решения процесса ARFIMA (p, d, q) общего вида, которые сводятся к следующим. Допустим, что полиномы ф (B) и θ(B) не имеют общих корней, а параметр Тогда

а) если нули ф (B) лежат вне единичного круга { z: | z |=1}, то существует единственное стационарное решение уравнения (3.3) в виде

где ψ (z) = (1 – z)^{- d} θ(z) / ф (z).

б) если нули ф (B) лежат вне замкнутого единичного круга { z: | z | ≤1}, то решение X_t является каузальным (причинным).

в) если нули ф (B) лежат вне замкнутого единичного круга { z: | z | ≤1}, то решение X_t является обратимым.

Напомним, что линейный процесс можно представить в следующем виде (при нулевом математическом ожидании)

(3.37)

где ψ ₀ = 1; { a_t } - белый шум с дисперсией σ², обладает свойством каузальности, так как X_t основывается только на текущих и прошлых значениях входного шума.

Линейный процесс (3.37) является обратимым, если существует последовательность коэффициентов {π _j } таких, что

(3.38)

Из (3.38) при допущении, что π₀ = -1, процесс X_t может быть выражен как

(3.39)

При условии, что процесс ARFIMA (p, d, q) является стационарным, каузальным и обратимым, он может быть представлен в виде

= ψ (B) a_t и

Параметрические выражения для весов при представлении модели ARFIMA (p, d, q) в виде бесконечной авторегрессии и бесконечного скользящего среднего определяются достаточно сложными формулами через гипергеометрическую функцию, поэтому здесь ограничимся предельными случаями [14]. Коэффициенты моделей скользящего среднего МА (∞) ψ _j и авторегрессии AR (∞) π _j определяются следующими выражениями при j → ∞

где Г(d) - гамма-функция.

Для АКФ справедливо следующее выражение

(3.40)

Используя аппроксимацию гамма-функции при больших значениях аргумента в виде

получим, что при больших лагах АКФ гиперболически спадает, принимая вид

(3.41)

Отметим, что для стационарной модели ARMA при значительных лагах АКФ изменяется по соотношению

(3.42)

откуда видно, что в последнем случае значения коэффициентов автокорреляции спадают экспоненциально и быстрее, чем эти же коэффициенты по формуле (3.41).

СП на низких частотах определяется как

Подводя итог рассмотрению модели класса ARFIMA (p, d, q), отметим ее полезность во многих задачах прогнозирования временных рядов. По сравнению с существующими моделями долговременной устойчивости класс ARFIMA (p, d, q) является более гибким при моделировании долговременных и кратковременных характеристик стохастических процессов.