При разработке моделей ВР приходится принимать решение о принадлежности рассматриваемых рядов классам, имеющим только детерминированный тренд (TS -модель) или стохастический тренд, возможно, вместе с детерминированным, (DS -модель). Проблема отнесения ВР к одному из указанных классов привлекает повышенное внимание специалистов-аналитиков в экономической сфере. Поскольку траектории TS - и DS - рядов существенно различаются между собой, вынесенное суждение о принадлежности анализируемого ряда выделенным классам важно при построении долгосрочных моделей прогнозирования.
Линия тренда у TS -рядов представляет собой определенную осевую линию, относительно которой реальная траектория ряда совершает флуктуации с достаточно высокой частотой. Траектория DS -рядов вследствие наличия стохастического тренда (кроме детерминированного) колеблется с низкой частотой, пребывая весьма долго выше или ниже осевой линии тренда, что приводит, по сути дела, к тому, что линия детерминированного тренда перестает играть роль «центра притяжения» флуктуаций.
В TS -рядах влияние предыдущих воздействий ослабевает с течением времени, а в DS - рядах подобного затухания нет, поэтому каждое отдельное возмущение оказывает одинаковое влияние на все последующие значения ряда. При анализе рядов с выраженным трендом ранее было принято производить оценивание и выделение детерминированного тренда, а затем - подбор модели (например, ARMA) к ряду остатков. После введения Боксом и Дженкинсом моделей класса ARIMA анализ рядов с трендом стал проводиться посредством перехода к стационарности через первые или вторые разности. Однако дальнейшие исследования показали, что произвольный выбор одного из этих двух способов «остационаривания» ряда (вычитанием тренда или расчетом первых разностей) может привести к неправильным выводам.
Было показано [6], что остационаривание DS -ряда через вычитание тренда изменяет спектр ряда, формируя ложную периодичность (ложные длиннопериодные циклы), которая может быть ошибочно истолкована как проявление определенного экономического цикла. С другой стороны, взятие первых разностей TS -модели приводит к «передифференцированному» ряду, который, являясь стационарным, обладает некоторыми нежелательными последствиями: в частности, появляется паразитная автокоррелированность соседних значений продифференцированного ряда (в спектре доминируют короткие циклы).
Детрендированный DS -ряд показан на рис.3.14, а его спектральная плотность - на рис.3.19.а. Как видно из последнего рисунка, на графике спектральной плотности имеется явно выраженный максимум, который свидетельствует о наличии циклов в DS –ряде (см.рис.3.14).

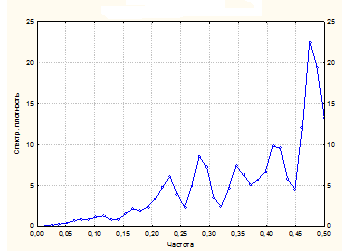
а) б)
Рис.3.19. Спектральная плотность детрендированного DS -ряда (а) и дифференцированного TS -ряда (б)
Спектральная плотность дифференцированного TS-ряда приведена на рис.3.19.б, из которого видно наличие нескольких выбросов на графике плотности, что говорит о присутствии коротких циклов в ряду первых разностей TS -модели (см.рис.3.15).
Таким образом, без выяснения принадлежности ряда к одному из выделенных классов (TS - или DS – моделей) оказывается трудным принять решение об адекватной модели анализируемого ряда. Для решения задачи различения указанных моделей было предложено множество процедур классификации, но приемлемого результата пока не достигнуто. Вследствие этого аналитики обычно используют при исследовании рядов на принадлежность их к классу TS или DS не один, а несколько критериев и подкрепляют выводы, полученные с использованием формальных критериев (с установленными уровнями значимости), графическими процедурами.
В большинстве критериев, предложенных для различения DS и TS гипотез, в качестве нулевой (исходной) берется гипотеза DS, а TS -гипотеза является альтернативной. При этом нулевая DS -гипотеза формулируется как «гипотеза единичного корня» (unit root), т.е. как гипотеза о наличии корня z = 1 в уравнении  (z) = 0, где
(z) = 0, где  (B) – многочлен от оператора обратного сдвига B в авторегрессионном представлении для ряда Xt в виде
(B) – многочлен от оператора обратного сдвига B в авторегрессионном представлении для ряда Xt в виде 
Критерии, в которых за исходную (нулевую) гипотезу берется гипотеза TS, служат скорее для подтверждения результатов проверки DS -гипотезы. В этом случае вместо проверки гипотезы единичного корня для самого ряда X t проверяется гипотеза о наличии единичного корня z = 1 в уравнении θ(z)=0, где θ(В) – многочлен от оператора обратного сдвига В в представлении в виде процесса скользящего среднего D Хt = θ(B) a t ряда разностей D X t = X t - X t- 1 исходного процесса X t.
Рассмотрим наиболее часто используемый метод, который позволяет формально проводить различие между рядами типа TS и DS [5]. Обратимся к модели следующего вида
Xt = α + ρ Xt – 1 +β t + at. (3.14)
Модель (3.14) вобрала характерные черты обоих рядов TS и DS типов, выражаемые формулами (3.11), (3.12) Тогда гипотезы о характере ряда можно записать в виде простых гипотез о параметрах рядов, а именно:
H 0: ряд принадлежит типу DS, если ρ = 1; β = 0;
H 1: ряд принадлежит типу TS, если |ρ| < 1 (при таком условии at является не просто белым шумом, а некоторым стационарным рядом).
Нулевая гипотеза относится к классу общих линейных гипотез. При традиционном подходе для ее проверки нужно оценить две регрессии:
Xt = α + ρ Xt – 1 +β t + at и Xt = α + Xt – 1 + at.
Затем необходимо проверить значимость разности остаточных сумм квадратов с использованием F -статистики. Рассматриваемый далее тест был впервые предложен Дики-Фуллером и носит их имя. Под критерием Дики-Фуллера в действительности понимается группа критериев, объединенных одной идеей. В этих критериях нулевой является гипотеза о том, что исследуемый ряд Хt принадлежит классу DS (DS -гипотеза); альтернативная гипотеза – исследуемый ряд принадлежит классу TS (TS -гипотеза). Критерий Дики-Фуллера фактически предполагает, что наблюдаемый ряд описывается моделью авторегрессии первого порядка (возможно, с поправкой на линейный тренд).
Вначале обратимся к более простой версии модели (3.14), которая выражается как
Xt = α + ρ Xt – 1 + at, (3.15)
т.е. без включения линейного тренда. В этом случае указанные выше гипотезы принимают вид
H 0: ряд принадлежит типу DS, если ρ = 1;
H 1: ряд принадлежит типу TS, если |ρ| < 1.
Тогда можно проверить гипотезу о том, что ρ = 1 при помощи t -статистики. Уравнение (3.15) модифицируем следующим образом: после вычитания из обеих частей Xt – 1, получим уравнение в разностях вида
Δ Xt = α + (ρ – 1) Xt – 1 + at, t = 1,..., N. (3.16)
Положим ρ – 1 = γ, тогда последнее уравнение и проверяемые гипотезы имеют вид
Δ Xt = α + γ Xt – 1 + at, (3.17)
H 0: γ = 0;
H 1: γ < 0.
В классической линейной регрессии для проверки такой гипотезы применяется односторонняя t -статистика. Для проверки гипотезы H 0 следует найти методом наименьших квадратов (МНК) оценки α*, γ* параметров уравнения (3.17) α и γ. Далее необходимо проверить условие |γ*| < σγ* q 100 p /2, где σγ* - оценка СКО параметра γ; q 100 p /2 - квантиль распределения Стьюдента с N – 1 степенями свободы и уровнем значимости р.
При выполнении неравенства гипотеза H 0 не отвергается на уровне значимости р. Однако воспользоваться таким общепринятым правилом проверки гипотез в данном случае не представляется возможным, так как величина γ*/ σγ* не является распределенной по закону Стьюдента с N – 1 степенями свободы из-за того, что она порождена DS -процессом. Эта величина подчиняется распределению, которое также предложили Дики-Фуллер. Вследствие указанного здесь критической точкой не может являться 100 p /2-процентный квантиль Стьюдента и необходимы поиски иной критической точки, соответствующей распределению Дики-Фуллера. Такие критические точки были найдены методом Монте-Карло, а тест, основанный на сопоставлении величины γ*/ σγ* с соответствующими квантилями, называется тестом Дики-Фуллера.
Аналогичная ситуация возникает и при рассмотрении модели более общего вида
Δ Xt = α + γ Xt – 1 +β t + at. (3.18)
Соответствующие гипотезы принимают вид
H 0: β = 0; γ = 0 → модель DS;
H 1: γ < 0 → модель TS.
Для проверки гипотезы H 0 следует найти МНК-оценки параметров α, γ, β уравнения (3.18), вычислить коэффициент детерминации  , сформировать статистику
, сформировать статистику
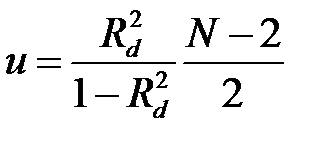
и сравнить ее с квантилем распределения Фишера up, взятым при уровне значимости р и числами степеней свободы, равными 2 и N - 2. При выполнении неравенства u < up в соответствии с традиционным статистическим подходом гипотеза H 0 не отвергается как неправильная. Однако, как и в случае использования распределения Стьюдента, общепринятый метод проверки гипотез здесь не годится, так как статистика u в случае DS -процесса не подчиняется распределению Фишера. Вследствие этого необходим расчет критических точек для величины u в зависимости от объема выборки и доверительной вероятности. Такие критические точки приведены в табл.3.3 вместе с F -статистикой Фишера.
Таблица 3.3 Критические точки распределений Дики-Фуллера и Фишера
| Объем выборки | Распределение Дики-Фуллера | Распределение Фишера |
| 25 50 100 ∞ | 7,24 6,73 6,49 6,25 | 3,44 3,20 3,09 3,00 |
Из сопоставления табличных данных видны те последствия, которые могут возникнуть при использовании в качестве критических точек квантилей распределения Фишера. Например, если при объеме выборки N = 25 окажется 3,44 < u < 7,24 и при этом руководствоваться общими статистическими рекомендациями, то гипотезу H 0 следует отвергнуть в пользу гипотезы H 1. Если же ориентироваться на критическую точку, равную 7,24, что в данном случае и надо делать, то гипотеза H 0 сохранит свой приоритет.
На рис.3.20, заимствованном из [5], схематично показаны графики плотностей вероятностей распределений Фишера и Дики-Фулера. Из рис.3.20 видно, что большая доля вероятности распределения Дики-Фулера расположена значительно правее по сравнению с распределением Фишера. Это означает, что в большинстве случаев применение стандартной F -статистики ведет к появлению ошибки, например: если F -статистика попадет в область (а, b), то считается, что ряд относится к типу TS, в то время как ряд принадлежит классу DS.

Рис.3.20. Плотности вероятности распределений Фишера и Дики-Фулера
Необходимо обратить внимание на то, что при использовании распределения Дики-Фулера критические точки зависят не только от объема выборки и уровня значимости, но и от количества регрессоров, которые включены в исследуемую модель.
Например, если в уравнении (3.17) принять α ≠ 0, то получится одно распределение Дики-Фулера с соответствующими ему критическими точками. В противном случае (α = 0) имеем иное распределение Дики-Фулера с другими критическими точками. Аналогичная ситуация складывается и для уравнения (3.18): распределение Дики-Фулера и критические точки являются различными в зависимости от того, включены или нет в модель параметры α, β. Таким образом, под критерием Дики-Фуллера в действительности понимается группа критериев, объединенных одной идеей. Поскольку заранее невозможно однозначно определить, какие именно регрессоры должны быть включены в модель, применение тестов Дики-Фуллера приобретает итеративный характер, направленный на совершенствование модели путем включения в нее новых регрессоров или исключения старых, не прошедших соответствующие тесты.
Еще раз подчеркнем, что в критериях Дики-Фуллера проверяемой (нулевой) является гипотеза о том, что исследуемый ряд x t принадлежит классу DS (DS -гипотеза); альтернативная гипотеза – исследуемый ряд принадлежит классу TS (TS -гипотеза). Критерий Дики-Фуллера фактически предполагает, что наблюдаемый ряд описывается моделью авторегрессии первого порядка AR (1) (возможно, с поправкой на линейный тренд). Критические значения зависят от того, какая статистическая модель оценивается и какая вероятностная модель в действительности порождает наблюдаемые значения. При этом рассматриваются следующие три пары моделей (SM – статистическая модель, statistical model; DGP – модель порождения данных, data generating process) [6].
1) Если ряд Xt имеет детерминированный линейный тренд (наряду с которым может иметь место и стохастический тренд), то в такой ситуации берется пара
SM: Δ Xt = α + γ Xt – 1 +β t + at, t = 2,..., T,
DGP: Δ Xt = α + at, t = 2,..., T.
В анализируемом варианте статистическая модель определяется уравнением (3.18); модель порождения данных - случайное блуждание с дрейфом. В обоих случаях at – независимые случайные величины, имеющие одинаковое нормальное распределение с нулевым математическим ожиданием.
С помощью МНК оцениваются параметры данной статистической модели, и вычисляется значение t -статистики t γ для проверки гипотезы H 0: γ = 0. Полученное значение сравнивается с критическим уровнем t кр, рассчитанным в предположении, что наблюдаемый ряд в действительности порождается данной моделью DGP. Проверяемая DS -гипотеза отвергается, если t γ < t кр.
2) Если ряд Xt не имеет детерминированного тренда (но может обладать стохастическим трендом) и имеет ненулевое математическое ожидание, то берется пара
SM: Δ Xt = α + γ Xt – 1 + at, t = 2,..., T, (3.19)
DGP: Δ Xt = at, t = 2,..., T.
Методом наименьших квадратов оцениваются параметры данной SM и вычисляется значение t -статистики t γ для проверки гипотезы H 0: γ = 0. Полученное значение сравнивается с критическим уровнем t кр, рассчитанным в предположении, что наблюдаемый ряд в действительности порождается данной моделью DGP (случайное блуждание без сноса). DS -гипотеза отвергается, если t γ < t кр.
3) Наконец, если ряд Xt не имеет детерминированного тренда (но в ряде может присутствовать стохастический тренд) и имеет нулевое математическое ожидание, то берется пара
SM: Δ Xt = γ Xt – 1 + at, t = 2,..., T, (3.20)
DGP: Δ Xt = at, t = 2,..., T.
Посредством МНК оцениваются параметры данной SM, и вычисляется значение t -статистики t γ для проверки гипотезы H 0: γ = 0. Полученное значение сравнивается с критическим уровнем t кр, рассчитанным в предположении, что наблюдаемый ряд в действительности порождается данной моделью DGP (случайное блуждание без сноса). DS -гипотеза отвергается, если t γ < t кр.
Пороговые значения t кр критерия Дики-Фуллера можно рассчитать по формуле [3]
t кр = k 0 + k 1 / (N + 1) + k 2 / (N + 1)2, (3.21)
в которой параметры k 0, k 1, k 2 зависят от уровня значимости р и сложности исследуемой модели. Указанные параметры для рассмотренных моделей приведены в табл.3.4.
Таблица 3.4 Значения параметров k 0, k 1, k 2
| Параметры | Модель (3.18) | Модель (3.19) | Модель (3.20) | |||
| р = 0,01 | р = 0,05 | р = 0,01 | р = 0,05 | р = 0,01 | р = 0,05 | |
| k 0 | -3,96 | -3,41 | -3,43 | -2,86 | -2,57 | -1,94 |
| k 1 | -8,35 | -4,04 | -6,0 | -2,74 | -1,96 | -0,40 |
| k 2 | -47,44 | -17,83 | -29,25 | -8,36 | -10,04 | 0 |
3.5. Дробно - интегрированная модель ARFIMA
В рассмотренной выше модели ARIMA, выражаемой равенством (3.3)
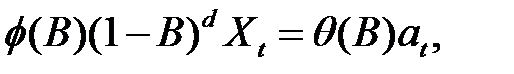
показатель d принимает целочисленные значения, равные 1 или 2. По существу, параметр d характеризует порядок разности при приведении нестационарного ряда к стационарному виду. На практике значения d, превышающие 2, обычно не используются.
Однако существует разновидность рядов, у которых этот показатель принимает дробное значение. Разработка такой авторегрессионной дробно интегрированной модели скользящего среднего (autoregressive fractionally integrated moving average - ARFIMA) приводит к более гибкому и полному классу моделей ВР, который расширяет методологию Бокса-Дженкинса. Перед тем, как перейти к описанию модели ARFIMA, определим класс моделей с долгой памятью.






