Вопрос о стационарности или нестационарности модели, порождающей наблюдаемый ряд, привлекает к себе постоянное внимание на протяжении многих лет. Как следует из теоремы Вольда, модели типа ARMA охватывают все стационарные процессы. С нестационарными процессами ситуация иная: фактически рассматриваются только частные виды нестационарных временных рядов. Например, рассмотренный выше процесс ARIMA (p, d, q), который является нестационарным, может быть приведен к стационарному виду после применения d раз операции взятия последовательных разностей.
Напомним, что исходной информацией при построении модели является экспериментально зарегистрированная реализация ряда, которая обычно представлена в единственном числе. Такой наблюдаемый ряд отождествляется с реализацией некоторого случайного процесса, взятого в дискретные равноотстоящие моменты времени. Например, если w (t) - реализация процесса W (t), то wn = w (tn), n =0,1,…, N. Относительно процесса W (t) вводится допущение о возможности представления этого процесса в виде аддитивной смеси структурно детерминированной g (t, a) и стохастической составляющей s (t), т.е.
W (t) = g (t, a) + s (t). (3.10)
Первый компонент этой смеси определяется функцией аргумента t вектора неизвестных параметров a. Эта структурно детерминированная составляющая обобщает такие понятия ВР как тренд, сезонные и циклические колебания и, в общем случае, характеризует долговременные характеристики ряда.
Второй компонент отражает стохастическую природу ВР и может быть представлен какой-либо моделью типа AR (p), MA (q), ARMA (p, q). Математическое ожидание такого ряда определяется детерминированной составляющей g (t, a), и формально ряд оказывается нестационарным. Однако путем вычитания из наблюдаемых данных функции g (t, a) этот ряд становится стационарным относительно математического ожидания. По установившейся в последние годы терминологии такие ряды относят к классу TS -рядов (trend stationary series - стационарные относительно тренда ряды).
Возможна ситуация, когда детерминированная составляющая в выражении (3.10) отсутствует, но визуальный анализ ряда создает иллюзию ее присутствия (см. рис. 3.5, 3.7, 3.9, 3.11). Подобные ряды могут быть превращены в стационарные посредством взятия d разностей исходного ряда. В таких ситуациях говорят, что ряд характеризуется стохастическим трендом, и подобные временные ряды выделяют в отдельный класс DS –рядов (difference stationary series - стационарные после дифференцирования ряды).
Поясним более подробно различие между указанными двумя типами ВР. Рассмотрим две модели нестационарных рядов.
Первая модель: TS -ряд. Положим, что ряд имеет линейный тренд и описывается следующим образом
Xt = α + β t + at, t = 1,..., T, (3.11)
т.е. на детерминированный линейный тренд накладываются случайные ошибки в виде белого шума.
Для этого ряда можно записать, что Δ Xt = Xt - Xt – 1 = β + (at - at - 1 ). Поскольку at - стационарный процесс, то его первая разность также описывается стационарной моделью, а математическое ожидание приращения Е ( Δ Xt) = β.
Вторая модель: DS –ряд. Здесь ряд представляет собой случайное блуждание с дрейфом, которое имеет вид
Xt = α + Xt – 1 + at, t = 1,..., T. (3.12)
В этом случае приращение ряда определяется как Δ Xt = Xt - Xt – 1= = α + at с математическим ожиданием приращения, равным Е( Δ Xt) = α. В данной модели процесс Xt можно представить следующим образом
Xt = α + Xt – 1 + at = α + (α + Xt – 2 + at - 1) + at = 2α + Xt – 2 + at – 1 + at =
=... = at +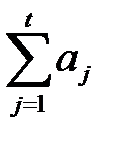 
. (3.13)
Из последнего равенства следует, что ряд Xt имеет и детерминированный, и стохастический тренды.
Сопоставление двух рядов (3.11) и (3.12) позволяет сделать вывод об их сходстве и различии: оба ряда имеют линейный тренд, но отличаются случайной частью. В первой модели случайная часть - текущие возмущения at, во второй модели случайная часть - накопленные возмущения на предыдущих шагах .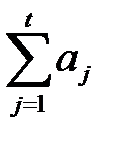
Проведем операцию детрендирования (устранения тренда) для обоих рядов.
Для первого ряда (3.11) получаем, что Xt 0 = Xt – (α + β t) = at, т.е. детрендированный ряд в этом случае получается стационарным.
Во втором случае из выражения (3.13) имеем: Xt 0 = Xt - at = 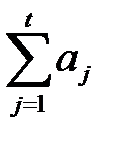, что свидетельствует о нестационарности полученного ряда. Следовательно, операция детрендирования приводит к разным типам моделей ВР: стационарному и нестационарному.
Однако операция перехода от исходных рядов к рядам разностей (в теории ВР такую операцию называют дифференцированием) приводит к стационарности в обоих случаях. Два продифференцированных ряда Δ Xt - стационарны. Первый продифференцированный ряд Δ Xt = β + (at - at - 1 ) относится к классу МА (1) и имеет математическое ожидание, равное β. Второй продифференцированный ряд Δ Xt = α + at относится к типу МА (0) с математическим ожиданием, равным α.
Таким образом, в отличие от детрендирования операция дифференцирования приводит к стационарному ряду в обоих случаях. Основная разница между этими двумя классами рядов состоит в том, что из TS -ряда путем детрендирования можно получить стационарный ряд, а для DS –ряда такая операция не приводит к нужному результату, так как последний ряд содержит стохастический тренд.
В качестве примера рассмотрим имитацию рядов типа TS и DS, определяемых, соответственно, выражениями (3.11) и (3.12). При моделировании примем для TS -ряда: TSt = 1 +0,5 t + at, at ~ N (0,1), а для DS –ряда: DSt = 0,1 + DSt – 1 + at, at ~ N (0;0,25). Результаты моделирования приведены на рис.3.13.
Рис.3.13. Результаты моделирования рядов типа TS (слева) и DS (справа)
Выполним для полученных рядов операцию детрендирования, т.е. вычитания из смоделированных значений величин тренда, для чего вначале найдем по результатам имитации уравнения линейной регрессии. Представленные итоговые таблицы (табл.3.1 и 3.2) оценок параметров регрессии позволяют выписать трендовые уравнения следующего вида.
Для TS -ряда: Xt = 0,78 + 0,50 t; для DS –ряда: Xt = -0,075 + 0,093 t.
Таблица 3.1 Расчет уравнения регрессии для TS -ряда
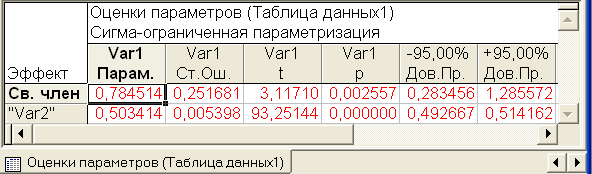
Таблица 3.2 Расчет уравнения регрессии для DS -ряда
Отметим, что для DS –ряда свободный член уравнения оказался незначимым при уровне значимости р = 0,05.
Детрендированные ряды обоих типов показаны на рис.3.14.
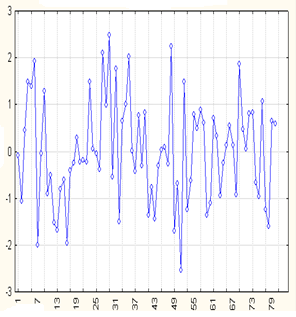
Рис.3.14. Детрендированные ряды (слева - TS -ряд; справа - DS –ряд)
Как видно из рис.3.14, изменение детрендированного TS -ряда характерно для стационарного ВР. В то же время DS –ряд после операции вычитания тренда демонстрирует наличие некоторой сезонности с достаточно большим периодом. Такая особенность этого ряда отмечалась ранее в работах [5,6]: в результате очистки ряда от детерминированного тренда могут возникать систематические колебания, которые представляют собой циклы с большим периодом. Таких циклов не было у исходного ряда, вследствие чего можно совершить ошибку, признав существование некой периодичности (ложная периодичность) и наличия возможного экономического цикла.
Перейдем к формированию рядов первых разностей. На рис.3.15 приведен график, построенный для первых разностей TS -ряда. С целью подбора подходящей модели на рис.3.16 показаны рассчитанные для этого случая АКФ и ЧАКФ. Как видно из графиков коррелограмм, трудно отдать предпочтение какой-либо конкретной модели: значимые выбросы имеются и на графике АКФ, и на графике ЧАКФ, поэтому выбор между моделями типов AR или MA нельзя сделать однозначным. Необходимо учесть, что при практической реализации различных рекомендаций о выборе приемлемых моделей нет гарантии правильности принимаемых решений, поскольку данные наблюдений и их характеристики не всегда явным образом соответствуют свойствам их теоретических аналогов.
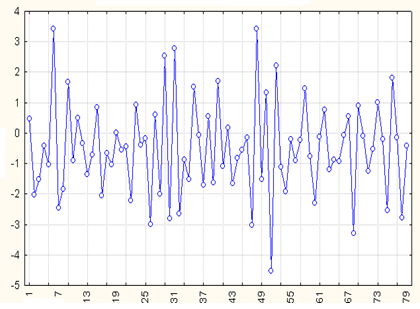
Рис.3.15. График первых разностей TS -ряда
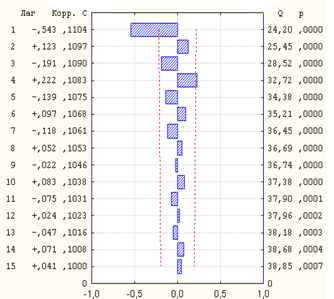
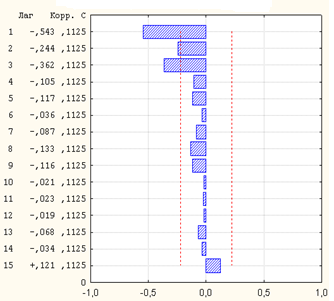
а) б)
Рис.2.16. АКФ (а) и ЧАКФ (б) первых разностей TS -ряда
Результаты аналогичной процедуры для DS –ряда приведены на рис.3.17, 3.18. Поскольку значения АКФ и ЧАКФ не выходят за пределы доверительного интервала, можно считать, что первые разности DS -ряда представляют собой белый шум.
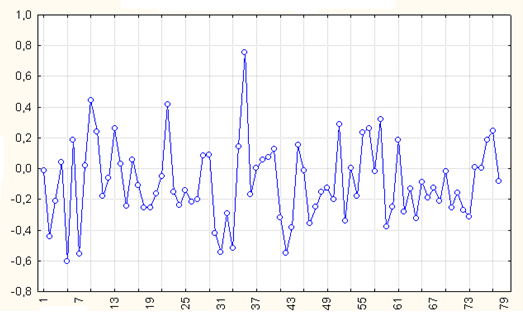
Рис.3.17. График первых разностей DS -ряда
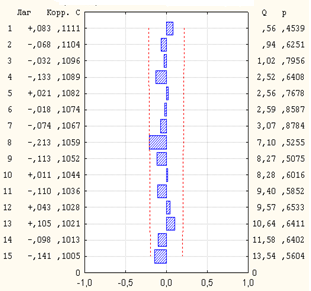
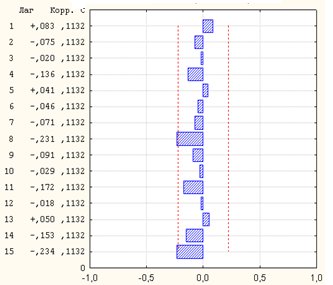
а) б)
Рис.3.18. АКФ (а) и ЧАКФ (б) первых разностей DS -ряда
