Модель авторегрессии - проинтегрированного скользящего среднего

Для ряда, приводимого к стационарному виду, предложено название c аббревиатурой ARIMA, где к уже известному обозначению ARMA добавлена буква I (Intergrated - проинтегрированный). Принято обозначать количество операций взятия разностей буквой d, что приводит к такому обозначению модели: ARIMA (p, d, q). Бесконечно малая разность - это дифференциал, а обратный переход от дифференциала определяет интегрирование. Вследствие этого модель ARIMA (p, d, q) получила название процесса авторегрессии - интегрированного скользящего среднего. Показатели в обозначении модели ARIMA (p, d, q) относятся: p - к авторегрессионному процессу AR (p); d - к степени интеграции; q - к процессу скользящего среднего MA (q).

Рассмотрим более подробно появление такой модели. Ранее было показано, что процесс ARMA является стационарным, если корни уравнения 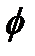(B) = 0 лежат вне единичного круга, и нестационарным в случае, когда корни находятся внутри единичного круга (п. 2.3). Единственный нерассмотренный случай: корни уравнения 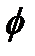(B) = 0 лежат на единичной окружности.

Введем в рассмотрение модель следующего вида

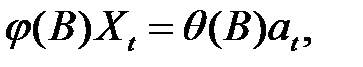(3.2)

где в отличие от равенства (2.25) j(В) - нестационарный оператор авторегрессии порядка p + d, такой, что d корней уравнения j(В) = 0 равны единице, а остальные р корней лежат вне единичного круга; оператор же скользящего среднего q(В) по-прежнему имеет вид (2.16), т.е. обладает порядком q и является обратимым (все его корни лежат вне единичного круга).

Тогда уравнение (3.2) можно записать в виде

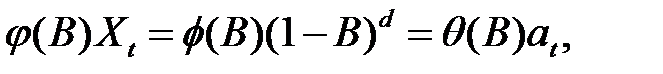
где - стационарный порядка р оператор авторегрессии (т.е. с корнями вне единичного круга).

Если ввести оператор разности Δ X_t = X_t - X_t _- ₁ = (1 – B) X_t, то j(В) запишется как 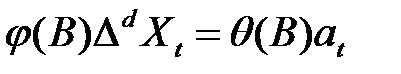и модель (3.2) можно представить в виде

(3.3)

Эквивалентное определение этого процесса описывается двумя уравнениями

(3.4)

(3.5)

Иначе говоря, d -я разность ряда Х _t, вычисляемая по формуле (3.5), удовлетворяет уравнению (3.4), поэтому является уже стационарным обратимым процессом ARMA (p, q).

Таким образом, процесс ARIMA (p, d, q), описываемый уравнением (3.3), можно получить d -кратным суммированием (или интегрированием) процесса { w _t}, являющегося в соответствии с (3.4) процессом ARMA (p, q). Из выражения (3.3) следует, что процесс { X_t } становится стационарным, только в том случае, когда d = 0. При этом общая модель ARIMA (p, d, q) сводится к смешанной стационарной модели ARMA (p, q). Тем самым модель ARIMA (p, d, q) охватывает широкий класс как стационарных (при d =0), так и нестационарных (при d ³ 1) процессов. На практике d обычно принимается равным 0, 1 или максимум 2.

Отметим, что при d ³ 1 можно добавить произвольный полиномиальный тренд степени (d – 1) к процессу { X_t }, не нарушая уравнения (3.3). Вследствие этого модели класса ARIMA (p, d, q) являются полезными для представления данных с трендом.

Рассмотрим частные случаи модели ARIMA (p, d, q).

1. ARIMA (0, 1,0): модель приводится к виду X_t = X_t _– ₁ + a_t, которая представляет собой модель случайного блуждания (3.1), проанализированную выше.

2. ARIMA (0, 2,0): здесь модель приобретает вид

X_t = 2 X_t _– ₁ - X_t _– ₂ + a_t. (3.6)

График этого процесса при X ₀ = 0, a_t ~ N (0,1) показан на рис.3.5. Соответствующие АКФ и ЧАКФ модели ARIMA (0, 2,0) приведены на рис.3.6.

Рис.3.5 График процесса ARIMA (0, 2,0)

а) б)

Рис.3.6. Выборочные АКФ (а) и ЧАКФ (б) модели ARIMA (0, 2,0)

3. ARIMA (1, 1,0): из выражения (3.3) получаем в этом случае уравнение (1 - (1 – В) X_t = a_t, которое преобразуется к виду

X_t = (1 + ф) X_{t –} ₁ + ф X_{t –} ₂ + a_t. (3.7)

Разыгранная реализация рассматриваемой модели при X ₀ = 0; ф = 0,5; a_t ~ N (0,1) показана на рис.3.7. Выборочные АКФ и ЧАКФ разыгранной модели приведены на рис.3.8.

Рис.3.7. График процесса ARIMA (1, 1,0)

а) б)

Рис.3.8. Выборочные АКФ и ЧАКФ модели ARIMA (1, 1,0)

4. ARIMA (0, 1,1): из формулы (3.3) получаем в этом случае уравнение (1 – B) X_t = (1 – θ B) a_t, которое трансформируется к следующему выражению

X_t = X_t _– ₁ + a_t + θ a_t _{– 1}. (3.8)

Результат моделирования по последней формуле при X ₀ = 0; θ =0,1 показан на рис.3.9.

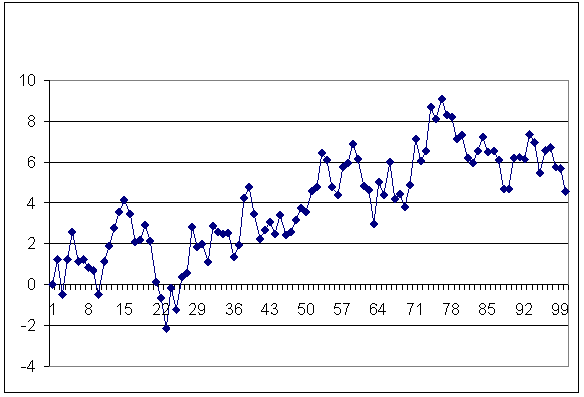
Рис.3.9. График процесса ARIMA (0, 1,1)

Выборочные АКФ и ЧАКФ разыгранной модели приведены на рис.3.10.

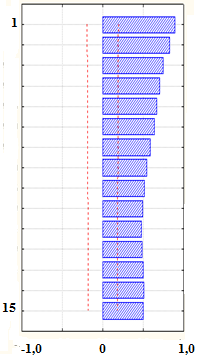
а) б)

Рис.3.10. Выборочные АКФ (а) и ЧАКФ (б) модели ARIMA (0, 1,1)

5. ARIMA (1, 1,1): для этого процесса из уравнения (3.3) получим вначале выражение (1 - (1 – В) X_t = (1 – θ B) a_t, которое затем преобразуем к виду

X_t = (1 + ) X_{t –} ₁ - X_{t –} ₂ + a_t + θ a_{t –} ₁. (3.9)

На рис.3.11 представлен результат моделирования по формуле (3.9) при X ₀ = 0; =0,5; θ =0,5.

Рис.3.11. График процесса ARIMA (1, 1,1)

Выборочные АКФ и ЧАКФ разыгранной модели приведены на рис.3.12.

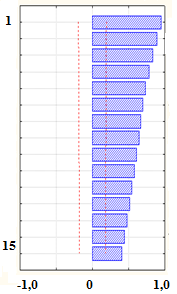
а) б)

Рис.3.12. Выборочные АКФ (а) и ЧАКФ (б) модели ARIMA (1, 1,1)

Рассмотрим вопрос, связанный с идентификацией порядка разности модели ARIMA (p, d, q), который определяется параметром d. Пусть d - неизвестный порядок модели, который нужно оценить. Прежде всего, визуализируем ряд и определим, является ряд стационарным или нет, исходя из графических представлений. Нестационарность ряда часто видна «на глаз», если в ряде имеется ярко выраженный тренд. Наличие тренда - первое свидетельство нестационарности ряда.

Далее имеет смысл посмотреть на амплитуды колебаний на разных участках ряда: возможно, амплитуда колебаний различна для разных частей траекторий. В случае если каждый из отрезков является траекторией стационарного ряда, но с разной дисперсией, то в целом ряд не является стационарным.

Если тренд не выражен отчетливо и нет других особенностей ряда, указывающих на нестационарность, то следует рассмотреть оценку АКФ. Выше было указано, что для стационарной модели, у которой ни один из корней не лежит близко к границе единичного круга, АКФ быстро спадает. При отсутствии тенденции к затуханию АКФ можно говорить о нестационарности ряда, поскольку такое поведение АКФ может рассматриваться как свидетельство того, что существует корень, близкий к единице.

Заметим, что тренд может быть не виден отчетливо на графике, однако нестационарность проявится с помощью критерия поведения АКФ. Таким образом, по графику АКФ можно придти к одному из следующих выводов: ряд стационарен или нестационарен.

В применении к модели ARIMA первый случай означает, что d = 0, поэтому следует перейти к определению остальных параметров модели, т.е. р и q.

При втором выводе следует рассмотреть разность первого порядка наблюдаемого ряда, предполагая, что ряд первых разностей будет стационарным.

К полученному ряду первых разностей вновь применяют критерий стационарности. Опять возможны два вывода. Если приходят к заключению, что ряд первых разностей нестационарен, то берут снова его разности первого порядка и используют критерий стационарности. Так как разности первого порядка взяты последовательно дважды, то это означает, что к исходному ряду применен разностный оператор второго порядка.

На практике процедуру последовательного взятия разностей редко применяют больше двух раз, так как нечасто встречаются модели с порядком разности, большим 2. Процедура заканчивается на шаге k, если преобразованный ряд стал стационарным и d = k.

Отметим, что критерий стационарности носит нестрогий характер, потому что в нем используются не точные автокорреляционные функции, а их оценки. Кроме того, используются не сами оценки, а графики функций, отсюда следует, что критерий допускает довольно широкое толкование и, возможно, найдется несколько приемлемых значений для порядка разности d,что следует учитывать на практике.