Глава 3 Нестационарные временные ряды
3.1. Модель случайного блуждания. 1
3.2. Модель авторегрессии - проинтегрированного скользящего среднего. 5
3.3. Модели идентификации нестационарных временных рядов. 12
3.4. Различение TS - и DS -моделей. 19
3.5. Дробно - интегрированная модель ARFIMA.. 27
3.5.1. Долгая память временного ряда. 28
3.5.2. Свойства модели ARFIMA.. 33
3.5.3. Моделирование процесса ARFIMA.. 42
3.5.4 Реальные процессы с долгой памятью.. 50
3.5.5Оценивание параметров модели ARFIMA.. 52
До сих пор рассматривались стационарные ВР, в которых среднее значение и ковариация между Х t и Х t - l (l - произвольное целое) являлись инвариантными во времени. Рассмотренные выше модели стационарных ВР образуют важный для приложений класс моделей, основанных на предположении, что процесс остается в равновесии относительно постоянного среднего уровня. Однако многие ряды в различных сферах техники, экономики, производства обнаруживают нестационарный характер, в частности, не имеют фиксированного среднего. Тем не менее, их свойства могут быть в некотором смысле однородными. В главе описываются нестационарные ВР, включающие процессы классов ARIMA и ARFIMA (ряд с долгой памятью). Выделяются и анализируются стационарные относительно тренда ряды (TS -ряды) и стационарные после дифференцирования ряды (DS -ряды). Определяются модели идентификации нестационарных ВР, приводятся примеры моделирования нестационарных ВР и рассматриваются реальные ВР, обладающие нестационарностью. Материал главы основан на работах [1-15].
Модель случайного блуждания
Модель случайного блуждания (random walk) часто используется для описания движения биржевых цен. Случайное блуждание (СБ) определяет путь случайной переменной, где каждое изменение не зависит от всех предыдущих изменений и каждое подчиняется идентичному распределению вероятностей. Такая модель является дискретной аппроксимацией броуновского движения.
Независимость в этой модели означает, что изменение в какой-либо момент времени не имеет никакого влияния на все последующие изменения. Это может проявляться в виде нулевой корреляции между следующими друг за другом парами наблюдений. Подидентичностью подразумевается, что каждое из изменений подчиняется одному и тому же распределению вероятностей с одними и теми же параметрами распределения, такими, как средняя величина и среднее квадратическое отклонение.
Модель СБ описывается уравнением
Xt = Xt – 1 + at, (3.1)
где, как и прежде, at - белый шум.
На рис.3.1 представлен график, иллюстрирующий поведение такого процесса. При построении графика начальное значение Х 0 принималось равным нулю, а белый шум разыгрывался как нормально распределенная величина с нулевым средним и единичной дисперсией.
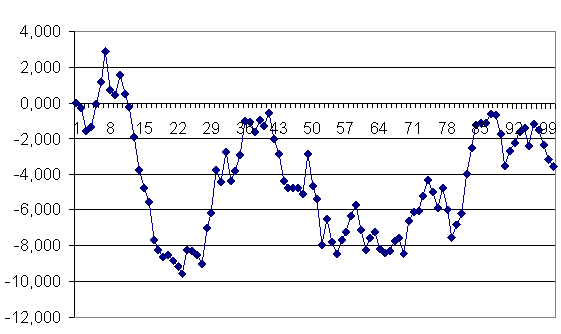
Рис.3.1. Модель случайного блуждания
На рис.3.2 приведены выборочные АКФ и ЧАКФ модели (3.1), вид которых позволяет предположить, что данный процесс описывается моделью AR (1).
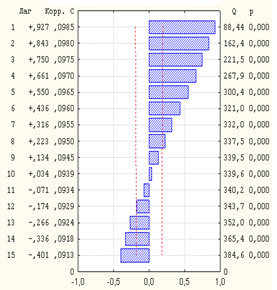
а) б)
Рис.3.2. Выборочные АКФ (а) и ЧАКФ (б) модели случайного блуждания
Рассмотрим модель СБ как специальный случай процесса AR (1) с коэффициентом при Xt – 1, равным единице, т.е.
Xt =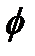 
1 Xt - 1 + at,
где 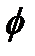1 = 1.
Условие стационарности процесса авторегрессии AR (1) заключается в том, что ׀ 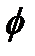1 ׀< 1. Оценим поведение этого процесса при значениях 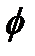1, лежащих вне разрешенного диапазона, например, 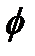1 =1,1 и 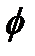1 =1,5. На рис.3.3 показаны сгенерированные модели AR (1) при этих значениях 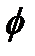1 (значения at разыграны из нормального распределения с нулевым средним и единичной дисперсией). Видно, что изменение этого ряда при выбранных значениях коэффициентов следует, скорее, экспоненциальному закону, т.е. ряд ведет себя как нестационарный.
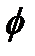1 =1,1 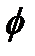1 =1,5
Рис.3.3. Процесс AR (1) с коэффициентами ф 1 =1,1 и ф 1 =1,5
Таким образом, приходим к заключению, что процесс (3.1) является нестационарным ВР.
Пониманию различного поведения реализаций процесса AR (1) (при разных значениях 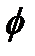1) помогает представление модели в виде
Xt - Xt - 1 = ф 1 Xt - 1 - Xt - 1 + at = (ф 1 -1) Xt - 1 + at или Δ Xt = φ Xt - 1 + at,
где Δ Xt = Xt - Xt - 1; φ = ф 1 -1.
При 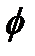1 = 1 имеем φ = 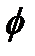1 - 1 = 0, и приращения Δ Xt ряда Xt образуют процесс белого шума, так что условное математическое ожидание (МО) величины Δ Xt при фиксированном (наблюдаемом) значении Xt - 1 = х t - 1 не зависит от х t - 1 и равно нулю. Соответственно, при фиксированном значении Xt - 1 = х t - 1 условное МО случайной величины Xt = Δ Xt + Xt - 1 равно х t - 1 . Если распределение случайной величины at симметрично относительно нуля (которое и использовалось при моделировании), то наблюдаемое значение Xt = х t может с равным успехом оказаться как больше, так и меньше х t - 1. Именно это и определяет блуждающий характер траектории ряда.
При ф 1 > 1 получаем φ = ф 1 - 1 > 0, и условное МО Δ Xt при фиксированном (наблюдаемом) значении Xt - 1 = х t - 1 , равное Е (Δ Xt | Xt - 1 = х t - 1 ) = φ х t - 1, имеет знак, совпадающий со знаком х t - 1. Таким образом, если х t - 1 > 0, то ожидаемое значение следующего наблюдения Xt = х t больше величины х t - 1; в противном случае при х t - 1 < 0 ожидаемое значение следующего наблюдения Xt = х t меньше величины х t - 1. Наличие такого механизма приводит к быстрому и прогрессирующему удалению траектории процесса от начального уровня.
Вновь обратимся к процессу (3.1), который можно представить в следующем виде
Xt = Xt - 1 + at = (Xt - 2 + at - 1) + at = Xt - 2 + at - 1 + at = (Xt - 3 + at - 2) + at - 1 + at =
= Xt - 3 + at - 2 + at - 1 + at =... = X 0 + (a 1 +... + at),
т.е.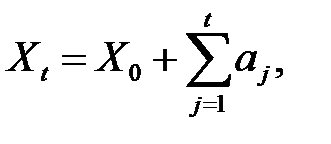 
где X 0 = х 0 - начальное значение процесса.
Отсюда получаем:
E (Xt | X 0 = х 0) = х 0,
D (Xt | X 0 = х 0) = D (a 1 +... + at) = D (a 1 ) +... + D (at) = t D (a 1) = t σ a 2.
Вследствие того, что дисперсия процесса (3.1) изменяется со временем, приходим к выводу, что модель СБ является нестационарным процессом.
Однако ряд (3.1) можно привести к стационарному виду, взяв первую разность, т.е. Δ Xt = Xt - Xt – 1 = (1 – В) Xt. При этом уравнение сведется к виду Δ Xt = at. Таким образом,модель (3.1) в первых разностях становится стационарной. График ряда первых разностей показан на рис.3.4.
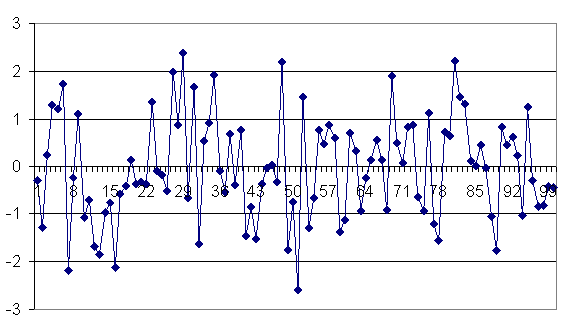
Рис.3.4. Ряд первых разностей
Такая операция взятия разностей может проводиться неоднократно, оценивая после каждой итерации ряд на стационарность. Применение такого подхода, т.е. взятия d последовательных разностей к нестационарным ВР с целью получения стационарных рядов вида ARMA было впервые описано в [2].
