Методы экспоненциального сглаживания (ЭС) часто рассматриваются как набор специальных методов для экстраполяции различных типов одномерных ВР. Большинство работ в области ЭС после 1980г. включало изучение эмпирических свойств этих методов, предложения по новым методам оценивания параметров, оценок прогноза и т.п. Появились многочисленные прикладные исследования по применению методов ЭС в компьютерной технологии, логистике, планировании производства. Предложенная в работе [7] таксономия обеспечила полезную кластеризацию для описания различных методов. Каждый метод состоит из одного из четырех видов тренда: нет тренда, аддитивный, мультипликативный, затухающий и одного из трех типов сезонности: нет сезонности, аддитивная, мультипликативная. В итоге имеем 12 различных методов, схематично представленных в табл.4.1.
Таблица 4.1 Кластеризация методов ЭС
| Трендовый компонент | Сезонный компонент | ||
| N (нет) | А (аддитивный) | М(мультипликативный) | |
| N (нет) | NN | NA | NM |
| А (аддитивный) | AN | AA | AM |
| М(мультипликативный) | MN | MA | MM |
| D(затухающий) | DN | DA | DM |
Методы ЭС представляет собой широкий класс процедур прогнозирования, которые основаны на простых уравнениях для вычисления прогноза и могут учитывать изменения локального уровня, тренда и сезонности. Рассмотрим вначале ситуацию, когда во ВР x 1, x 2,..., xN отсутствуют тренд и сезонность. Тогда прогнозное значение xN + 1 можно выразить взвешенной суммой прошлых наблюдений
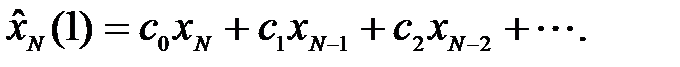(4.4)
где ci - весовые коэффициенты.
Представляется естественным придать большие веса последним наблюдениям, от которых в большей степени зависит величина xN + 1 , и меньшие веса наблюдениям, находящимся в начале ВР, т.е. далеко в прошлой истории ряда. Здесь более старым наблюдениям приписываются экспоненциально убывающие веса, при этом учитываются все предшествующие наблюдения ряда. Далее положим, что веса уменьшаются на постоянную величину при каждом единичном изменении временного лага. Для того чтобы сумма весов равнялась единице, примем
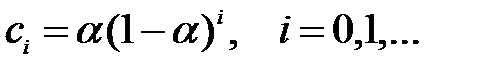
где α - параметр из диапазона 0 < α < 1.
Тогда уравнение (4.4) становится равным
(4.5)
Полученное уравнение (4.5) определяет простое экспоненциальное сглаживание (ПЭС), при котором вычисляется прогноз на один шаг вперед по формуле, эквивалентной геометрической сумме прошлых наблюдений. На практике выражение (4.5) может быть переписано в одной из двух эквивалентных формул:
· в виде рекуррентной формы
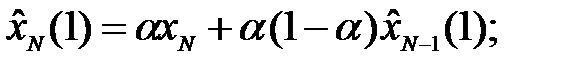(4.6)
· в виде коррекции ошибки
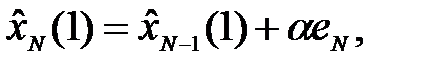(4.7)
где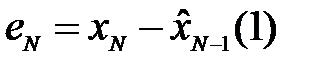 
- ошибка прогноза в момент времени N.
Хотя уравнения (4.6) и (4.7) выглядят различно, они дают идентичные результаты, поэтому их использование определяется практической необходимостью.
В работе [8] приведено обоснование метода ПЭС посредством применения модифицированного МНК к модели, состоящей из постоянного среднего значения μ и белого шума εt в виде
Xt = μ + εt.
Здесь величина μ оценивается с помощью геометрически спадающих взвешенных значений квадрата ошибки. Иными словами, параметр μ вычисляется путем минимизации выражения
где β j - весовые коэффициенты.
Описанная процедура ПЭС интуитивно понятна, но есть некоторые теоретические сомнения в постоянстве среднего значения μ, положенного в основу обычного МНК. Следовательно, при анализе нужно иметь в виду модель, в которой уровень только локально постоянен, но может меняться во времени. Считается, что метод ПЭС применяется для ВР, у которых отсутствуют сезонные компоненты или долговременный тренд, но имеется локально постоянное среднее значение, демонстрирующее некоторый «дрейф» (тенденцию) во времени. В действительности, можно показать [2], что метод ПЭС является оптимальным для ряда моделей, в которых форма дрейфа математически определена. Одной из таких моделей является модель ARIMA (0,1,1), описываемая уравнением
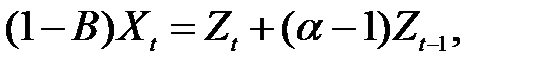(4.8)
в котором коэффициент помехи εt - 1 определяется как (α – 1) вместо обычно применяемого коэффициента θ. Это сделано для того, чтобы установить связь с параметром сглаживания α, используемым в методе ПЭС.
Тогда оптимальный одношаговый прогноз вперед, т.е условное среднее следующего наблюдения для выражения (4.8) определяется моделью ПЭС в виде (4.6) с параметром сглаживания α. Условие обратимости для модели ARIMA (0,1,1) приводит к ограничению 0< α < 2 на параметр сглаживания. Это шире, чем чем обычно используемый диапазон 0< α <1. В случае, когда α принимает знаечния из диапахона диапазона (1; 2), из формулы (4.5) следует, что веса, присваиваемые прошлым наблюдениям, при вычислении прогноза будут изменять свой знак.
Величина параметра сглаживания α зависит от свойств данного ВР. Значения α, лежащие между 0,1 и 0,3, используются чаще всего и формируют прогноз, который определяется большим числом прошлых наблюдений. Значения α, близкие к единице, применяются менее часто и дают прогноз, который в большей степени зависит от последних наблюдений. При α = 1 прогноз равен самому последнему наблюдению, и предыдущие наблюдения полностью игнорируются. Это видно и из выражения (4.8), которое при α = 1 сводится к модели простого случайного блуждания и дает для прогноза 
Если a = 0, то игнорируются текущие наблюдения.
Параметр α обычно ограничивается диапазоном (0...1) и часто оценивается минимизацией суммы квадратов ошибок прогноза по периоду подгонки ряда. Во многих программных пакетах описаны различные методы оценки этого параметра. На практике параметр сглаживания часто ищется с поиском на сетке. Возможные значения параметра разбиваются сеткой с определенным шагом. Например, рассматривается сетка значений от a = 0,1 до a = 0,9 с шагом 0,1. Затем выбирается то значение a, для которого сумма квадратов остатков является минимальной.
Отметим еще раз, что метод ПЭС не подходит для рядов, обладающих трендом и сезонностью, поэтому данный метод можно рассматривать как своего рода строительный блок для более общих версий экспоненциального сглаживания. Перед рассмотрением обобщающих закономерностей для методов ЭС полезно модифицировать ПЭС в части, относящейся к оценке локального уровня в момент времени t, которое обозначим как Lt. Выражение (4.6) при этом перепишется в виде
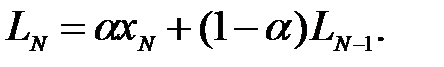(4.9)
Тогда одношаговый прогноз определяется как
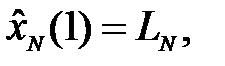(4.10)
и прогноз на h шагов вперед 
также будет равен LN.
Пример 4.2. Применим метод ПЭС к ряду, представляющему собой изменение числа авиапассажиров за 12 лет с помесячной регистрацией, так что длина ряда составляет 144 точки. Этот ряд ранее был представлен на рис.1.4.
Воспользуемся процедурой ПЭС для сглаживания ряда и прогноза на 12 месяцев вперед. Полученные результаты при ⍺ = 0,1 приведены на рис.4.5, где в дополнение к исходному и сглаженному рядам показан ряд остатков, а также прогноз на 12 месяцев вперед, который представляет собой прямую линию.
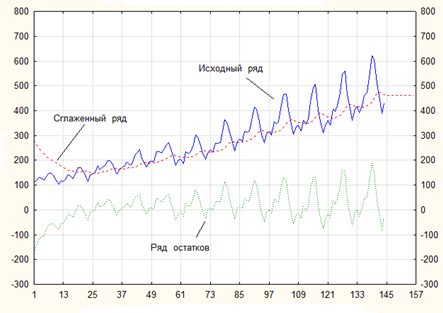
Рис.4.5 Исходный, сглаженный ряды и ряд остатков при ⍺ = 0,1
Вид графиков позволяет выявить два факта. Во-первых, сглаженный ряд имеет линейный тренд, но в нем имеются и сезонные колебания. Во-вторых, все значения прогнозов одинаковы. На самом деле это легко объяснить. Каждое сглаженное значение или прогноз L t вычисляется по формуле L t = L t- 1 + α *e, где e – ошибка, равная разности между наблюдаемыми и предсказанными (сглаженные или прогнозируемые) значениями. При вычислении прогнозов наблюдаемые значения отсутствуют, поэтому ошибка равна 0. Таким образом, все прогнозы одинаковые.
Результаты такой же операции, но при ⍺ = 0,9 показаны на рис.4.6.
Рис.4.6 Исходный, сглаженный ряды и ряд остатков при ⍺ = 0,9
Теперь сглаженные значения очень близки к наблюдаемым и отвечают ряду, сдвинутому на одно наблюдение вперед. В самом деле, при α = 1 каждое сглаженное наблюдение будет в точности равно предыдущему наблюдению, поэтому α можно назвать параметром жесткости. Чем меньше α, тем «жестче» сглаженный ряд и в нем меньше воздействий случайных флуктуаций. ■
Метод Хольта
Обобщим метод ПЭС до включения в модель коэффициента, определяющего локальный тренд, например, Tt, который характеризует увеличение или уменьшение уровня локального среднего за единичный временной период. Этот коэффициент также изменяется подобно уравнению для ЭС, но с другим параметром сглаживания γ. Модифицированное уравнение для локального уровня получается обобщением выражения (4.9) на случай наличия тренда, что в итоге дает
(4.11)
Кроме того, для локальной оценки тренда имеем следующее выражение
(4.12)
Прогноз на h шагов вперед получается очевидным образом
(4.13)
Уравнения (4.11), (4.12) соответствуют рекуррентной форме ЭС, которая выражается формулой (4.6).
Описанная процедура, приемлемая для ВР с локальным линейным трендом, называется методом Хольта для линейного тренда. Здесь имеются два параметра сглаживания ⍺ и γ, которые необходимо оценить.
Пример 4.3. Для того же ВР, что и в примере 4.2, выполним сглаживание и прогнозирование на 12 месяцев вперед.
На рис.4.7 показаны исходный, сглаженный ряды и ряд остатков при ⍺ = γ = 0,1. На этом же рисунке приведен прогноз, представляющий из себя прямую линию, т.е. сезонность в этом случае никак не учитывается. К тому же и степень сглаживания ряда очень высока: исходный и сглаженный ряды значительно различаются.
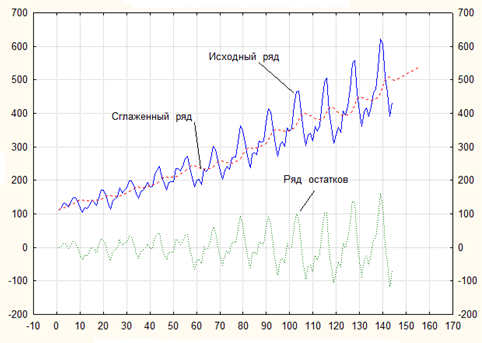
Рис.4.7 Исходный, сглаженный ряды и ряд остатков при ⍺ = γ = 0,1
Увеличим значения параметров сглаживания до величины 0,9, т.е. примем ⍺ = γ = 0,9. Полученные в этом случае результаты приведены на рис.4.8.
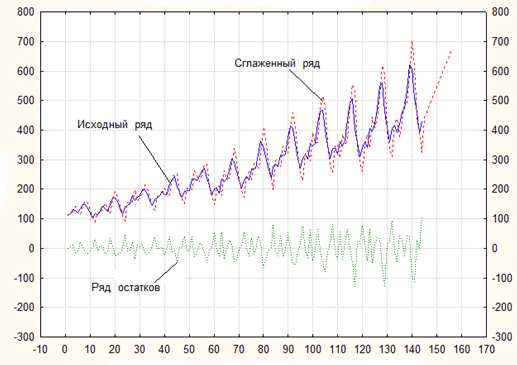
Рис.4.8 Исходный, сглаженный ряды и ряд остатков при ⍺ = γ = 0,9
На рис.4.8 сглаженные значения более похожи на наблюдаемые значения. Однако прогноз и этом случае также состоит из прямой линии, однако коэффициент наклона этой прямой больше, чем в первом случае при малых значениях параметров сглаживания. Таким образом, используя двухпараметрическую модель Хольта, можно «пропустить» значимое сезонное увеличение перевозок. ■
Метод Хольта – Винтерса
Экспоненциальное сглаживание далее может быть обобщено на случай сезонных вариаций. Пусть Lt, Tt, It определяют локальный уровень, тренд и сезонный индекс, соответственно, в момент времени t. Интерпретация индекса It зависит от того, какого рода сезонность: аддитивная или мультипликативная присутствует в рассматриваемом ВР. Напомним, что два вида сезонности описываются следующими выражениями:
· аддитивная
· мультипликативная
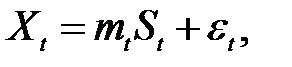
где mt - десезонный средний уровень (т.е. с устраненной сезонностью); St - сезонный эффект в момент времени t; ε t - случайная ошибка.
В первом случае xt - It есть десезонная величина; во втором - xt / It - десезонная величина. В аддитивной модели сезонные индексы ограничиваются так, что в сумме дают нуль по целому году. В мультипликативной - индексы должны усредняться до единицы. Значения трех величин Lt, Tt и It должны быть оценены по данному ряду, поэтому необходимо иметь три уравнения с тремя параметрами сглаживания ⍺, γ, δ. Как и прежде, эти параметры выбираются из диапазона (0...1).
Возьмем в качестве примера аддитивную модель, для которой рекуррентная форма уравнений для уровня LN, тренда TN и сезонного индекса IN имеет вид:
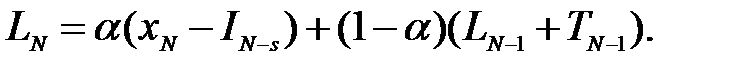
(4.14)
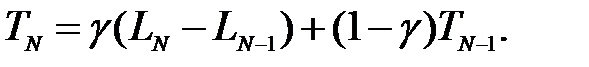(4.15)
(4.16)
Здесь s - число периодов в одном году (s = 4 для квартальных данных; s = 12 для месячных данных).
Прогнозы, начиная c момента времени N, определяются выражением
(4.17)
для h = 1, 2, …, s.
Для мультипликативной модели аналогичные уравнения имеют несколько отличный вид
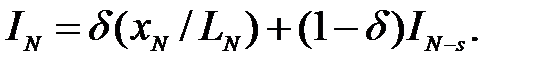
В этом случае прогнозы, начиная c момента времени N, определяются выражением
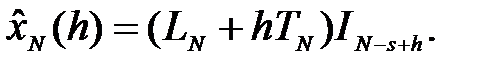(4.18)
Пример 4.4. Для того же ВР, что в примерах 4.2, 4.3 выполним сглаживание и прогнозирование методом Хольта-Винтерса.
На рис.4.9 показаны исходный, сглаженный ряды и ряд остатков при ⍺ = γ = δ = 0,1. Видно, что сглаженный ряд очень хорошо повторяет исходный, и на самом деле эффект сглаживания очень низок: два ряда практически одинаковы. Здесь же приведена оценка прогноза на 12 точек вперед, начиная с точки № = 145, откуда следует, что прогнозная кривая достаточно правдоподобно показывает грядущие значения ряда.
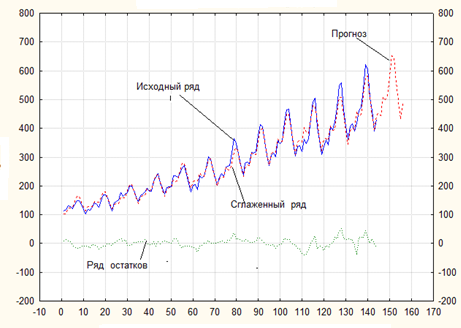
Рис.4.9 Исходный, сглаженный ряды и ряд остатков при ⍺ = γ = δ = 0,1
Результат аналогичных действий, но при при ⍺ = γ = δ = 0,9 показан на рис. 4.10.
Рис.4.10 Исходный, сглаженный ряды и ряд остатков при ⍺ = γ = δ = 0,9
Степень подобия кривой прогноза исходному ряду в этом случае меньше, чем в ситуации ⍺ = γ = δ = 0,1.
При опции "Автоматический поиск№ программа выполняет поиск лучшего набора параметров ⍺, γ, δ с помощью квази-ньютоновского алгоритма минимизации среднеквадратической ошибки. Результаты показаны на рис.4.11 и 4.12.
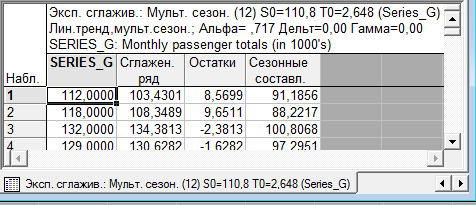
Рис.4.11 Результаты автоматического поиска
Как видно из рис.4.11, лучшее значение a для сглаживания остаточной случайной флуктуации равно 0,72, что позволяет сглаженным значениям следовать вблизи наблюдаемых данных. Кроме того, значения γ и δ близки к 0, т.е. модели имеют стабильный линейный тренд и сезонность.
Рис.4.12 Исходный, сглаженный ряды и ряд остатков при автоматическом поиске
Исходный и сглаженный ряды при автоматическом поиске почти сходны; прогноз в этом случае достаточно хорошо следует исходному ряду. ■
