Положим, что удалось идентифицировать конкретную модель для данного ВР, оценить параметры модели. Далее цель сводится к нахождению прогноза по подогнанной модели. Обозначим истинную модель индексом М и подогнанную модель - Mf. Из материала, изложенного в п.4.1, следует, что при использовании квадратичной функции потерь лучший способ вычисления прогноза заключается в выборе 
как условного МО величины XN + h по модели М и по доступной к моменту времени N информации IN. Таким образом, имеем
(4.19)
Для одномерного процесса информация IN состоит из значений ряда xN, xN – 1,... и текущего значения времени N. На практике гораздо чаще используется подогнанная модель Mf, чем истинная.
В главе 2 было показано, что стационарный ВР может быть представлен с помощью теоремы Вольда (2.19) как процесс, состоящий из бесконечного числа слагаемых
(2.19)
где ψ0 = 1; 
{ at } – чисто случайный процесс с нулевым средним и постоянной дисперсией σ2.
Последовательность случайных величин, удовлетворяющих уравнению (2.19), называется обобщенным линейным процессом. Прогнозное значение XN + h с минимальной СКО для этого процесса определяется как [1]
(4.20)
При выводе формулы (4.20) были сделаны следующие допущения:
· значения ψ j - известны;
· исторические данные ряда до момента времени N, т.е. { xt, t ≤ N } - известны.
При этих допущениях могут быть найдены значения { at, t ≤ N }, обозначенные как { at }. Уравнение (4.20) является очевидным, так как оно следует из выражения (2.19) при замене будущих значений at нулем, настоящих и прошлых значений at - их наблюдаемыми величинами.
Определим с учетом последних замечаний прогнозные оценки для различных моделей временных рядов. Укажем еще раз, что последний отсчет ряда сделан при значении аргумента, равного N; прогнозные оценки вперед отсчитываются от этой величины. Такие оценки могут быть получены не только с помощью уравнения (4.20), но и вычислены непосредственно из уравнений, которыми описываются ВР, заменой: 1) будущих значений at нулем; 2) будущих значений Xt их условным математическим ожиданием; 3) настоящих и прошлых значений Xt и at их наблюдаемыми значениями.
Рассмотрим несколько примеров вычисления прогнозов.
Пример 4.5. Модель AR (1): Xt = ф 1 Xt - 1 + at
Прогноз на один шаг вперед:
x ( h =1)-1 - это значение определяется последним наблюдением, следовательно, x ( h = 1)-1 = xN;
ah = 1 = 0 как будущее значение помехи.
Прогноз определяется как
(4.21)
Прогноз на два шага вперед:
x ( h =2)-1 = xh =1; последнее значение неизвестно, есть только прогноз в этой точке, следовательно: x ( h =2)-1 = xh =1= 
.
ah = 2 = 0 как будущее значение помехи.
Прогноз определяется как
(4.22)
Прогноз на l шагов вперед, основанный на минимуме СКО, есть условное математическое ожидание величины xN + l, равное
(4.23)
где 
если i < 0.
Можно показать, что для стационарной модели AR (p) величина 
сходится к E (Xt) при l → ∞. Последнее означает, что для такого ряда долговременный прогноз стремится к безусловному среднему. ■
Пример 4.6. Модель МА (1): Xt = at + θ1 а t – 1
Прогноз на один шаг вперед:
С учетом условного МО величины 
и того факта, что
ah = 1 = 0 как будущее значение помехи; a ( h = 1) -1 = aN,
для прогноза получим
. (4.24)
Прогноз на два шага вперед:
Учитывая соотношения: ah = 2 = 0; a ( h = 2)-1 = ah = 1 = 0, для прогноза получим
. (4.25)
Итоговый результат - очевиден, так как для модели МА (1) прогноз обрывается при значениях h ≥ q.
Прогноз на l шагов вперед:
В общем случае 
для l ≥ 2. Таким образом, многошаговый прогноз для модели МА (1) стремится к безусловному среднему этого процесса. График прогноза этой модели образует прямую линию после первого шага. ■
Пример 4.7. Модель AR МА (1,1): Xt = ф 1 Xt - 1 + at + θ1 а t – 1
Прогноз на один шаг вперед:
С учетом условного МО величины и того факта, что
x (h = 1)-1 = xN; ah= 1 = 0; a (h= 1)-1 = aN,
для прогноза получим
(4.26)
Прогноз на два шага вперед:
x ( h =2)-1 = xh =1= ; ah = 2 = 0; a ( h = 2) -1 =0,
для прогноза получим
(4.27)
Прогноз на l шагов вперед проводится аналогичным образом, учитывая, что
если l – i ≤ 0;
aN (l – i) > 0, если l – i > 0;
aN (l – i) = ah+l –i, если l – i ≤ 0. ■
Необходимо сделать следующее замечание по поводу параметров моделей. На практике эти параметры точно неизвестны и должны быть оценены по имеющимся данным. Кроме того, в нашем распоряжении нет бесконечного числа доступных прошлых наблюдений, как это требуется при использовании формулы (4.20). В действительности, вместо, например, формулы (4.26), применяется ее рабочая версия, имеющая вид
, (4.28)
где вместо параметров модели стоят оценки параметров, найденные из наблюдаемых данных.
Использование оценок увеличивает ошибку прогнозирования, и это объясняет различие между применением истинной М и подогнанной моделей М f.
Полученные результаты прогнозирования для стационарных ВР могут быть распространены для нестационарных ВР класса ARIMA (p, d, q).
Пример 4.8. Модель ARI МА (1,1,1): Xt = ф 1 (1 - B) Xt - 1 + at + θ1 а t – 1.
Формулу для модели ARI МА (1,1,1) можно переписать в следующем виде
Xt = (1 + ф 1) Xt - 1 - ф 1 Xt - 1 + at + θ1 а t – 1.
Прогноз на один шаг вперед:
x (h = 1)-1 = xN; x (h = 1)-2 = xN- 1; ah= 1 = 0; a (h= 1)-1 = aN.
Итоговая формула для прогноза в этом случае имеет вид
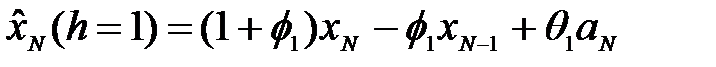. (4.29)
Прогноз на два шага вперед:
x (h =2)-1 = xh =1= ; x (h =2)-2 =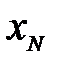 
; ah= 2 = 0; a (h= 2)-1 = 0.
Итоговая формула в этом случае запишется как
(4.30)
Аналогичным образом осуществляется прогноз на l шагов вперед. ■
Представляет интерес построение прогнозных оценок для модели для ARI МА (0,1,1), которую можно записать как
Xt = Xt - 1 + at + θ1 а t – 1.
Прогноз на один шаг вперед:
x (h = 1)-1 = xN; ah= 1 = 0; a (h= 1)-1 = aN.
Итоговая формула для прогноза в этом случае имеет вид
(4.31)
Выражение (4.31) после некоторых алгебраических преобразований становится равным
(4.32)
где 
Полученная формула (4.32) совпадает с ранее выведенным соотношением (4.6), которое применяется при простом ЭС, и таким образом существует явная связь между различными способами построения прогнозных оценок.
Литература
1. Chatfield C. Time-series forecasting. Chapman & Hall/CRC, London, 2000. - 266р.
2. Chatfield C. The Analysis of Time Series—An Introduction. Chapman & Hall/CRC, London, 2005. - 358р.
3. Vapnik V. N. Statistical Learning Theory. N. Y.: Wiley.1998. - 626 р.
4. КолмогоровА.Н.Интерполирование и экстраполирование стационарных случайных последовательностей. Изв. АН СССР, серия математическая, 1941, т. 5, № 1, с. 3-14.
5. Wiener N. Extrapolation, interpolation and smoothing of stationary time series, N. Y., 2013 (Reprint of 1949 Edition). -174р.
6. Hilborn R.C. Chaos and Nonlinear Dynamics. - New-York, Oxford University Press, 2000. - 650р.
7. Hyndman R. J., Koehler A. B., Snyder R. D. & Grose S. A state space framework for automatic forecasting using exponential smoothing methods. International Journal of Forecasting, 2002,18, 439–454.
8. Brown, R. G. Smoothing, forecasting and prediction of discrete time series. Englewood Cliffs, NJ7 Prentice-Hall.1963. - 468р.
[1] Показатель Ляпунова представляет собой меру скорости расхождения траекторий, начинающихся в соседних точках.
