Для долговременного прогнозирования несезонных данных полезно использовать трендовые кривые, построенные для последовательных значений ряда, и их дальнейшей экстраполяции. Такой подход обычно применяется для годичных данных, из которых уже убрана сезонность, и, следовательно, ряды являются очищенными от вариаций, вызванных этой причиной. В п.1.6.1 были проанализированы различные виды тренда, включая квадратичный, логистический и др., поэтому, не останавливаясь вновь на этих определениях, укажем дальнейшие шаги построения прогноза. В первую очередь, нас интересует горизонт прогноза. К сожалению, дать простой ответ на этот вопрос не представляется возможным, так как аналитического выражения для определения такого горизонта нет. Лишь в одном случае, а именно, при хаотическом ВР можно найти горизонт аналитическим путем: здесь искомый параметр определяется величиной, равной обратному значению наибольшего показателя Ляпунова.[1] Отметим, что выдающийся русский математик А.М.Ляпунов являлся одним из основоположников современной теории хаоса [6]
В нашем же случае для определения горизонта прогноза существуют различные мнемонические правила. Например, рекомендуется на десять точек доступных наблюдений дать одну точку прогноза. В [1] указывается, что нецелесообразно делать прогнозы на горизонт больший, чем половина точек, для которых имеются доступные данные. Разумеется, имеющаяся модель тренда позволяет при увеличении аргумента (времени) получить оценку прогноза на достаточно большом горизонте, однако достоверность такого точечного прогноза будет крайне низкой.
Пример 4.1. Воспользуемся смоделированным рядом длиной 50 наблюдений, который представляет собой сумму линейного тренда и шумовой помехи с нулевым средним и СКО = 5. График ряда показан на рис.4.2. В качестве оценки прогноза проведем экстраполяцию ВР.

Рис.4.2 Смоделированный временной ряд
Для этого ВР подберем аналитическое выражение в виде линейной функции y = (1,08 + 1,97* x) и проведем экстраполяцию на 10 точек вперед. На рис.4.3 приведены результаты такой прогнозной оценки, которая начинается из точки с номером 51 и простирается до точки с номером 60. Видно, что модель достаточно хорошо описывает исходные данные: рассчитанный коэффициент детерминации составляет величину, равную 0,97.

Рис.4.3 Подобранная линейная модель и ее экстраполяция
Кроме того, остатки, т.е. разности между предсказанными и наблюдаемыми значениями распределены примерно по нормальному закону, что подтверждается графиком на рис.4.4. ■
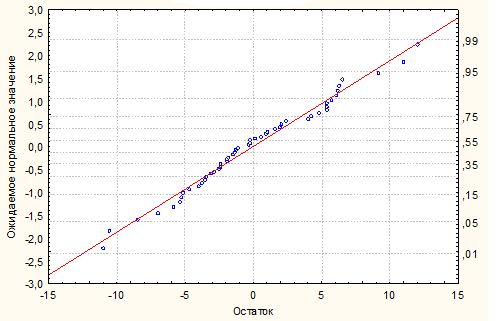
Рис.4.4. Распределение остатков
Недостаток применения трендовых кривых для прогнозирования заключается в том, что отсутствует логическая основа выбора линий тренда. На практике часто встречаются ситуации, когда можно подобрать несколько кривых, описывающих наблюдаемый ряд, но при прогнозе различные модели дают, разумеется, разные оценки прогноза.






