Глава 4 Прогнозирование одномерных временных рядов
4.1 Задача прогнозирования временных рядов. 1
4.2 Экстраполяция трендовых кривых. 9
4.3 Простое экспоненциальное сглаживание. 12
4.4 Метод Хольта. 18
4.5 Метод Хольта – Винтерса. 21
4.6 Прогнозирование на основе моделей. 25
Прогнозирование будущих значений наблюдаемых ВР представляет собой важную проблему во многих областях, включая экономику, планирование производства, объем продаж и т.п. В данной главе основное внимание уделяется нахождению будущих значений одномерных рядов. Положим, что имеется единственный наблюдаемый ВР, обозначенный как x 1, x 2,.. ., xN, и необходимо спрогнозировать значения ряда xN + h для h = 1, 2, …. Параметр h обычно называется горизонтом прогноза. Сущность метода прогноза одномерного ВР сводится к вычислению точечного прогноза 
, основанного на прошлых и настоящей величинах данного ряда. Одномерные методы применяются в ситуациях, когда имеется большое число рядов для предсказания, опыт аналитика недостаточен или для многомерных рядов требуются прогнозы объясняющих переменных. На выбор конкретного метода оказывают влияние цели анализа, доступные данные, качество данных, имеющееся в распоряжении программное оборудование и т.п. Вначале обсуждается проблема "лучшего" прогноза для ВР, далее рассматривается использование трендовых кривых для построения прогноза и применение методов экспоненциального сглаживания. Завершается глава формированием прогнозных оценок на основе уже рассмотренных моделей.
Задача прогнозирования временных рядов
Прогнозы представляют собой условные утверждения о будущем поведении, основанные на определенных допущениях. Таким образом, предсказанные характеристики не являются раз и навсегда установленными, и аналитик должен быть готов к изменению прогнозов при получении любой дополнительной информации.
Укажем вначале возможные методы прогнозирования, хотя какой-либо общепринятой классификации этих методов не существует, и различные авторы придерживаются разных точек зрения по этому поводу. В дальнейшем будем ориентироваться в этом вопросе на работы известного английского ученого К.Чатфилда [1,2], который разбивает совокупность методов на три группы:
1 .Субъективные
Прогнозы могут быть сделаны на субъективной основе, используя суждения, интуицию и любую другую доступную информацию. Подходы этой группы простираются от одиночных высказываний до метода Дельфи, сущность которого заключается в том, что с помощью последовательных действий группа экспертов добивается консенсуса при определении правильного решения. Здесь такие методы не описываются, так как аналитики хотят получить прогноз, который, хотя бы частично, являлся объективным. Однако отметим, что некоторые субъективные суждения применяются в ряде статистических процедур, например, при выборе подходящей модели.
2. Одномерные
Для одномерного ряда, простирающегося до значения N, обозначим прогноз на h шагов вперед как 
. Последняя величина может включать функцию времени, например, детерминированный линейный тренд, но в нашей задаче сконцентрируем внимание на более общем случае, когда прогнозное значение выражается как некоторая функция наблюдаемых данных xN, xN - 1, xN - 2,..., в частности, 
Сразу же возникает несколько вопросов относительно функции g:
1. Что выбрать в качестве функции g?
2. Какими свойствами должна обладать эта функция?
3. Дает ли эта функция "лучший" прогноз?
4. Что означает термин "лучший" прогноз?
Прогнозные значения основаны на модели, подогнанной только для настоящего и прошлых наблюдений данного ряда. Это означает, что одномерные прогнозы, к примеру, будущих продаж какого-то продукта принимают во внимание только прошлые продажи и не учитывают другие экономические факторы. Приемы, включаемые в эту группу, иногда называют наивными или проекционными методами.
3. Многомерные
Прогноз конкретной переменной зависит, по крайней мере, от значений одного или более дополнительных рядов, называемых предикторами или объясняющими переменными. Например, прогноз продаж может зависеть от времени года, экономических индексов, цены акций. Модели этого типа иногда называют каузальными.
На практике процедура прогнозирования может включать комбинацию таких приемов. В частности, маркетинговые прогнозы обычно учитывают агрегирование статистических предикторов с субъективными оценками рынка. Более формализованная оценка прогноза может быть получена вычислением взвешенного усреднения двух или больше объективных прогнозов.
Выбор метода прогнозирования зависит от различных факторов, которые необходимо принимать во внимание:
· тип ВР и его свойства (наличие тренда и сезонности);
· доступность прошлых наблюдений;
· цель использования прогноза;
· длину горизонта прогнозирования;
· навык и опыт аналитика.
В начале процедуры прогнозирования нужно рассмотреть вопрос об оценке прогнозных значений, т.е. необходимо выбрать приемлемую функцию потерь (ФП). Последнюю можно определить следующим образом: пусть e обозначает ошибку прогнозирования, равную
(4.1)
где 
- наблюдаемое значение;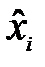 
- прогнозное значение.
Тогда ФП L (e) определяет потери, связанные с величиной ошибки прогнозирования e. Обычно ФП обладает рядом типичных свойств:
1. L (0) = 0.
2. L (e) - непрерывная функция, которая возрастает при увеличении абсолютного значения e.
3. L (e) = L (- e), т.е. ФП является симметричной (однако встречаются и несимметричные ФП).
На рис.4.1 приведены четыре возможных вида ФП.
Рис.4.1 Виды функций потерь (а - квадратичная; б - Лапласа; в - Хубера; г - ε-нечувствительная)
ФП, показанная на рис.4.1.а, соответствует часто используемой квадратичной зависимости потерь, которая описывается выражением
В ряде ситуаций лучшее приближение к регрессии дают оценки, основанные на лапласовых ФП (рис.4.1.б), в частности,
На рис.4.1.в приведена ФП, которую предложил П.Хубер в 1964 г. Его ФП имеет квадратичную зависимость от ошибки вблизи нуля и линейную зависимость на некотором удалении от нуля. Аналитически такая ФП имеет вид:
где k - заранее установленная величина.
На рис.4.1.г показана так называемая ε-нечувствительная ФП, введенная В.И.Вапником [3] в разработанном им методе опорных векторов, которая выражается как
где ε - величина, определяющая зону нечувствительности.
ФП, описываемая последним выражением, характеризует потери следующим образом: потери равны нулю, если разность между предсказанным и наблюдаемым значениями меньше, чем ε.
"Хорошее" предсказание может быть определено как прогноз, который минимизирует средние потери по плотности вероятности ошибок прогнозирования. На практике достаточно трудно выявить приемлемую ФП, поэтому чаще других используется квадратичная ФП.
Наряду с ФП при выполнении прогнозирования ВР представляет значительный интерес мера точности прогноза. Самой простейшей и наряду с этим наиболее часто применяемой мерой является средний квадрат ошибки (mean square error - MSE), равный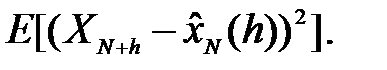 
Фактически можно показать, что эта мера точности включает квадратичную ФП. В этом случае "лучший" прогноз в смысле минимизации MSE представляет собой условное ожидание величины XN + h, найденное через наблюдения, которые доступны к моменту времени N, т.е.
(4.2)
Для оценки общего выражения для условного ожидания будущего значения, т.е. 
, необходимо знать полное условное распределение величины XN + h, что является целью так называемого прогнозирования плотности (density forecasting). В качестве альтернативы достаточно определить совместное распределение вероятностей величин { XN + h, XN, XN -1, ... }. Обычно это возможно только для некоторых моделей, например, для линейных моделей с нормальными ошибками. Отчасти по этой причине большая часть материалов по общей теории прогнозирования ограничивается рассмотрением линейных предикторов следующей формы
(4.3)
где проблема сводится к нахождению подходящих весов { wi }, которые минимизируют ошибку прогноза MSE. Полученные таким образом результаты иногда называют прогнозами, найденными посредством линейного МНК. В ситуации, когда процесс является совместно гауссовым, можно показать, что линейный предиктор действительно минимизирует ошибку прогноза MSE. Даже если процесс не является гауссовым, линейный предиктор может обеспечить хорошее приближение к наилучшему прогнозу с минимальной ошибкой прогноза MSE.
Необходимо отметить, что основополагающие результаты в области предсказания были получены известным российским ученым А.Н. Колмогоровым еще в 1941 г., когда он опубликовал работу [4] с математическими основами теории прогнозирования. Аналогичные результаты были получены американским ученым Н.Винером во время Второй мировой войны, однако вследствие военного применения только в 1949 г. закрытый отчет с этими данными был рассекречен и опубликован как монография [5]. Позже эти результаты получили название теории Винера-Колмогорова.
В соответствии с этой теорией при прогнозировании необходимо знать истинную корреляционную функцию процесса (или, что эквивалентно, спектра). В этом случае можно получить прогнозную оценку, основываясь на линейном МНК. Кроме того, требуется бесконечная сумма наблюдаемых прошлых данных. Ни одно из этих условий не удовлетворяется на практике, и обычно достичь положительного результата удается лишь в том случае, если оцениваемый спектр можно представить в виде рациональной функции. Например, в ситуации, когда исследуемый процесс описывается моделью ARMA, легче получить прогнозную оценку с использованием этой модели, чем с применением результатов линейного предсказания теории Винера-Колмогорова. Подход, развиваемый в указанной теории, может рассматриваться как непараметрический вследствие того, что он базируется на знании корреляционной функции или спектра, а не на подогнанной модели.
