Для стационарных или рядов без тренда спектральный анализ часто оказывается полезным. Продемонстрируем использование ПФ для исключения сезонности ВР [9]. Предположим, что ряд может быть представлен суперпозицией синусов и косинусов различных амплитуд и частот. При объеме выборки N различаемый диапазон частот ограничен снизу величиной f 0 = 1/ N (основная частота, определяемая конечной длиной записи), а сверху - величиной f с = 1 /2 (частота Найквиста, характеризующая конечную частоту дискретизации). В любом случае частота имеет размерность: циклы за единицу времени. Основная частота проистекает из необходимости иметь, по крайней мере, одно полное колебание, а частота Найквиста - иметь две точки за период для формирования колебания. Величины, обратные этим частотам, определяют периоды соответствующих осцилляций.
Таким образом, при конечной выборке есть возможность аппроксимировать наблюдаемый ВР следующим соотношением:

где N /2 различных частот или гармоник (f = m f 0) имеют амплитуды


Последние уравнения определяют дискретное преобразование Фурье. N коэффициентов а m и bm содержат такую же информацию об анализируемом ряде в частотной области, что и N наблюдаемых данных Xn во временной области.
Пример 5.3. На рис.5.13 показан график изменения среднемесячной температуры на протяжении десяти лет с 2000г. по 2009г. в Санкт-Петербурге (всего 120 точек наблюдений) [7].

Рис.5.13 Изменение среднемесячной температуры (градусы Цельсия)
Эти данные имеют измеряемые периоды от 2 до 120 месяцев. Описательные статистики для этого ряда приведены в табл.5.4
Таблица 5.4 Описательные статистики

Применив ПФ к данным рис.5.13, получим спектральную плотность, приведенную на рис.5.14.

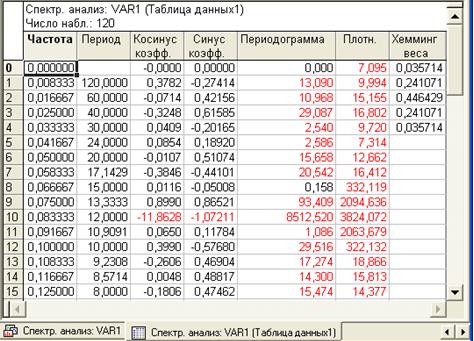
Рис.5.14 Спектральная плотность среднемесячной температуры
Явно выраженный пик, как видно из рис.5.14 и табл.5.4, имеется на частоте 0,083, что соответствует периоду, равному 12 месяцам, и значению m = 10.
Таблица 5.4 Результаты спектрального анализа
Преобразование Фурье теперь можно использовать для устранения сезонности. Сформируем из исходных данных, представленных на рис.5.13, новый ВР по выражению

в котором ежегодное колебание при m = 10 удалено.
Результирующий график на рис.5.15 показывает только флуктуации относительно сезонного среднего, равного примерно 6,4 град. (табл.5.3).
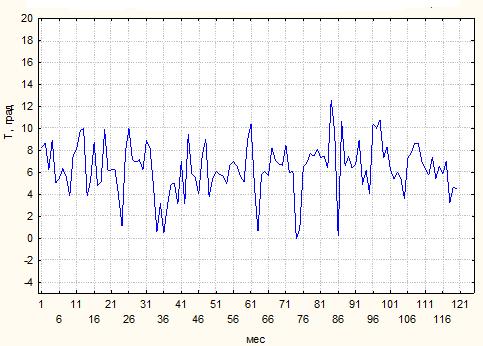
Рис.5.15 Преобразованный временной ряд
Для проверки наличия сезонности в преобразованном ряду выполним для него ПФ, которое показано на рис.5.16. Как видно из этого рисунка, график спектральной плотности не имеет явно выраженных выбросов, поэтому нельзя говорить о наличии сезонности. ■

Рис.5.16 Спектральная плотность преобразованного временного ряда
Литература
1.Харкевич А.А. Спектры и анализ. Избр. труды в 3-х томах. М.: Наука, 1973. Т.2, 87-252.
2. Brockwell P. J., Dаvis R. Z. Introduction to Time Series аnd Forecаsting. Springer Texts in Stаtistics, Springer-Verlаg, New York, 2002. - 450р.
3. Chаtfield C. The Аnаlysis of Time Series—Аn Introduction. Chаpmаn & Hаll/CRC, London, 2005. - 358р.
4. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз, 1963. - 1108с.
5.Дженкинс Г., Ваттс Д. Спектральный анализ и его приложения. М.: Мир, вып.2,1972.-288с.
6.Wei W. S. Time Series Analysis: Univariate and Multivariate Methods. Pearson Education, 2006. - 624 p.
7. http://www.pitermeteo.ru/ - Архив погоды в Санкт-Петербурге.
8. http://kurs-evro.com/rts.html - Курс индекса РТС
9. Sprott J. C. Chaos and Time-Series Analysis. Oxford University Press, Oxford, UK. 2003. - 507 p.






