Рассмотрим ВР, который содержит детерминированный синусоидальный компонент на частоте ω и случайную помеху. Модель такого ряда имеет вид
(5.28)
где Zt - случайный процесс; μ, α, β – параметры, оцениваемые по данным.
Обозначим наблюдения, взятые через единичный интервал времени, как x 1, x 2,..., xN. Отметим, что необходимые алгебраические преобразования значительно упростятся, если ограничиться рассмотрением случая четного N. В противном случае (N - нечетное) рекомендуется отбросить несколько первых наблюдений (программные продукты отбрасывают первое наблюдение), чтобы сделать N четным. При достаточно большом N потеря информации незначительна.
Для модели (5.28) математическое ожидание может быть выражено через матричное обозначение следующим образом
где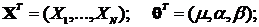 
.
Так как эта модель линейна по параметрам μ, α, β, она является общей линейной моделью. В этом случае с использованием метода наименьших квадратов для оценок θ получим
(5.29)
Приведенная формула, известная из регрессионного анализа, применима для любых значений частоты ω, но практический смысл имеют те частоты, которые не являются достаточно высокими или низкими. Наивысшая частота, удовлетворяющая данным, есть частота Найквиста, равная π, которая формирует один цикл каждые два наблюдения. Рассмотрим более подробно частоту Найквиста.
Дадим более развернутое описание этой частоты. Если наблюдения взяты через равные интервалы времени длиной Δ t, тогда угловая частота Найквиста определяется как ω N = π / Δ t. Соответствующая частота, выраженная в циклах на единицу времени, составит величину 
Рассмотрим следующий пример. Положим, что показания температуры воздуха в некотором городе регистрируются в полдень. Ясно, что эти наблюдения ничего не говорят нам об изменениях температуры в течение дня. С единственным наблюдением за день частота Найквиста определяется как ω N = π радиан в день (или один цикл за два дня). Это ниже, чем частоты, которые соответствуют изменениям в течение дня. Например, вариации за один день имеют угловую частоту ω = 2π радиан в день или f = 1 цикл в день. Для получения информации об изменениях в течение дня на этих, более высоких частотах, необходимо увеличить частоту выборки и взять два или больше наблюдений в день. Те же выводы справедливы и в примере с годичными данными продаж. Очевидно, они не дадут информации о любых сезонных эффектах, в то время как месячные или квартальные наблюдения позволят определить наличие сезонности.
На другом конце спектра находится самая низкая частота, которая совершает один цикл на всей длине ВР. Приравнивая цикл длиной 2π / ω количеству наблюдений N, находим значение наинизшей частоты, равное 2π / N. Объясним теперь, почему ниже этой частоты не имеет смысла пытаться подгонять данные. При наличии наблюдений температуры только за 6 месяцев с зимы до лета аналитик не в состоянии решить, имеется ли растущий тренд в данных или в самом ли деле зимой холоднее, чем летом. Однако с годичными данными эта задача решается легко. Таким образом, если мы интересуемся изменениями на низкой частоте (один цикл за год), необходимо иметь, по крайней мере, данные за один год. При недельных данных за один год имеем: N = 52,
Δ t = 1 неделя, и наинизшая угловая частота 2π/ N Δ t соответствует частоте 1/ N Δ t циклов за неделю. Самая низкая частота здесь составляет величину 1/52 в неделю, которая теперь может быть преобразована в один цикл за год. Наинизшая частота 2π/ N Δ иногда называется фундаментальной (основной) частотой Фурье, так как представление данных в ряд Фурье обычно оценивается на частотах ω p = 2π p / N Δ для
p = 1, 2,…, N / 2, которые называются гармониками.
Формула (5.29) для оценок 
упрощается, если ω ограничить одним из значений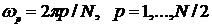 
, которые находятся на равных расстояниях от самой низшей частоты 2π/ N до частоты Найквиста π. В этом случае член 
в формуле (5.29) становится диагональной матрицей, учитывая хорошо известные тригонометрические результаты:
Суммирование во всех формулах (5.30) проводится по t от 1 до N. При диагональной матрице легко получить оценки , так как обратная матрица 
является также диагональной. Для ω p такой, что p ≠ N /2, можно найти [ 3]:
(5.31)
В случае, когда p = N /2, оценка для β становится равной нулю для всех t, что приводит к такому итоговому результату
Первоначальные попытки раскрыть "спрятанные" периодичности в рассматриваемом ВР сводились к проведению анализа, аналогичного вышеприведенному для всех частот 2π/ N, 4π/ N,..., π.Учитывая выражения (5.30) и ортогональность различных членов, в конечном итоге приходим к следующему выражению для xt в виде ряда Фурье
(5.32)
для t = 1, 2, …, N.
В выражении (5.32) коэффициенты ряда имеют вид
(5.33)
Анализ с использованием формул (5.32),(5.33) иногда называется анализом Фурье или гармоническим анализом. Стоит отметить, что коэффициенты в формулах (5.33) на данной частоте ω являются такими же, как оценки коэффициентов модели (5.28), полученные МНК.
Общий эффект анализа Фурье, примененного к данным, заключается в разделении дисперсии ряда на составляющие на частотах 2π/ N, 4π/ N,..., π. Компонент на частоте ω p = 2π p / N называется р -ой гармоникой.
Для p ≠ N /2 может оказаться полезным записать р -ую гармонику в следующей эквивалентной форме
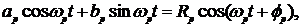(5.34)
где 
- амплитуда р -ой гармоники; 
- ее фаза.
Можно показать, что для p ≠ N /2 вклад р -ой гармоники в общую сумму квадратов определяется как 
. Это выражение через амплитуда р -ой гармоники определяется как 
. С использованием формул (5.30), (5.32) после некоторых алгебраических преобразований получим
.
Разделив полученное выражение на N, имеем
(5.35)
Формула (5.35) представляет собой запись теоремы Парсеваля. Левая часть этого выражения определяет дисперсию наблюдений. Таким образом, 
является вкладом р -ой гармоники в дисперсию.
При построении графика в функции от ω p = 2π p / N получим линейный спектр. Различные типы такого спектра имеют место, например, в физике, при прохождении света в газоразрядной лампе и наблюдении его с помощью спектроскопа. Свет обладает энергией на дискретных частотах, и его энергия изображается в виде ярких полос.
Если считать как вклад в дисперсию в диапазоне ω p ± π / N, то можно построить гистограмму, высота которой в этом диапазоне является такой, что
= площади прямоугольника гистограммы = высота гистограммы, умноженная на 2π / N.
Таким образом, высота гистограммы на частоте ω p, обозначенная как I (ω p), есть
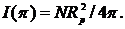(5.36)
Как обычно, уравнение (5.36) неприменимо для p = N /2, поэтому величину 
можно считать как вклад в дисперсию в интервале [(N - 1) π/ N, π], так что
График I (ω) в зависимости от ω называется периодограммой, хотя чаще I (ω) является функцией частоты, чем периода. Отметим, что формула для и, следовательно, для I (ω) может быть записана несколькими эквивалентными способами, которые имеют различный вид. Например, после ряда алгебраических выкладок можно показать, что
(5.37)
Непосредственный способ вычисления периодограммы по данным наблюдений заключается в использовании выражения
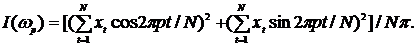(5.38)
Формула (5.38) справедлива и для p = N /2.
Другие авторы определяют периодограмму иным образом, чем записано в выражении (5.37), но разница обычно возникает из-за наличия отрицательных частот или использования циклической частоты f = ω /2π вместо ω [5,6].
Пример 5.1. На рис.5.5 приведен график ежедневной температуры в СПб за 3 года (2010-2012 гг.), всего 3*365 = 1095 наблюдений [7].
Рассчитанные периодограммы этого ВР в функции частоты и периода показаны на рис.5.6.а, 5.6.б, соответственно.
Рис.5.5 Изменение ежедневной температуры в СПб за 3 года
а)
б)
Рис.5.5 Периодограмма ряда изменения температуры
В табл.5.1 приведены рассчитанные значения периодограммы.
Таблица 5.1 Результаты спектрального анализа
Оценивание спектра в виде периодограммы является очевидным способом формирования оценки, но она обладает недостатками в части состоятельности оценок, поэтому требуются некоторые модификации метода оценивания.
Сглаживание спектра
Вначале рассмотрим оценки спектра ряда, который выражается через автоковариации так, как указано в уравнении (5.20):
Последнее равенство перепишем следующим образом
(5.39)
Основываясь на данных наблюдений ВР, при оценивании f (ω) заменим теоретические автоковариации γ h их выборочными значениями 
. Однако для ВР, состоящего из N точек, можно вычислить только для h = 0, 1,..., (N – 1). Следовательно, для оценки спектра получим
(5.40)
Последнее выражение определяет выборочный спектр. Так как величины являются асимптотически несмещенными, имеем
(5.41)
Таким образом, оценка спектра 
является несмещенной. Можно показать [6,p.300], что, несмотря на несмещенность оценки выборочного спектра в виде (5.40), ее дисперсия не стремится к нулю при увеличении N, поэтому не удовлетворяет условию состоятельности оценки.
При увеличении длины ряда и уменьшении интервала между соседними частотами ω h и ω j ковариация 
будет стремиться к нулю. В результате этого оценка становится нестабильной и принимает очень изрезанный вид, как это показано на рис.5.6. Представленные графики остаются такими же нестабильными, несмотря на увеличение размера выборки. Для устранения таких нежелательных свойств необходимо перейти к сглаживанию периодограмм и выборочных спектров.
а)
б)
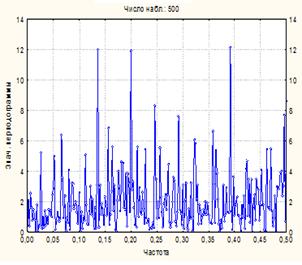
в)
Рис.5.6 Временные ряды (белый шум) - слева; соответствующие периодограммы - справа; (а – 100 точек; б - 200 точек; в - 500 точек)
Естественный путь снижения дисперсии выборочного спектра заключается в его сглаживании в области, прилегающей к рассматриваемой частоте. Иными словами, спектральная оценка представляет собой сглаженный спектр, полученный путем взвешенного усреднения m значений слева и справа от частоты ω k, т.е.
(5.42)
где ω k = 2π k / N; k = 0, ±1,..., ± N /2 - частоты Фурье; mN указывает на то, что m является функцией N; WN (ω j) - весовая функция, обладающая следующими свойствами:
(5.43)
Весовая функция WN (ω j) называется спектральным окном, потому что только некоторые из спектральных ординат используются в сглаживающей сумме. Если спектр f (ω) является плоским и приблизительно постоянным в пределах окна, тогда имеем
(5.44)
Из свойства (5.43): 
следует, что дисперсия сглаженного спектра уменьшается при увеличении m. Величина m определяет число частот, участвующих в сглаживании. Этот параметр непосредственно связан с шириной спектрального окна, часто называемый шириной полосы окна. При увеличении этого показателя большее количество спектральных ординат усредняется, следовательно, результирующая оценка становится более плавной, более стабильной и имеет меньшую дисперсию. До тех пор, пока спектр остается плоским, смещение также увеличивается, потому что все больше и больше спектральных ординат дают свой вклад в сглаживание. Таким образом, здесь приходится идти на компромисс между снижением дисперсии и смещением (типичная ситуация при статистических оценках).
В общем случае можно считать, как это следует из выражения (5.40), что выборочный спектр определен на любой частоте ω между - π и +π. Таким образом, запишем общий сглаженный спектр в виде следующего интегрального выражения
где WN (λ) - спектральное окно, удовлетворяющее условиям
(5.45)
В случае если спектр приблизительно постоянен в пределах ширины полосы окна, тогда первое из уравнений (5.45) дает
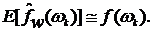
Для дисперсии можно записать следующее выражение
В соответствии с последним из равенств (5.45) следует, что 
при 
, следовательно, 
является состоятельной оценкой спектра f (ω).
Отметим, что спектральные ординаты на двух различных частотах ω и λ являются коррелированными, так как они могут содержать некоторые общие члены при сглаживании. Вследствие этого ординаты выборочного спектра на различных частотах Фурье - независимы, однако ковариация между сглаженными спектральными ординатами пропорциональна величине перекрытия между спектральными окнами с центрами на частотах ω и λ. Ковариация является большой в случае значительного перекрытия спектральных окон и малой - в противном случае.
Сглаживание во временной области
Из приведенного выше уравнения (5.20) следует, что спектр является преобразованием Фурье (ПФ) от АКВФ. Для оценки спектра можно заменить теоретическое значение АКВФ ее выборочной оценкой и воспользоваться формулой (5.40). Тогда альтернативой сглаживанию спектра в частотной области служит применение весового окна W (h) к выборочной автоковариации, т.е.
Поскольку выборочная АКВФ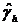 
- симметрична и менее надежна для больших значений h, весовая функция W (h) должна быть выбрана симметричной с весами, обратно пропорциональными величине h. Таким образом, имеем
(5.46)
где весовая функция W (h) выбрана так, чтобы быть абсолютно суммируемой последовательностью, т.е.
Абсолютная суммируемость обычно следует из ограниченной четной непрерывной функции W (х), удовлетворяющей условиям
Величина М является точкой усечения, которая зависит от размера выборки N. Весовое окно WN (h) для автоковариаций называется лаговым окном. Спектральное и лаговое окна тесно связаны между собой вследствие того, что АКВФ определяется через обратное ПФ, т.е.
(5.47)
Таким образом,
где 
. (5.48)
Равенство (5.48) определяет спектральное окно. Из последнего выражения ясно, что спектральное окно является ПФ от лагового окна, а лаговое окно - обратным ПФ от спектрального окна, т.е.
. (5.49)
Следовательно, эти два окна образуют пару преобразования Фурье.
Рассмотрим некоторые наиболее часто используемые окна.
1. Прямоугольное окно. Прямоугольное или усеченное лаговое окно, имеющее вид
(5.50)
где М - точка усечения меньшая, чем (N – 1).
Выражение (5.50) выводится из непрерывной функции
Из выражения (5.48) соответствующее спектральное окно определяется как
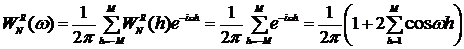
После некоторых тригонометрических преобразований получим
(5.51)
Прямоугольное лаговое и спектральное окна показаны на рис.5.7.
а) б)
Рис.5.7 Прямоугольное лаговое (а) и спектральное (б) окна
Из рис.5.7 видно, что спектральное окно имеет основной максимум на частоте ω = 0 высотой (2 М + 1)/2 π, нули - на частотах ω = ± 2 j π/(2 М + 1) и боковые лепестки уменьшающейся амплитуды приблизительно на частотах ω = ± (4 j + 1)/(2 М + 1) для j = 1, 2, …. Вследствие этого сглаженная оценка спектра, полученная с помощью прямоугольного окна, может приводить к отрицательным значениям на некоторых частотах. Поскольку спектр определяет собой энергию сигнала, этот результат нежелателен.
2. Окно Бартлетта. Бартлетт предложил лаговое окно следующего вида
(5.52)
Окно Бартлетта основано на треугольной функции
поэтому временное окно, определяемое равенством (5.52), иногда называют треугольным окном.
Соответствующее спектральное окно имеет вид
(5.53)
Временное и спектральное окна Бартлетта приведены на рис.5.8.
а) б)
Рис.5.8 Окна Бартлетта (а - временное; б - спектральное)
Вследствие того, что спектральное окно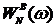 
неотрицательно, получаемая оценка спектра также всегда неотрицательна. Кроме того, сравнение формул (5.51) и (5.53) показывает, что боковые максимумы окна Бартлетта меньше, чем соответствующие характеристики у прямоугольного окна. Эффект больших боковых лепестков позволяет оценке спектра 
получить больший вклад в процесс сглаживания на частотах, удаленных от ω. Следовательно, результирующая оценка спектра может отражать значимые спектральные компоненты на других частотах, отличных от ω. С учетом того, что боковые максимумы формируются преобразованием Фурье от кривых, содержащих острые края, общий принцип выбора временного окна сводится к устранению таких функций.
3. Окно Блекмэна-Тьюки. В этом случае весовое окно имеет следующий вид
(5.54)
В основу этого окна положена непрерывная весовая функция
Здесь, как и в предыдущем случае, М - точка усечения для выборочной АКВФ, а постоянная а выбирается из диапазона 0 < а ≤ 0,25 для всех h. Соответствующее спектральное окно получается таким:
.
После некоторых алгебраических преобразований последнее выражение становится равным
(5.55)
Из выражения (5.55) видно, что спектральное окно Блекмэна-Тьюки представляет собой взвешенную линейную комбинацию прямоугольных весовых окон на частотах (ω – π/ M), ω и (ω + π/ M), т.е.
(5.56)
где 
определяется выражением (5.51).
Очевидно, как и в случае прямоугольного весового окна, оценка спектра Блекмэна-Тьюки может быть отрицательной на некоторых частотах.
Укажем две разновидности последнего окна. Блекмэн-Тьюки назвали окно (5.54) при а = 0,23 окном Хэмминга, который был одним из соавторов Тьюки в этой области. При этом окно Хэмминга становится равным
(5.57)
При другом значении параметра а = 0,25 приходим к окну Хэннинга, названного так в честь австрийского метеоролога Д. Хэнна. В этом случае окно приобретает вид
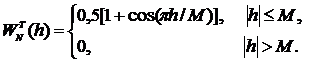(5.58)
Временное и спектральное окна Хэннинга приведены на рис.5.9.
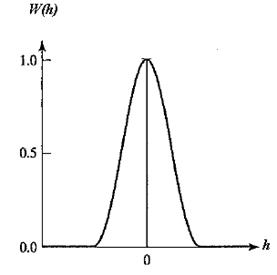
а) б)
Рис.5.9 Окна Хэннинга (а - временное; б - спектральное)
4. Окно Парзена. Это временное окно имеет вид
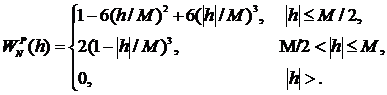(5.59)
Выражение (5.59) основано на непрерывной весовой функции
такого вида
Соответствующее спектральное окно для четных значений М определяется как
(5.60)
При больших значениях М выражение (5.60) может быть аппроксимировано следующим образом
На рис.5.10. показаны временное и спектральное окна Парзена.
а) б)
Рис.5.9 Окна Парзена (а - временное; б - спектральное)
Качество сглаженного спектра определяется формой окна (формой весовой функции) и шириной окна (точкой усечения). Спектральные оценки, полученные для окон одинаковой формы и разной ширины, будут различными. Таким образом, при сглаживании спектра рассматривается вопрос не только выбора спектрального окна с требуемой формой, но также и ширины этого окна. Последнее обстоятельство является часто более критичным и трудным при анализе временных рядов, так как для заданной формы окна нет единственного критерия выбора оптимальной ширины полосы. Кроме того, большая ширина дает более сглаженную оценку с меньшей дисперсией; с другой стороны, более узкая ширина полосы приводит к меньшему смещению и, следовательно, к более высокому разрешению спектральных оценок. Необходим компромисс между высокой стабильностью и высоким разрешением. Для разрешения этого противоречия могут быть предложены следующие шаги:
1. Выбор спектрального окна с приемлемой и требуемой формой.
2. Начальное вычисление спектральных оценок, используя большую ширину окна.
3. Пересчет оценок с применением постепенно уменьшающейся ширины до тех пор, пока не будут достигнуты требуемая стабильность и разрешение.
Такая процедура часто называется сужением окна " window closing ".
Пример 5.2. Рассмотрим применение различных окон для оценки спектра на динамике изменения индекса РТС за 2013г. На рис.5.10 показан временной график этого ряда (точки обозначают еженедельные значения) [8].
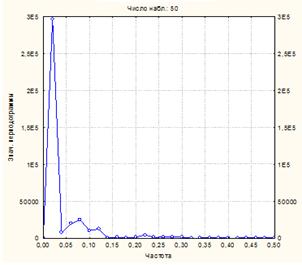
На рис.5.11 показаны спектральная плотность и периодограмма этого ряда, полученные при использовании окна Хемминга.
Рис.5.10 Изменение индекса РТС за 2013г.
а) б)
Рис.5.11 Спектральная плотность (а) и периодограмма (б) индекса РТС (окно Хемминга)
В табл.5.2 приведены значения десяти наибольших значений рассчитанных показателей при использовании окна Хемминга.
Таблица 5.2 Результаты спектрального анализа
Как следует из графиков и табл.5.2, наибольший период определяется длиной ряда (Т = 50 нед.), т.е. никаких сезонных колебаний на протяжении наблюдений не просматривается.
Результаты такой же операции, но выполненной с применением окна Парзена, показаны на рис.5.12 и в табл.5.3.
а) б)
Рис.5.12 Спектральная плотность (а) и периодограмма (б) индекса РТС (окно Парзена)
Таблица 5.3 Результаты спектрального анализа
Как видно из сопоставления приведенных графиков и таблиц, вид спектра и периодограммы несколько различаются и, следовательно, зависят от используемых окон.
