Рассмотрим спектры некоторых стационарных временных процессов.
1. Белый шум (white noise, WN)
Этот процесс подчиняется нормальному закону с нулевым средним и дисперсией σ2, т.е. если {Z t } ~ WN (0, σ2), тогда γ(0) = σ2 и γ(h) = 0 для всех | h | > 0. В этом случае спектр, рассчитанный с помощью формулы (5.20), становится равным
. (5.22)
Таким образом, спектр белого шума является постоянным и представляет собой горизонтальную линию, так как каждая частота в спектре вносит равный вклад в дисперсию процесса.
Рис.5.2 Спектр белого шума
2. Процесс авторегрессии первого порядка AR (1)
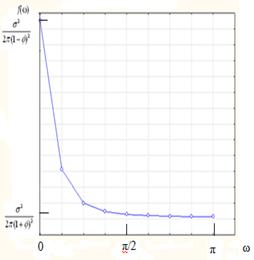
Для модели вида Xt = 
Xt - 1 + Zt, где { Zt } ~ WN (0, σ2), из выражения (2.7) для АКВФ следует, что 
, р = 0, ± 1, ±2, …. Тогда, используя формулу (5.20) и выражение (1.447) из [4], после некоторых алгебраических преобразований получим
На рис.5.3 приведены графики спектра модели А R (1) для значений 
= 0,8 и = - 0,8 при 0 ≤ ω ≤ π вместе с АКФ этой модели.
а) = 0,8
б) = - 0,8
Рис.5.3 Автокорреляционные функции и спектры модели А R (1) (а - =0,8; б- = - 0,8)
Из графиков, представленных на рис.5.3, видно, что форма спектра зависит от знака . При > 0 спектральная плотность - сравнительно большая на низких частотах и малая - на высоких. Это объясняется тем, что при = 0,8 процесс А R (1) имеет положительную АКФ с большим значением при лаге, равном единице, что делает ряд плавным с несколькими высокочастотными компонентами. (Графики АКФ взяты из главы 2, рис.2.2). С другой стороны, при < 0 АКФ имеет относительно большую отрицательную величину, формируя ряд, который быстро флуктуирует вокруг своего среднего значения. Здесь ряд дает большой вклад на высокочастотных составляющих, что демонстрируется величиной спектра на частоте вблизи π. Таким образом, низкочастотный доминирующий спектр определяет относительно плавный ряд в то время, как высокочастотный преобладающий спектр соответствует более изрезанному ряду (сравни рис.2.9 и 2.12 из главы 2).
При →1 процесс А R (1) стремится к модели случайного блуждания Xt = Xt - 1 + Zt. Для этой модели спектр определяется выражением
(5.24)
Строго говоря, модель случайного блуждания не имеет спектра, так как АКВФ не является абсолютно суммируемой. Тем не менее, выражение (5.24) определяет неотрицательную четную функцию, обладающую "хорошим" поведением всюду, кроме точки ω = 0, где пик функции становится бесконечным по амплитуде.
3. Процесс скользящего среднего первого порядка МА (1)
Для модели (2.20), определяющей процесс МА (1), имеем
Xt = at + θ1 а t – 1. (2.20)
Xt = Zt + θ Zt – 1, где { Zt } ~ WN (0, σ2).
Модель МА (1) характеризуется АКФ следующего вида (см. формулу (2.22):
С использованием выражения (5.20) проведем алгебраические преобразования, подобные выполненным для модели А R (1), в результате чего получим
(5.25)
На рис.5.4 показаны рассчитанные спектры модели МА (1) при значениях θ = 0,8 и θ = - 0,8. Здесь же приведены графики разыгранных процессов МА (1) при этих значениях коэффициента θ. Графики АКФ в этом случае не приводятся, поскольку они становятся нулевыми при лаге больше двух.
а)
б)
Рис. 5. 4 Спектры и разыгранные модели МА (1) (а - θ = 0,8; б- θ = - 0,8)
Из приведенных графиков видно, что при θ > 0 спектр сосредоточен в области низких частот, а ВР модели МА (1) при положительной АКФ является относительно плавным. В другой ситуации, при θ < 0 спектральная плотность сосредоточена в области высоких частот, а ВР модели МА (1) при отрицательной АКФ становится достаточно изрезанным.
4. Гармонический сигнал с искажениями
Положим, что такой сигнал описывается выражением
(5.26)
где ω0 - постоянная частота из диапазона (0,π); φ - случайная переменная, имеющая равномерное распределение в интервале [0,2π].
Отметим, что для единичной реализации φ - фиксированная величина, и уравнение (5.26) определяет чисто детерминированный процесс. АКВФ этого ряда имеет следующий вид
Из последнего равенства следует, что АКВФ при увеличении h не стремится к нулю. Следовательно, процесс (5.26) характеризуется "долгой памятью" ВР. Для этой модели мощность всего процесса концентрируется на частоте ω0.
Поскольку среднее значение E (Xt) = 0, то дисперсия процесса определяется как V а r (Xt) = E (Xt 2) = 1/2, поэтому спектральная функция распределения выражается следующим образом
Укажем, что дисперсию процесса можно найти через АКВФ: V а r (Xt) = γ (0) = 1/2. Поскольку СФР представляет ступенчатую функцию, то она не имеет производной в точке ω0. Если, тем не менее, попытаться найти спектр через преобразование Фурье, приходим к выводу, что
Такой результат и ожидался, так как сумма 
не сходится при ω = ω0. Иначе говоря, спектр модели (5.26) не определен на частоте ω0.
5. Смесь детерминированного и стохастического сигналов
Примем, что сигнал описывается выражением
(5.27)
где ω0 , φ определены также, как для модели (5.26); Zt - случайный процесс с нулевым средним и дисперсией 
.
Для модели (5.27) АКВФ определяется следующим образом
Аналогично предыдущему примеру 
не стремится к нулю при увеличении h, так как Xt содержит периодический детерминированный компонент. Для получения СФР F (ω) модели (5.27) учтем следующее. Если процесс содержит детерминированный синусоидальный компонент на частоте ω0, тогда на этой частоте будет ступенчатое увеличение F (ω), равное вкладу в дисперсию этой составляющей. При монотонном возрастании F (ω) последняя может быть разложена на две функции F 1(ω) и F 2(ω) таким образом, что
где F 1(ω) - ниспадающая непрерывная функция; F 2(ω) - ниспадающая ступенчатая функция.
Эта декомпозиция обычно соответствует теореме разложения Волда, когда F 1(ω) соответствует недетерминированному компоненту процесса, а F 2(ω) - детерминированной составляющей. Теперь можно воспользоваться последней формулой для получения СФР всей модели, так как детерминированный компонент cos(ω0 t + φ) имеет следующую СФР
Стохастическая составляющая Zt имеет СФР, равную
что является результатом интегрирования выражения (5.22).
Таким образом, комбинированная СФР для модели (5.27) определяется как
Также, как и в предыдущем примере, СФР имеет ступенчатый подъем на частоте ω0, и поэтому спектр не определен на этой частоте.
