Спектры стационарных процессов

Глава 5 Спектральный анализ временных рядов

 

5.1 Преобразование Фурье. 2

5.2   Спектры стационарных процессов. 7

5.3   Примеры спектров временных рядов. 13

5.4 Периодограммный метод оценки спектров. 21

5.5 Сглаживание спектра. 29

5.6 Исключение сезонности преобразованием Фурье. 43

 

    Выше были рассмотрены стационарные временные ряды, которые описываются моделями А R (p), M А (q), А RM А (p, q). Для рассмотрения их свойств во временной области служат автоковариационная или автокорреляционная функции. В данной главе вводится дополнительная характеристика, называемая спектральной плотностью мощности   или просто спектром, с помощью которой оцениваются частотные свойства ВР. Спектральное представление стационарного ВР, по существу, разлагает этот ряд в сумму синусоидальных компонентов с некоррелированными случайными коэффициентами. Спектральная декомпозиция стационарных процессов является аналогом представления Фурье детерминированных функций. Анализ стационарных процессов посредством их спектрального представления обычно рассматривается как частотный анализ конкретного ряда или спектральный анализ. Такой прием обеспечивает альтернативный путь анализа ВР, который в ряде случаев оказывается более информативным. 

    Определение скрытых закономерностей во временных рядах является сложной задачей, и спектральный анализ представляет собой мощный инструмент для выполнения этой задачи. По сравнению с традиционными методами анализа временных рядов спектральный анализ имеет ряд преимуществ, так как позволяет одновременно найти частоту различных периодических составляющих и их амплитуду. 

 

Преобразование Фурье

 

Чаще всего сигналы, предназначенные для анализа, представлены во временной области, т.е. сигнал есть функция времени, и наблюдаемая совокупность данных есть ВР. Таким образом, при отображении ВР на графике одной из координат является ось времени, а другой - ось амплитуд. Это представление сигнала называется амплитудно-временным. Однако для большинства приложений амплитудно-временное представление не является наилучшим. Во многих случаях наиболее значимая информация скрыта в частотной области. Для выполнения анализа ВР в частотной области кратко рассмотрим преобразования Фурье. Укажем основные соотношения, касающиеся рядов и интегралов Фурье [1]. 

Периодическая функция определяется как 

                                                                               (5.1)

где Т - период функции; n  - любое целое число (положительное или отрицательное). 

    Формула (5.1) определяет основное свойство периодической функции, заключающееся в том, что процесс периодически повторяется и такая повторяемость имеет место для всех времен от - ∞ до + ∞. Таких периодических явлений в строгом смысле в природе не существует, и функция, определяемая равенством (5.1), является математической абстракцией. 

    Всякая периодическая функция может быть представлена в виде ряда, состоящего из тригонометрических функций

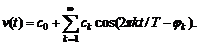                                                      (5.2)

    Как следует из равенства (5.2), периодическая функция v (t) представлена суммой слагаемых, каждое из которых определяет собой синусоидальное колебание с амплитудой c_k и начальной фазой φ _k. Частоты колебаний, из которых составляется функция v (t), образуют гармоническую последовательность, т.е. частоты всех составляющих кратны основной частоте 1/ T. Отдельные составляющие называются гармониками. Колебание с частотой 1/ T определяет первую гармонику, с частотой 2/ T - вторую гармонику и т.д.

    Равенство (5.2) может быть записано в другой форме

                                   (5.3)

где а _k = c_k cos φ _k; b_k = c_k sin φ _k; c_k = (а _k ² + b_k ²)^1/2; tg φ _k = b_k /а _k. Коэффициенты а _k и b_k вычисляются по формулам

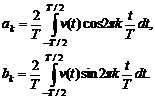
    Величина с ₀ определяет среднее значение функции за период и вычисляется по формуле

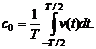
    Выражения (5.2), (5.3) определяют ряд Фурье, который может быть записан также в комплексной форме 

                                                                   (5.4)    

где 2 C_k = c_k e ^{- jφk} = а _k  - jb_k; c ₀ = C ₀. Величина 2 C_k является комплексной амплитудой, которая определяется по формуле

                                                           (5.5)

    Ряд Фурье дает разложение периодической функции по тригонометрическим. Такое разложение может быть обобщено и на случай непериодической функции, что достигается применением предельного перехода при T → ∞. Последнее утверждение справедливо, поскольку непериодическую функцию можно рассматривать как предельный случай периодической функции при неограниченно возрастающем периоде.

    Подставим в формулу (5.4) значение C_k из (5.5):

                                                                     (5.6)

    В последней формуле перейдем к пределу, устремляя T к бесконечности. Вместо 1/ Т введем круговую основную частоту           ω₁ = 2π / Т, которая определяет частотный интервал между соседними гармониками. При предельном переходе проведем замену по следующей схеме: T → ∞, ω₁ → d ω, 2π k / Т → ω, где ω - текущая частота, изменяющаяся непрерывно; d ω - ее приращение.

    При таком преобразовании сумма в выражении (5.6) трансформируется в интеграл, в результате чего получим

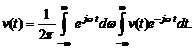
    Последнее равенство перепишем в виде

                                                                           (5.7)

где               

                                                                                (5.8)

    Выражения (5.7), (5.8) представляют собой основные формулы спектрального анализа. Эти равенства - пара преобразований Фурье, которые связывают между собой две функции: вещественную функцию времени v (t) и комплексную функцию частоты V (ω). Формула (5.7) определяет интеграл Фурье в комплексной форме, а ее смысл заключается в том, что функция v (t) представлена суммой синусоидальных составляющих. Но функция v (t) предполагается непериодической, поэтому она может быть представлена только суммой бесконечно большого числа малых колебаний, близких по частоте. 

    Отметим, что ряд Фурье определяет периодическую функцию суммой бесконечного числа синусоид, но с частотами, имеющими конкретные дискретные значения. В то же время интеграл Фурье представляет непериодическую функцию в виде суммы бесконечного числа синусоид с непрерывной последовательностью частот, т.е. в составе непериодической функции имеются все частоты. Еще одна особенность, которая различает интеграл и ряд Фурье, состоит в том, что ряд Фурье есть периодическая функция в виде суммы периодических же составляющих; интеграл Фурье - непериодическая функция в виде суммы периодических составляющих. Таким образом, в случае интеграла Фурье сумма не обладает существенным свойством своих слагаемых, что необходимо иметь в виду при проведении спектрального анализа. 

    Спектр периодической функции можно представить графически. Для этого перепишем формулу (5.2) в виде 

                                                    (5.9)

где ω₁ = 2π / T  - основная частота.

    Из (5.9) видно, что сложная периодическая функция v (t) определяется набором величин c_k и φ _k. Совокупность величин c_k называется спектром амплитуд, совокупность величин φ _k - спектром фаз. Наиболее часто используется спектр амплитуд, поэтому при упоминании спектра подразумевают именно его.

    Для графического представления выберем координаты c_k и ω = k ω₁. В этой системе координат спектр изображается набором дискретных точек, так как каждому значению k ω₁ соответствует определенное значение c_k. График из отдельных точек  неудобен для просмотра, поэтому принято отображать амплитуды отдельных гармоник вертикальными отрезками соответствующей длины (рис.5.1).

Рис.5.1 Спектр периодической функции

    Спектр, показанный на рис.5.1, называется дискретным. Кроме того, этот спектр - гармонический, т.е. частоты отдельных гармоник находятся в простых кратных соотношениях.

    При рассмотрении спектров непериодических функций учтем, что в результате предельного перехода от ряда к интегралу Фурье интервалы между отдельными спектральными линиями неограниченно сокращаются, линии сливаются, и вместо дискретных точек спектр изображается непрерывной кривой. Такой спектр называется сплошным. Здесь необходимо внести следующее уточнение. В формуле (5.7) подынтегральная функция выражает колебание с бесконечно малой амплитудой dC    

    Отсюда находим, что V (ω) = dC / d ω. Следовательно, величина V (ω) выражает не непосредственно амплитуду, а спектральную плотность. Однако чаще всего V (ω) называют комплексным спектром непериодической функции, а абсолютное значение (модуль) этой величины Φ (ω)= | V (ω)| просто спектром.

    Подводя итоги этому параграфу, можно сказать, что применение преобразования Фурье (ПФ) очень наглядно, так как все необходимые свойства и формулы выписываются с помощью всего двух действительных функций sin t, cos t (или одной комплексной                   exp (it) = cos t + i sin t, i = (-1)^0,5) и достаточно легко доказываются.

Спектры стационарных процессов

 

    Обратимся теперь к рассмотрению спектров стационарных процессов. Положим, что ВР содержит периодическую синусоидальную составляющую с известной длиной волны и стационарную случайную составляющую. Тогда ВР можно описать моделью 

                                                                                   (5.10)

где R - амплитуда;  - фаза колебания; { Z_t }- стационарный случайный ряд.      

    Выражение (5.10) описывает достаточно простую модель, но на практике вариации ВР  обусловлены изменениями на различных частотах. Например, объем продаж какого-либо товара может содержать недельные, месячные, годовые и другие циклические флуктуации. Иначе говоря, результирующий ВР содержит вариации на высоких, средних и низких частотах, поэтому естественно обобщить уравнение (5.10) до такого вида   

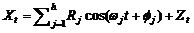                             ,                               (5.11)

где R_j, ф _j   обозначают, соответственно, амплитуду и фазу на частотах .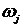

Для применения теории стационарных процессов к моделям, которые описываются уравнением типа (5.11), обычно допускается, что значения { R_j } являются некоррелированными случайными величинами с нулевым средним или { ф } - случайные величины с равномерным распределением на интервале (0, π).

    Модель в уравнении (5.11) можно представить в виде суммы синусных и косинусных членов, т.е. 

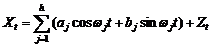            ,                                         (5.12)

где  и

    Сравнение формул (5.3) и (5.12) показывает, что последняя модель отличается наличием члена Z_t, определяющим стационарную случайную составляющую, и верхним пределом суммы.  Возникает вопрос о количестве членов под знаком суммы:  почему только конечное число частот включены в выражение (5.12). Можно показать [2], что при         h → ∞ любой дискретный стационарный процесс, измеренный через равные   интервалы, представляется в виде

               ,                       (5.13)

где u (ω), v (ω) - некоррелированные непрерывные процессы, которые определены на интервале (0, π).

    Уравнение (5.13) называется спектральным представлением процесса, содержащим стохастические интегралы, что требует значительных математических усилий. Для упрощения расчетов примем, что X_t   представляет собой сумму ортогональных синусоидальных членов. Кроме того, укажем еще на одно обстоятельство, относящееся к верхнему пределу в уравнении (5.13). Для непрерывного процесса верхний предел действительно должен быть равен ∞, но для дискретного процесса, наблюдаемого через равные интервалы времени, без потери общности пределы интегрирования ограничим диапазоном (0,π), поэтому    

  Частота ω = π называется частотой Найквиста. Для дискретного процесса, наблюдаемого через равные интервалы времени Δ t, эта частота равна π / Δ t.

    Основная цель введения спектрального представления в уравнение (5.13) заключается в том, чтобы показать, как каждая частота из диапазона (0...π) вносит свой вклад в вариацию процесса. Однако процессы u (ω), v (ω) в формуле (5.13) имеют малый практический интерес. Вместо них введем единственную функцию F (ω), называемую спектральной функцией распределения (СФР), которая связана с автоковариационной функцией и дает описание частотных свойств стационарного процесса. Это следует из теоремы Винера-Хинчина [3], которая гласит, что для любого стационарного процесса с автоковариационной функцией (АКВФ) γ(h) существует монотонно возрастающая функция F (ω) такая, что  

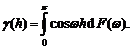                                                                 (5.14)

    Уравнение (5.14) определяет спектральное представление АКВФ. Можно показать, что функция F (ω) имеет прямую физическую интерпретацию: она дает вклад в дисперсию ряда для каждой из частот в диапазоне (0,π). Если изменений на отрицательных частотах не допускается, тогда

    Для дискретного процесса, регистрируемого через равные интервалы времени, наивысшая возможная частота есть частота Найквиста π, поэтому все вариации рассчитываются для частот, меньших π. В этом случае 

    Последний результат можно получить также из уравнения (5.14), положив h = 0, что дает 

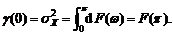
    В диапазоне частот между ω = 0 и ω = π функция F (ω) монотонно увеличивается. Иногда термин "спектральная функция распределения" дополняют словом "мощность", образуя новый термин: СФР мощности. Такое словосочетание исторически происходит от употребления в среде инженеров-электриков и связано с прохождением электрического тока через сопротивление. Для синусоидального входа мощность прямо пропорциональна квадрату амплитуды колебания. Для более общего входа СФР мощности описывает, как мощность распределена по частоте. В случае  ВР дисперсия рассматривается как общая мощность.

    Для недетерминированных дискретных стационарных процессов СФР является постоянной функцией в диапазоне (0...π) и поэтому может быть дифференцирована по ω. Обозначим производную как f (ω), которая имеет вид

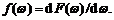                                                                 (5.15)

    Полученное выражение определяет функцию спектральной плотности мощности, название которой часто сокращают до спектра.  Если f (ω) существует, то выражение (5.14) представляется в виде

                                                              (5.16)

    Выражение (5.16) проще интегрировать, чем при использовании формулы (5.14). Положив h = 0, имеем

                                                        (5.17)

    Физическая интерпретация спектра заключается в том, что он определяет вклад в дисперсию от всех частотных компонентов в данном диапазоне. При построенной зависимости спектра от частоты уравнение (5.17) показывает, что площадь под кривой равна дисперсии процесса. Выбросы спектра на конкретных частотах указывают на важный вклад соответствующей составляющей в общую дисперсию. Строго говоря, F (ω) может быть не дифференцируема на граничных точках 0 и π, поэтому необходимо указать открытый интервал интегрирования (0...π), чем включать его границы.

    Пример спектра показан на рис.5.2 вместе с соответствующей нормированной СФР.

        

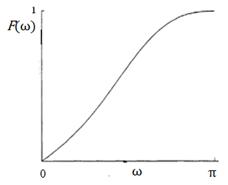
                                    а)                                                               б)                                             

Рис.5.2 Спектр (а) и спектральная функция распределения (б)

      

Важно отметить, что АКВФ γ(h)   и спектр f (ω) являются эквивалентными способами описания стационарных стохастических процессов. С практической точки зрения они дополняют друг друга. Обе функции содержат одинаковую информацию, но выражают ее различными путями. В некоторых ситуациях предпочтительнее временной подход к описанию ряда, в других - частотный.

    Уравнение (5.16) выражает связь между γ(h) и f (ω) в виде преобразования Фурье. При допущении об абсолютной суммируемости АКВФ γ(h), т.е. , спектр определяется как   

                                                          (5.18)

Таким образом, спектр есть преобразование Фурье от АКВФ. Поскольку γ(h) является четной функцией h, последнее выражение можно привести к виду 

                                              (5.19)

        

При использовании уравнения (5.19) для процесса, содержащего детерминированную составляющую на частоте ω₀, сумма   не будет сходиться при ω = ω₀. Это следует из того, что F (ω) изменяется ступенчатым образом и, следовательно, не дифференцируема на частоте ω₀. Таким образом, производная f (ω) не определена на частоте ω₀. В литературе приводятся и другие определения спектра, большинство из которых отличаются от уравнения (5.19) величиной постоянного множителя и диапазоном изменения f (ω). Наиболее часто приводятся такие определения

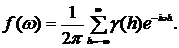                                                     (5.20)

Обратное преобразование для АКВФ имеет вид

                                                               (5.21)

Уравнения (5.20), (5.21) образуют пару преобразований Фурье и являются общепринятой формой соотношения Винера-Хинчина.

В заключение этого параграфа укажем основные свойства спектра:

1. 1 f (ω) - непрерывная вещественная неотрицательная функция, т.е. | f (ω)| = f (ω). 

2. f (ω) является четной функцией, т.е. f (ω) = f (- ω).

3. f (ω) = f (ω + 2π), следовательно, f (ω) - периодическая функция с периодом, равным 2π.

4. Из выражения (5.21) имеем для дисперсии 

откуда видно, что спектр f (ω) может быть интерпретирован как декомпозиция дисперсии процесса. Член   является вкладом в дисперсию, связанным с составляющей процесса на частотах из интервала .