Многие ВР разной природы (экономические, метеорологические и др.) содержат сезонные явления, которые повторяются через регулярные периоды времени. Наименьший временной период для таких повторных явлений называется сезонным периодом. Например, квартальные продажи мороженого значительны каждое лето, и ВР продаж повторяет это явление каждый год, определяя сезонный период, равный 4. Пик продаж игрушек приходится на декабрь (рождественские и новогодние подарки), и в этом случае сезонный период составляет 12 мес. На сезонность ВР влияют такие факторы, как погода, которая приводит к изменению потока туристов в течение года и вариациям в сельском хозяйстве.
Методы, описанные выше для оценки и исключения тренда, могут быть адаптированы для исключения сезонности в общей модели вида (1.5). Рассмотрим следующие приемы.
Оценка тренда и сезонного компонента.
Шаг 1. Предположим, что имеются наблюдения { x 1,..., xn } с сезонным периодом, равным d. Вначале оценивается тренд методом скользящего среднего для исключения сезонной составляющей и ослабления шума. Если период d четный, например, d = 2 q, тогда используется следующее выражение
(1.12)
В ситуации, когда период d нечетный, например, d = 2 q +1, формула (1.12) преобразуется к виду
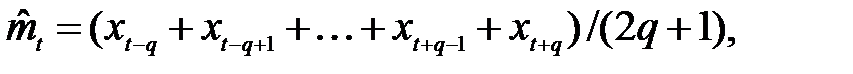
(1.13)
Шаг 2. На этом шаге проводится оценка сезонного компонента. Для каждого k = 1,..., d вычисляется среднее значение отклонений
.
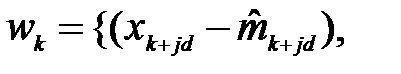
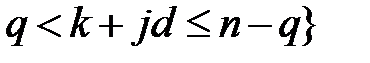Поскольку эти средние отклонения не обязательно дают в сумме нуль, то сезонный компонент оценивается как
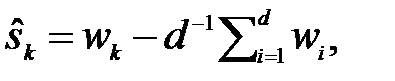k = 1,..., d. (1.13)
Шаг 3. Данные без сезонности затем определяются как разность между исходным рядом и сезонным компонентом, т.е.
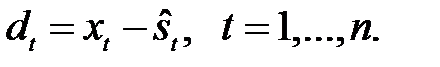(1.15)
Шаг 4. Окончательно переоценивается тренд из десезонных данных, используя, например, метод экспоненциального сглаживания. Сущность последнего сводится к следующему. Для любого фиксированного 
скользящие средние 
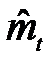, t = 1,..., n определяются рекурсивными выражениями
(1.16)
(1.17)
Применение выражений (1.15), (1.16) называется экспоненциальным сглаживанием, так как рекурсивные выражения означают, что для t ≥ 2 величины 
представляют собой взвешенное скользящее среднее Xt, Xt - 1,..., с экспоненциально уменьшающими весами (за исключением последнего члена).
Различные программы позволяют подогнать полиномиальный тренд 
к данным с устраненной сезонностью. В терминах вновь найденного тренда и оцененного сезонного компонента шумовой ряд (помехи) определяется как
Переоцененный тренд в дальнейшем потребуется для того, чтобы иметь параметрическую форму для тренда, который может быть экстраполирован для целей прогноза и имитации.
Исключение тренда и сезонной составляющей.
Метод дифференцирования, который применялся выше для несезонных данных, может быть адаптирован для сезонных наблюдений периода d введением оператора дифференцирования с лагом d, определяемый как
(1.18)
(Оператор 
не следует смешивать с оператором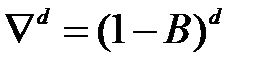 
, рассмотренным ранее).
Применяя оператор 
к модели (1.6) Xt = mt + st + Yt, где { st } имеет период d, получим выражение
которое дает декомпозицию разности 
в составляющие тренда (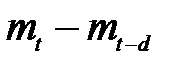
) и помехи (
).
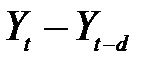Пример 1.4. Провести дифференцирование ряда числа авиапассажиров на протяжении 12 лет с использованием оператора (1.18).
На рис. 1.11 приведены исходный ряд и ряд, полученный после операции дифференцирования.
а) t = 1,.., 144
б) t = 13,.., 144
Рис.1.11 Исходный ряд (а) и ряд после дифференцирования (б; 
)
Как видно из графиков, на рис.1.11.б еще наблюдается неявно выраженный тренд и некоторое проявление сезонности. Для их устранения применим оператор 
к оператору , т.е. совершим трансформацию (). Результат такого двойного дифференцирования показан на рис.1.12, откуда следует, что теперь ряд не показывает ни тренда, ни сезонности. ■
Рис.1.12 Ряд после двойного дифференцирования: ()
Литература
1. Tufte, E. R. The Visual Display of Quantitative Information, Graphics Press, Cheshire, Connecticut, 2001.-197р.
2. Бокс Дж., Дженкинс Г. Анализ временных рядов: прогноз и управление. М.: Мир, 1974. Вып.1.- 406 с.
3.Brown, R. G. Smoothing, forecasting and prediction of discrete time series. Englewood Cliffs, NJ7 Prentice-Hall.1963. - 468р.
4. Gardner Jr.,E.S., Exponential smoothing: The state of the art – Part II. 2005. http://www.bauer.uh.edu/gardner/docs/pdf/Exponential-Smoothing.pdf.
5. Gardner Jr., E. S. Exponential smoothing: The state of the art. Journal of Forecasting, 1985,4, 1 –38.
6. Snyder, R. D. Recursive estimation of dynamic linear statistical models. Journal of the Royal Statistical Society (B), 1985, 47, 272–276.
7. Hyndman, R. J., Koehler, A. B., Snyder, R. D., & Grose, S. A state space framework for automatic forecasting using exponential smoothing methods. International Journal of Forecasting, 2002,18, 439–454.
8.Robinson,P.M. Long-memory Time Series. / in Times Series with Long Memory. / P.Robinson. Oxford, University Press, 2003, 4-32.
9.Palma W. Long-memory Time Series. J.Wiley&Sons, New Jersey, 2007. - 286р.
10. Guide to Seasonal Adjustment with X -12- ARIMA, https://www.google.ru/search?sourceid=navclient&hl, 2007.
11. Forecasting time series with complex seasonal patterns using exponential smoothing. A.M.Livera, R.J.Hyndman, R.D.Snyde. http://www.buseco.monash.edu.au/depts/ebs/pubs/wpapers/ October 2010.
12. Chatfield C. Time-series forecasting. Chapman & Hall/CRC, London, 2000. - 266р.
13. Engle R.F. Autoregressive conditional Heteroscedasticity with estimates of the variance of the United Kingdom inflation. Econometrica, 1982, V. 50, 987–1007.
14. Hippert, H. S., Pedreira, C. E., & Souza, R. C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Transactions on Power Systems, 2001,16, 44–55.
15. Cronea S. F.et al. Advances in forecasting with neural networks? Empirical evidence from the NN3 competition on time series prediction. International Journal of Forecasting, 2011, 27, 635–660.
16. Shyi-Ming Chen, Chia-Ching Hsu. A New Method to Forecast Enrollments Using Fuzzy Time Series. International Journal of Applied Science and Engineering. 2004, 2, 3, 234-244.
17. Дженкинс Г., Ваттс Д. Спектральный анализ и его приложения. М.: Мир, вып.1,1971.-317с.
18. Гренджер К., Хатанака М. Спектральный анализ временных рядов в экономике. М.: Статистика,1972. - 312с.
19. Малла С. Вейвлеты в обработке сигналов. М.: Мир, 2005. — 671с.
20. Percival D., Walden A. Wavelet Methods for Time Series Analysis, Cambridge University Press, 2000. - 594р.
21. Brockwell P. J ., Davis R. A. Introduction to Time Series and Forecasting. Springer Texts in Statistics, Springer-Verlag, New York, 2002. - 450р.
[1] См.ниже главу 3.
[2] Нобелевские лауреаты по экономике 2003г., награжденные «за методы анализа экономических временных циклов методом общих тенденций (коинтеграции)»
