Как было указано выше, первым шагом при анализе ВР является его визуализация. При обнаружении на графике явных разрывов таких, как внезапное изменение уровня, может оказаться полезным анализировать ряд посредством его деления на отдельные однородные сегменты. При наличии отдаленных во времени наблюдений последние должны быть тщательно проверены или даже отброшены, если есть сомнения в их достоверности. В результате изучения графика появляется возможность представления данных как реализации следующего процесса (классическая модель декомпозиции)
Xt = mt + st + at, (1.6)
где mt - медленно изменяющаяся функция, определяющая трендовую составляющую; st - функция с известным периодом, относящаяся к сезонному компоненту; at - составляющая случайного шума.
Тренд присутствует в наблюдаемых данных в том случае, если ряд показывает устойчивый рост или снижение, по крайней мере, на протяжении нескольких последовательных временных периодов. Тренд может быть выявлен как «долговременное изменение над средним уровнем», но четкого математического определения здесь нет.
Сезонная составляющая обычно имеет место в рядах наблюдений с годовым периодом, когда регистрация данных производится еженедельно, ежемесячно или поквартально. В такой ситуации похожие характеристики ВР появляются с годичной периодичностью, например, продажи мороженого имеют ярко выраженный пик продаж в летнее время. Однако заметим, что при современном развитии уровня компьютерной техники и методов извлечения данных очень часто встречаются высокочастотные наблюдения, взятые через малые промежутки времени. В области финансов цены акций изменяются ежедневно или даже еще через меньшие временные интервалы (вплоть до секунд на рынках ценных бумаг). Естественно, что и величина периода, определяющего сезонность, становится достаточно малой. Такие данные важны при эмпирическом изучении рыночной микроструктуры.
Дальнейшая цель анализа ВР сводится к оценке и устранению детерминированных компонент mt и st в надежде, что случайная составляющая at (остаток) окажется стационарным ВР. Тогда можно воспользоваться теорией стационарных процессов для нахождения приемлемой вероятностной модели для процесса at, анализа его свойств и применения вместе с mt и st для прогнозирования и моделирования { Xt }.
Другой путь анализа, предложенный впервые Боксом и Дженкинсом, заключается в неоднократном применении операторов дифференцирования к ряду { Xt } до тех пор, пока подвергнутые дифференцированию наблюдения не образуют реализацию некоторого стационарного ВР { Wt }. Затем можно использовать теорию стационарных процессов для моделирования, анализа и прогноза ряда { Wt }, и, следовательно, исходного процесса.
Тренд временного ряда
Рассмотрим более подробно тренды ВР. Из вышеприведенного определения неясно, что подразумевается под терминами «долговременное» и «средний уровень». Наше восприятие тренда и среднего уровня зависит от длины наблюдаемого ряда. Например, глобальное потепление климата может быть описано как тренд в пределах одной человеческой жизни, но на протяжении сотен лет такие вариации температуры правомерно считать циклическими с низкой частотой изменения.
Обратимся к различным математическим моделям, пригодным для описания тренда [12]. Обозначим через mt локальный средний уровень в момент времени t. Во многих книгах по анализу ВР рассматривается ситуация, где
(1.7)
где α, β - коэффициенты уравнения регрессии.
Такой простой тренд часто называется детерминированным или глобальным линейным трендом. Однако эта модель считается чересчур упрощенной, и ряд авторов предпочитает вместо детерминированной функции использовать так называемые локальные модели. Тогда тренд можно представить изменяющимся во времени стохастическим образом, поэтому в модели (1.7) коэффициенты α и β становятся зависящими от времени
(1.8)
где α t определяет локальное пересечение; β t - локальный наклон.
Модель тренда (1.8) применяется гораздо чаще, так как было установлено, что модель детерминированного линейного тренда (1.7) реже обеспечивает соответствие реальным данным. Существующие компьютерные программы позволяют подгонять данные наблюдений под локальный тренд.
Необходимо указать на некоторую путаницу в литературе по отношению к термину «тренд». Часть авторов считает, что данный термин относится к параметру mt, в то время, как другие аналитики используют этот термин для описания скорости изменения mt, т.е. наклона β или β t. Однако необходимо учесть, что величины mt и β t совершенно различны. В дальнейшем будем считать mt параметром, определяющим локальный уровень.
Альтернативный путь моделирования локального тренда заключается в использовании рекурсивного уравнения, когда вместо уравнения (1.7) глобальный тренд может быть представлен в виде
который более удобен для многих целей.
Если учесть изменение уровня с течением времени и добавить член, определяющий искажения, например, { w 1, t }, то выражение для локального тренда приобретает вид
(1.9)
К формуле (1.9) необходимо добавить второе уравнение, описывающее временную эволюцию {β t }. Это может быть выполнено различными путями. Наиболее часто применяется модель линейного роста, сводящаяся к следующему выражению
где { w 2, t } определяет второй процесс искажений.
Как увидим позже, модель для изменения β t обычно называется моделью случайного блуждания. Рекурсивная форма уравнения (1.9) предпочтительнее по сравнению с уравнением (1.8). Отметим, что уровень mt и скорость роста β t не наблюдаются непосредственно в анализируемых данных, поэтому модель линейного роста справедлива при допущении о наличии ошибки измерений nt в момент регистрации ряда, т.е. вместо mt ряд имеет уровень (mt + nt).
Во многих случаях тренд является нелинейным, например, локальный уровень mt может быть квадратичной функцией, демонстрировать экспоненциальный рост, описываться кривой Гомперца 
или логистической кривой 
.
Тренд может быть оценен двумя различными путями. Во-первых, можно осуществить подгонку наблюдаемых данных методом наименьших квадратов (МНК) под одну из упомянутых выше параметрических функций, например, полиномиальную, кривую Гомперца или логистическую кривую. Затем вычесть подогнанные значения тренда из наблюдаемых данных для нахождения приемлемой модели стационарного ВР, которой можно описать остатки [21].
Пример 1.2. Подобрать квадратичную функцию под смоделированные данные: 
, где a - нормально распределенная случайная величина с нулевым средним и единичной дисперсией.
На рис.1.9 приведены результаты операции подгонки исходных данных под квадратичную функцию. Последняя, как видно из табл.1.2, имеет вид
Здесь же показан график остатков между исходными данными и подогнанной кривой.■
а) б)
Рис.1.9 Подгонка данных квадратичной функцией (а) и остатки (б)
Таблица 1.2 Результаты регрессионного анализа
Во-вторых, можно исключить тренд путем дифференцирования ряда, что сводится к вычитанию предыдущего значения ряда из текущего, т.е.
(1.10)
где B - оператор сдвига назад, равный
BXt = Xt -1 . (1.11)
После этого необходимо найти подходящую стационарную модель для трансформированного ряда.
Степени операторов В и 
определяются очевидным образом:
Если оператор применить к функции линейного тренда 
, тогда получим постоянную величину, так как
Таким же образом любой полиномиальный тренд степени k может быть понижен до постоянной величины применением оператора 
.
Пример 1.3. Провести дифференцирование ряда из примера 1.2.
На рис.1.10 приведены графики ряда, полученного после двух последовательных операций дифференцирования. Как видно, после второй операции дифференцирования тренд уже не просматривается, т.е. ряд становится стационарным. ■
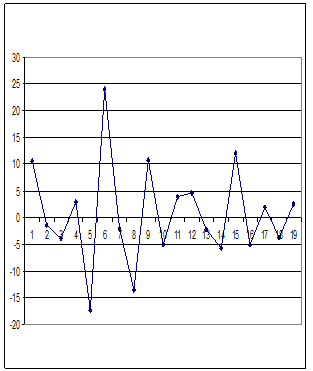
а) б)
Рис.1.10 Результат дифференцирования (а – первая операция; б - вторая операция)
Важно отметить, что устранение тренда зависит от наличия или отсутствия сезонности в рассматриваемом ряде. При наличии сезонности аналитик должен решить, измерять или устранять сезонность перед или после оценки тренда. На практике полезно воспользоваться итеративной процедурой, сводящейся к следующему. Вначале определяются предварительные оценки тренда и сезонности с помощью достаточно простых процедур, например, простого скользящего среднего. Затем эти оценки уточняются посредством более сложных приемов сглаживания до тех пор, пока более приемлемые оценки тренда и сезонности не достигаются. Таким образом, устранение тренда и сезонности являются неразрывно связанными процессами, отражая тот факт, что нет единственного способа декомпозиции вариации ряда в тренд и сезонность. Это приводит к необходимости более глубокого рассмотрения сезонности ВР.
