Пусть { Х t } является стационарным ВР. Определим автоковариационную функцию (АКВФ) ряда { Х t } при лаге (временном разделении) h как
γ X (h) = Cov (Х t+h, Х t).
Автокорреляционная функция (АКФ) ряда { Х t } при лаге h есть
ρ Х (h) = γ X (h) / γ X (0) = Cor (Х t + h, Х t).
Можно показать, что для стационарного процесса АКВФ γ X (h) и АКФ ρ Х (h) обладают следующими свойствами:
1. γ X (0) = Var (Xt); ρ Х (0) = 1.
2. 
3. γ X (h) = γ X (- h), ρ Х (h) = ρ Х (- h) для всех h, т.е. γ X (h) и ρ Х (h) являются четными функциями и, следовательно, симметричны относительно лага h = 0. Это свойство следует из того факта, что временная разница между Х t и Х t + h является такой же, как и между Х t и Х t - h.
Несмотря на то, что АКФ можно вычислить для некоторых простых моделей ВР, на практике обычно начинают с анализа наблюдаемых данных { x 1, x 2,..., xn }. Для оценки степени зависимости данных и подбора модели, которая отражает связь этих наблюдений, одним из значимых и важных средств является использование выборочной АКФ. В случае, когда данные представляют реализации стационарного ВР, выборочная АКФ дает оценку АКФ для { Х t }. Такая оценка может быть использована для отбора из многих возможных моделей стационарных ВР приемлемого кандидата для отображения зависимости в данных. Например, при значениях выборочной АКФ, близких к нулю для ненулевых лагов, подходящей моделью для описания таких наблюдений может служить шумовой сигнал, в котором даже близкие по временному смещению значения мало связаны между собой.
Приведем формулы для вычисления выборочной АКФ. Пусть x 1, x 2 ,..., xn являются наблюдениями ВР. Выборочное среднее есть
Выборочная АКВФ определяется как
Для выборочной АКФ имеем
Пример 1.1. На рис.1.6 показан график 100 значений ВР, смоделированных из нормального распределения с нулевым средним и единичной дисперсией. На рис.1.7 приведена выборочная АКФ этого ряда, рассчитанная до лага, равного 15 временным единицам. На этом рисунке в первом, втором и третьем столбцах слева от поля диаграмм приведены, соответственно, величины лагов, значения АКФ и ее ошибки; в первом и втором столбцах справа - значения критерия Бокса-Льюинга (тест на случайность) и уровень значимости. Значения АКФ находятся в пределах доверительного интервала, поэтому можно сделать вывод о независимости соседних значений приведенного ВР.
Рис.1.6. 100 смоделированных значений
Рис.1.7. Выборочная автокорреляционная функция
Введем понятие белого шума, под которым подразумевается ВР, компонентыкоторого { Х t } представляют собой последовательность независимых и идентично распределенных СВ с конечными средним и дисперсией. В частности, если Х t - нормально распределены с нулевым средним и дисперсией σ2, то такой ряд называется гауссовым белым шумом (white noise), для которого можно записать
{ Х t } ~ WN (0, σ2).
Концепция белого шума широко используется при построении моделей ВР. Например, семейство классических процессов ARMA, о которых будем говорить ниже, формируется из «строительных блоков», представляющих собой белый шум.
Для ряда, который является белым шумом, все АКФ равны нулю вследствие независимости СВ. В практических задачах, когда выборочные значения АКФ какого-либо ряда близки к нулю, считается, что анализируемый ряд есть белый шум.
Временной ряд является линейным процессом, если его можно представить следующим образом
(1.1)
где μ - математическое ожидание Xt; at - белый шум.
Соотношение (1.1) представляет собой теорему Вольда, из которой следует, что всякий процесс может быть выражен в виде линейной комбинации значений белого шума с разными весовыми коэффициентами ψ i. Волд доказал, что стационарный процесс, который является чисто недетерминированным (рurely non-deterministic) всегда может быть представлен в виде (1.1).
Для линейного ВР, описываемого равенством (1.1), динамическая структура процесса Xt управляется посредством весовых коэффициентов. Если Xt - слабо стационарный ряд, можно получить его среднее и дисперсию, используя независимость { at }, в виде
где σ a 2 - дисперсия at.
Кроме того, автоковариация процесса Xt при лаге, равном l, определяется следующим образом
Следовательно, веса ψ i связаны с автокорреляциями процесса Xt соотношением
(1.2)
Для того чтобы выражение (1.1) имело смысл, необходимо потребовать выполнения условия сходимости по вероятности, так как суммируются случайные величины. Это условие записывается в виде
Поскольку реализации белого шума не наблюдаемы, можно считать, что весовые коэффициенты определены с точностью до множителя. При этом значение ψ0 принимается равным единице, что и установлено в равенстве (1.2).
Чем больше весовой коэффициент ψ l, тем больше влияние случайного возмущения в момент t – l на текущий момент t. Конечно, бесконечное число слагаемых в выражении (1.1) приводит к значительным проблемам вычислительного характера, но оказалось, что во многих практических ситуациях достаточно рассматривать частные случаи представления Вольда, когда число слагаемых - конечно.
Кроме рассмотренной выше АКФ между Х t и Х t + h, обратимся к анализу корреляции между этими же значениями после того, как совместное линейное влияние на промежуточные значения Х t + 1, Х t + 2, ..., Х t + h -1 будет устранено. Условная корреляция Corr (Х t, Х t + h | Х t + 1,..., Х t + h -1) называется частной автокорреляционной функцией (ЧАКФ) в задачах анализа ВР.
ЧАКФ ряда является функцией его АКФ. Отметим, что АКФ определяется ковариацией между значениями процесса, отстоящими на h шагов по времени друг от друга. Однако на поведение процесса статистически влияет не только его значение в момент, равный τ шагов назад, но и все промежуточные значения процесса между моментами t и t – h. ЧАКФ исключает влияние всех промежуточных значений ряда и показывает лишь "чистую" взаимосвязь между моментами t и t – h.
Частная автокорреляция может быть выведена следующим образом. Рассмотрим регрессионную модель, в которой зависимая переменная Х t + k, взятая из стационарного процесса с нулевым средним, регрессирует на k задержанных переменных Х t + k - 1, Х t + k - 2,..., Х t, т.е.
(1.3)
где 
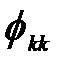- коэффициенты регрессионного уравнения; 
- помеха в уравнении регрессии.
Умножив обе стороны уравнения (1.3) на величину Х t + k - j и определив математическое ожидание, получим
следовательно,
(1.4)
Для j = 1, 2,..., k имеем следующую систему уравнений
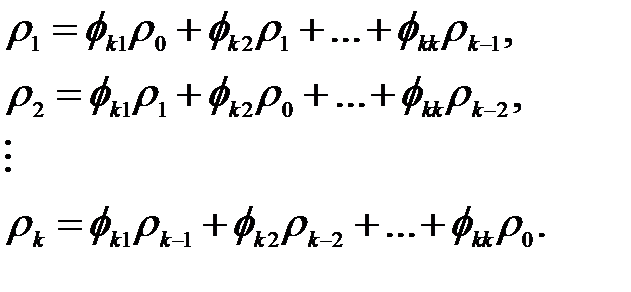
Последовательно используя правило Крамера для k = 1, 2, …, имеем
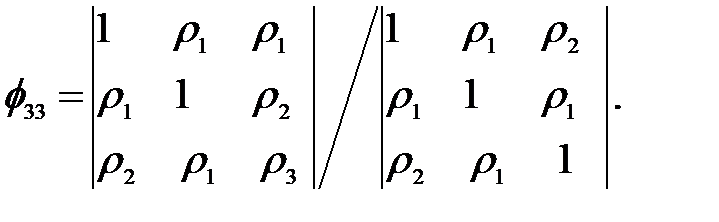…(1.5)
Таким образом, значения 
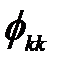определяют ЧАКФ на разных лагах. В итоге, частная автокорреляция между Х t и Х t + k определяется коэффициентами уравнения регрессии, связывающего переменную Х t + k с k задержанными переменными Х t + k - 1, Х t + k - 2,..., Х t. Отметим, что алгебраическое вычисление ЧАКФ представляет собой достаточно трудоемкий процесс, поэтому в большинстве прикладных пакетов ее определение проводится численным образом с использованием стандартных программ. В качестве иллюстрации на рис.1.8 приведена выборочная ЧАКФ для данных, использованных в примере 1.1.
Рис.1.8 Выборочная частная автокорреляционная функция
