В случае присутствия диссипации в линии G и R ≠ 0. Будем по-прежнему записывать
напряжение и ток виде:
Подставляя эти выражения в телеграфные уравнения (8.1 и 8.2), получаем уравнения:
так как экспоненты сократились. (8.14)
(8.15)
Это уравнение Гельмгольца. (8.16)
Здесь (8.17)
Коэффициент γ носит название постоянной распространения. Действительная часть постоянной распространения α характеризует изменение амплитуды сигнала на единицу расстояния и носит название коэффициента затухания.
Мнимая часть β(ω) характеризует изменение фазы на единицу расстояния и носит название фазовой постоянной. Фазовая постоянная, зависящая от частоты, является аналогом волнового числа k в бездиссипативной линии.
Решением уравнения (8.16) является функция вида
(8.18)
Если то бегущая вправо волна запишется в виде:
(8.19)
Выражение (8.18) описывает встречные бегущие волны. Наблюдатель в фиксированной точке x = const видит периодические колебания напряжения во времени, а «мгновенный снимок» в момент t = const показывает периодическое изменение U вдоль пространственной переменной.
Условие постоянства фазы прямой волны (8.19) имеет вид (ωt – β x) = const. Дифференцируя это соотношение по времени, получаем
или
Скорость cph является фазовой скоростью: двигаясь в направлении распространения волны с этой скоростью наблюдатель будет видеть постоянную фазу бегущей волны. Поскольку фазовая постоянная зависит от частоты β = β(ω), в реальной линии с диссипацией имеет место дисперсия скорости cph = cph (ω).
Из (8.15) или
Из (8.18) Отсюда
(8.20)
Для волны, бегущей вправо, поделим напряжение (8.18) на ток (8.20) и получим волновое сопротивление линии с диссипацией:
(8.21)
Для волны, бегущей влево, знак тока поменяется.
Подытожим основные отличия реальной линии с диссипацией от идеальной линии без потерь. В реальной линии сигналы затухают с расстоянием, причём степень ослабления зависит от частоты α = α(ω). В линии с потерями имеет место дисперсия скорости распространения сигнала, то есть cph = cph (ω). Согласование реальной линии с нагрузкой требует учёта частотной зависимости волнового сопротивления ρ = ρ (ω). Дисперсия коэффициента затухания и фазовой скорости сигнала, а также волнового сопротивления линии приводит к искажению формы сложных (негармонических) сигналов.
Линия с малыми потерями
На практике часто активные потери в линии малы по сравнению с реактивными составляющими, то есть выполняются условия G << ωC и R << ωL. Получим выражения для коэффициента затухания в этом случае.
Запишем постоянную распространения (8.17) в виде
(8.22)
В произведении под корнем пренебрежём членами второго порядка малости и разложим подкоренное выражение в ряд, ограничиваясь первыми членами разложения:
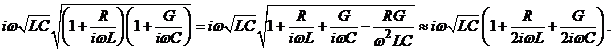
(8.23)
Искажение формы становится особенно серьёзной проблемой при передаче коротких импульсов, имеющих широкий частотный спектр. Хевисайдом были сформулированы условия, позволяющие построить неискажающую передающую линию:
(8.24)
Покажем, что при выполнении этого соотношения коэффициент затухания, фазовая скорость и волновое сопротивление становятся частотно-независимыми. Обозначим
и подставим в (8.23). Получится
В этом случае получаем коэффициент затухания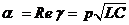 
, (8.25)
фазовую постоянную 
(8.26)
и волновое сопротивление
(8.27)
Таким образом, выполнение условия Хевисайда (8.24) исключает искажения формы сигнала, поскольку все частотные составляющие сложного сигнала ослабляются в равной мере и перемещаются с одинаковой скоростью 
, равной фазовой скорости в идеальной линии. На приёмном конце линии получается копия отправленного сигнала, уменьшенная по амплитуде в αL раз. Волновое сопротивление неискажающей линии совпадает с волновым сопротивлением идеальной линии без потерь.
Приложения
Оливер Лодж
Изобретатель радио сэр Оливер Джозеф Лодж (Sir Oliver Joseph Lodge) родился 12 июня 1851 г. в городке Пенкхалл (Penkhull). Получил степень бакалавра (1875) и доктора (1877) Лондонского университета. С 1881 – профессор физики и математики в Университетском колледже Ливерпуля. С 1900 – директор вновь открытого Бирмингемского университета. В 1902 г. произведён в рыцари. В 1919 г. вышел на пенсию.
14 августа 1894 г. на заседании Британской ассоциации содействия развитию науки в Оксфордском университете Лодж произвёл первую успешную демонстрацию радиотелеграфии. В ходе демонстрации радиосигнал азбуки Морзе был отправлен из лаборатории в соседнем Кларендоновском корпусе и принят аппаратом на расстоянии 40 м – в театре Музея естественной истории, где проходила лекция. Лекция была посвящена памяти Генриха Герца, скончавшегося 1 января 1894 г.
Лодж использовал трубку Бранли, но назвал её "когерером" – "сцеплятелем". Заслугой Лоджа было то, что он приспособил когерер к исследованию волн Герца, заметив: "Когерер удивительно чувствителен к волнам Герца". Неприятному свойству порошков не расклеиваться Лодж противопоставил механизм; через определённые промежутки времени трубка встряхивалась.
Вот что сказал А.С.Попов в своём докладе "Телеграфия без проводов", прочитанном 29 декабря 1899 г. на соединённом заседании русского технического общества и Первого Всероссийского электротехнического съезда и опубликованном в "Физико-математическом ежегоднике" 1900, №1, с.100-121: "В первый раз телеграфный аппарат при помощи трубки Бранли был приведён в действие Лоджем. Трубка была включена последовательно с электромагнитом телеграфа и батареей. Волна, произведённая разрядом, происшедшим по соседству, замыкала ток и якорь притягивался, но ненадолго, потому что трубка постоянно встряхивалась особой зацепкой, на одной из быстро вращающихся осей телеграфного аппарата, выходящей наружу". http:// www. oldradioclub. ru / raznoe / hystory / hystory _041. html
Много лет спустя Лодж сам говорил об этом периоде его работы так: "Хотя метод сигнализации на небольшом расстоянии через стены или другие непроводящие тела посредством волн Герца, посылаемых одной станцией и обнаруживаемых трубкой Бранли на другой станции, применялся автором и некоторыми другими авторами в Англии, он не был использован ими для практического телеграфирования. Идея замены гальванометра на реле, работающее как звукоуказатель, или телеграфным аппаратом Морзе сама по себе очевидна, но была столь далека от интересов автора в то время, что он не увидел, какой бы то ни было практической возможности телеграфирования через пространство... В этом заблуждении относительно практических применений беспроволочной телеграфии он, несомненно, ошибался. Другие не были столь слепы, хотя и не менее автора заняты".
О. Lodge. Signalling across space without wires, being a description of "Work of Hertz and his successors". 4 ed. London, 1901, p. 45.
