Пусть, например, две измеряемые величины, x и y, связаны между собой линейной зависимостью:
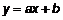 ,
,
где a и b – неизвестные параметры. Результатом экспериментальных измерений является несколько пар значений xi и yi (i = 1,2,… n, где n – количество измерений). Поскольку величины xi и yi измерены с некоторой погрешностью, то экспериментальные точки не ложатся на одну прямую (рис. 5).
В этом случае «наилучшей» прямой будет та, для которой сумма квадратов расстояний от точек до неё будет минимальной. На основе этого критерия можно получить выражения для параметров a и b:
 , (16)
, (16)
 , (17)
, (17)
а также оценки для погрешностей этих величин:
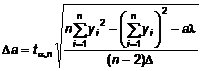 , (18)
, (18)
 , (19)
, (19)
где
 ,
,
 .
.
Возможность использования метода наименьших квадратов при нелинейной зависимости измеряемых величин обусловлена тем, что в ряде случаев такие зависимости можно свести к линейным путём замены переменой; например, для функции y = ln ax можно строить график зависимости y от ln x (y = ln x + ln a).
Применение метода наименьших квадратов для обработки результатов измерений эффективно при использовании программируемых калькуляторов или компьютеров с соответствующим программным обеспечением, например, достаточно широко распространённой программой Microsoft Excel из пакета Microsoft Office, а также специализированными программами MathCAD, Matematica, MAPL и т.п.
Ещё раз необходимо подчеркнуть, что применение метода наименьших квадратов возможно только при известном виде функциональной зависимости измеряемых величин. В противном случае результаты расчётов могут потерять физический смысл.
7. Использование программы Microsoft Excel для обработки экспериментальных данных.
В состав Microsoft Excel входит весьма большой набор средств анализа данных (так называемый пакет анализа), предназначенный для выполнения сложных статистических и инженерных расчётов. Кроме того, Excel имеет удобные инструменты для оформления результатов в графическом виде. Подробное описание работы с этой программой выходит за рамки данного пособия. Приведём лишь несколько полезных советов и рекомендаций.
1. Для расчёта погрешности прямых измерений следует воспользоваться инструментом описательная статистика. При этом стандартная ошибка в программе вычисляется по формуле (2), т.е. без учёта коэффициента Стьюдента.
2. Для построения графиков следует выбрать точечную диаграмму. Если предполагается производить статистическую обработку данных, то желательно выбрать точечную диаграмму без соединительных линий.
3. При использовании метода наименьших квадратов следует внимательно выбирать линию тренда; она должна соответствовать имеющейся (или ожидаемой) функциональной зависимости.
4. Следует уделить внимание оформлению графика, т.е. ввести названия осей, размерности величин, масштабы по осям. Желательно также отобразить доверительные интервалы на экспериментальных точках.
Литература
1. Руководство к лабораторным занятиям по физике. Под ред. Л.Л. Гольдина. – М.: Наука, 1973.
2. Основы математической обработки результатов измерений. Методические указания. – Изд. ТюмГУ, Тюмень, 1986.
3. Лабораторный практикум по физике. Под ред. К.А.Барсукова и Ю.И. Уханова. – М.: Высшая школа, 1988.
4. Физический эксперимент. Методические указания. – Изд. ТюмГУ, Тюмень, 1994.
Дополнительная Литература
5. Яноши Л. Теория и практика обработки результатов измерений: Пер. с англ. – М.: Мир, 1968.
6. Squires G.L. Practical Physics. – McGraw-Hill, London, 1976.
7. Preston J.W. Experiments in Physics. – John Wiley, N.Y., 1985.
8. Смирнов Н.В., Белугин Д.А. Теория вероятностей и математическая статистика в приложении к геодезии. – М.: Недра, 1969.
Физический практикум
Учебно-методические рекомендации
для студентов физического факультета
Безуглый Борис Антонович
Монтанари Сергей Георгиевич
Печать офсетная
Подписано в печать _________________ Заказ №_____________
Объем __________ п.л. Тираж _________________ экз.
Издательство Тюменского государственного университета
625003, г. Тюмень, ул. Семакова, 10






