Пусть для косвенных измерений физической величины А используется известная функциональная зависимость А от ряда других независимых величин x, y, z, b, c, d,..., q, заданная в форме A = f (x, y, z, b, c, d..., q). Среди переменных могут быть величины трех типов:
1) Величины, определяемые путем прямых измерений (например, величины x, y, z), которые после проведения этих измерений представляются в стандартной форме:
x = 
± D x; y = 
± D y; z =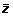 
± D z.
2) Данные установки (например, величины b и c), т.е. характеристики экспериментальной установки, известные из предыдущих измерений. Эти величины также должны быть заданы в аналогичной форме:
b =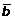 
± D b; c = 
± D c.
В противном случае считают, что погрешность равна половине последней значащей цифры.
3) Табличные величины (например, величина d) - величины, которые в данном опыте не измеряются, а берутся из таблиц. Табличная величина может быть константой (например, d = p). В этом случае её нужно брать с такой точностью, чтобы относительная погрешность была значительно меньше относительных погрешностей всех остальных величин, входящих в функциональное выражение величины А. Если же d - заданная в табличной форме функция непосредственно измеряемой величины, то ее также нужно представить в стандартной форме:
d = 
± D d.
Наилучшим значением величины А при косвенном её измерении будет
.
Правила расчета погрешностей косвенных измерений.
1. При вычислении погрешностей косвенных измерений:
1) складываются не модули, а квадраты погрешностей, обусловленных независимыми источниками;
2) погрешности, даваемые различными источниками, необходимо вычислять раздельно и обязательно учитывать максимальный вклад в погрешность окончательного результата; рекомендуется отбрасывать те погрешности, которые хотя бы вдвое меньше максимальной.
2. Стандартная погрешность величины A принимается равной:
, (12)
где 
, 
,.... 
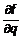- частные производные функции f, вычисляемые при подстановке средних значений соответствующих переменных.
В некоторых случаях удобнее воспользоваться выражением для относительной погрешности 
:
, (13)
поскольку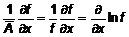 
и так далее.
Выражение (13) удобно использовать в том случае, когда расчётная формула содержит только действия умножения и деления.
Таким образом, для вычисления погрешности косвенных измерений необходимо выполнить следующие операции:
1) Для каждой серии измерений физических величин произвести обработку результатов прямых измерений. При этом для всех измерений должно быть задано одно и то же значение доверительной вероятности.
2) Найти частные производные функции f (или ln f) и их численные значения, после чего определить погрешность D А.
3) Записать результат измерения в стандартной форме:
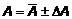, (a) (14)
или, используя относительную погрешность,
, (a). (15)
