Мақсаты: Идеал газ дегеніміз не екенін, идеал газ заңдары мен изопроцестерді студенттерге жетік түсіндіру.
Жоспары:
1. Идеал газ заңдары (Бойль-Мариотт заңы, Шарль заңы, Гей Люссак заңы).
2. Менделеев-Клапейрон заңы.
Негізгі ұғымдары: идеал газ, изотермиялық процесс, изобаралық процесс, изохоралық процесс, парциал қысымдар.
Идеал газ деп молекулалар арасында өзара әсерлесу күштрі болмайтын, жеке молекулалар көлемі ыдыс көлемімен салыстырғанда өте аз және малекулалар арасындағы өзара соқтығысуы абсолют серпімді болатын газды айтады. Көптеген тәжірибелер бойынша қалыпты жағдайда (оттек,гелий), яғни төменгі қысымда және жоғарғы температурада нақты газдар қасиеті идел газ қасиетіне сәйкес келеді.
Молекула-кинетикалық теория ашылғанға дейін идеал газдар қасиетін сипаттайтын көптеген заңдылықтар болған.
Бойль-Мариотт заңы. Газ күйіндегі заттардың меншікті көлемі болмайды. Сондықтан газдар ыдысқа толтырылғанда, сол ыдыстың көлемін толық алып тұрады және ыдыс қабырғаларына белгілі бір қысым күшін түсіреді. XVII ғасырдың ортасында ағылшын ғалымы Р.Бойль (1627-1691) және француз физигі З.Мариотт (1620-1684) бір-біріне тәуелсіз жасалған тәжірибе қорытындыларынан, температура тұрақты болғанда газ көлемінің (v) оның қысымына (p) тәуелді өзгеретінің тұжырымдады, яғни берілген газ массасы үшін тұрақты температурада оның қысымы көлеміне кері пропорционал өзгереді, яғни
PV= const, 
= 
(1)
Бұл тәуелділікті изотерма деп аталатын гипербола қисығымен көрсетуге болады.(1-сурет)
Р 
V (1-сурет)
Газ күйінің бір күйден екінші күйге тұрақты температурада өтуі изотермиялық процес деп аталады. Ал нақты газдар бұл заңдылыққа тек тығыздықтары өте аз болғанда ғана бағынады. Сонымен,тұрақты температурада Р мен V тәуелділігі заттар қасиетін сипаттайды.
Гей-Люссак заңы. Газ көлемінің (V) оның температурасына (Т) тұрақты қысымда (р=const) тәуелді болу шартын бірінші рет француз ғалымы Гей-Люссак (1778-1850) тағайындады: берілген газ массасы үшін қысымы тұрақты болғанда, газ көлемі оның температурасына сызықты тәуелді өзгереді (p=const, m=const)
, (2)
Мұндағы 
– газдың 
– тағы көлемі, 
– газдың көлемдік ұлғаюының термиялық коэффициенті. Тұрақтық қысымда газ көлемі мен температура тәуелділігі гракфикте түзу сызықпен көрсетіледі. Қысымның әрбір мәніне сәйкес келетін түзу сызық изобара деп аталады. Ал газ күйінің тұрақты қысымда өзгеруі изобаралық процесс делінеді.
Шарль заңы. Тұрақты көлемде газ температурасының қысымға тәуелді болатыны да анықталады,яғни белгілі газдың массасы үшін көлемі тұрақты болғанда, газ қысымы оның температурасына сызықты тәуелділікке өзгеріледі(V=const. m=const)
(3)
мұндағы 
- газдың – тағы қысымы, 
- газ қысымының термиялық коэффициенті. Көлем тұрақты болғанда, 
мен t тәуелділігі түзу сызықты және ол изохора деп аталады(3-сурет). Газ күйінің мұндай өзгеруі изохоралық процесс дейді. Зерттеудің нәтижелері газдардың термиялық коэффициенттері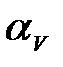 
және бір-біріне шамалас екенін көрсетеді, яғни
Изобара және изохора түзулері абсцисса өсінде шамасы 
нүктесінде қиылысады. Температурасыны бастапқы санау нүктесін осы нүктеге ауыстырып, температурасының Цельсии шкаласынан абсолют кельвин шкаласы деп аталатын басқа температуралық шкалаға өтуге болады.
Бірліктердің халық аралық жүйесінде Кельвин – температурасының термодинамикалық шкаласында негізгі өлшем болып, су күйінің үштік нүктесіне сәкес келетін термодинамикалық температураның I/273,15 нлесіне тең болады. Абсолют температура Т мен Цельсии бойынша анықталған t температурасының арасында мынандай қатынас болады.
Мысалы, -қа + 273,15 К сәкес келеді. 
–қа тең температура абсолют нөл деп аталады, оған 
мәні сәйкес келеді.
Енді (2) және (3) теңдеулерге абсолют температураның мәнің қойып, оны басқа түрде жазуға болады
немесе 
Бұдан 
.Егер 
мен 
тұрақты шама екенін ескерсек, онда изобаралық процесс үшін: 
. (4)
Осындай әдіспен изохоралық процесс үшін де мынадай теңдікті жазуға болды, яғни 
(5)
Авогадро тағайындаған заң бойынша бірдей жағдайларда, яғни бірдей температура мен қысымда барлық газдардың модельдерінің көлемі бірдей болады. Қалыпты жағдайда: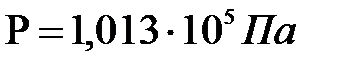 
; Т=273,15К болса, оның көлемі 
тең
Әр түрлі заттарындың бір мольдегі молекулалар саны бірдей болады: 
, бұл Авагадро саны деп аталады.
Ағылшын физигі және химигі Дж.Дальтон (1766-1844) тағайыңдаған заң бойынша, идеал газдар қоспасының жалпы қысымы,сол қоспаны құрайтын газдардың парциал қысымдарының қосындысына тең болады, яғни
= 
+ 
+ 
+ 
+ 
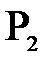(6)
Мұндағы + 
+ 
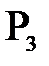+ + -парциал қысымдар.
Сонымен идеал газдың берілген массасы үшін (m=const) жоғарыда қарастырылған заңдылықтар, яғни: 
=const (изотермиялық процесс), 
=const (изобаралық процесс), P/T=const (изохоралық процесс) дұрыс екен.
Массасы m газдың алғашқы күйін сипаттайтынпараметрлердің мәндері P 
, , 
болсын.Егер газдыңкүйі өзгерсе,онда оның соңғы күйін сипаттайтын параметрлер 
, 
, 
болады. Бойль-Мариотт және Гей-Люссак заңдары негізінде осы газдың екі күйінің арасындағы байланысты анықтауға болады.Ол үшін газдың бірінші күйдегі қысымын тұрақты деп (P 
= const), оны -ден -ге дейін қыздырамыз. Сонда оның көлемі -ден 
ке дейін өзгереді. Бұл процесс изобаралық болғандықтан, Гей-Люссак заңы бойынша көлемнің өзгеруі: 
. Енді газ күйінің соңғы өзгерісін тұрақты температурада (Т= const), оның көлемін өзгертіп байқауға болады: яғни газ қысымы 
-дан 
-ге дейін өзгерсе, көлемі 
-ден -ге ұлғаяды. Бұл өзгеріс изотермиялық болғандықтан, Бойль-Мариотт заңы негізінде
Бұл екі қатынастың сол жақтары өзара тең болғандықтан:
( / 
)= (
/ 
).
Осы теңдіктің екі жағын да 
көбейтіп, бөлсек
(
)/ =(
)/ .
Сонымен,берілген газ массасы үшін, газ күйінің өзгерісін көзсететін шама (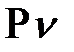
)/Т әр уақытта тұрақты болады екен, яғни
(
)/Т= const. (7)
Бұл теңдікті бірінші рет француз физигі және инженері С.Клапейрон (1799-1864) Бойль-Мариотт және Гей-Люссак заңдарын біріктіріп, қорытып шығарғандықтан, ол идеал газ күйін сипаттайтын Клапейрон теңдеуі деп аталады.
Қалыпты жағдайда, яғни температура (0 
С) және атмосфералық қысым (
=1,01*10 
Па) болса, онда кез келген газдың бір молінің көлем 
болады. Сондықтан газдың сандық мәні бір мольге тең болса,(7) теңдіктерге тұрақты шама барлық газдар үшін бірдей болады. Барлық газ үшін тұрақты шаманы R әріпімен белгілеп, оны универсал газ тұрақтысы деп атайды. Сонда (7) теңдік мына түрде жазылады:
= RТ. (8)
Енді (8)теңдеуден универсал газ тұрақтысының сандық мәнін анықтап шығарайық. Егер Т=273К, 
, 
, Онда
R= 
=8,31 Дж/(моль·К).
1 мольге ғана дұрыс болатын 
=RT (
= 
) формуланы кез келген мөлшердегі массаға қолданатындай өзгертіп жазуға болады. Ол үшін газдың молярлық массасын 
әріпімен белгілейміз. Олай болса, тұрақты қысым мен температурада
(
=const), 
; 
(9)
Бұл теңдік массасы m кез келген газ үшін ұорытылып шығарылған Клапейрон-Менделеев теңдеуі болып табылады.
Универсал газ тұрақтысының физикалық мәнін түсіндірейік. Жеңіл қозғалатын поршені бар цилиндрлі ыдыста көлемі 1 моль газ болсын (4-сурет). Газ жылжымалы поршеньге сыртқы қысымға тең P=const қысым түсіреді. Цилиндр ішіндегі газды 1К температураға қыздырса, оның көлемі ұлғайып, поршеньді h биіктікке көтереді. Поршеньге түсіретін қысым
Мұндағы F-поршеньге түсірілетін қысым күші, S- поршеньнің ауданы. Сонда қысым күші: 
. Газдың поршеньді h биіктікке көтергенде істейтін сыртқы жұмысы 
,мұндағы Sh көбейтіндісі газ көлемінің өсімшесін көрсетеді, яғни 
,сонда газ көлемінің ұлғаю кезіндегі жұмыс
(10)
Егер газдың алғашқы күйін сипаттайтын теңдеу
(11)
болса, 1К қыздырғаннан кейінгі көлемі 
=ге өзгеріп, (11) теңдеу басқа түрде көрсетіледі, яғни
(12)
Соңғы (11) және (12) теңдеулерден мына теңдік шығады
(13)
Егер де (10) және (13) теңдеулерді салыстырсақ, онда универсал газ тұрақтысы істелген жұмысқа тең болады:
A=R (14)
Сонымен, универсал газ тұрақтысы 1 моль газды 1К температураға қыздыру үшін кеткен изобаралық жұмысқа тең екен.
Қорыта келе: Заңдылықпен құқық тәртібін қорғаштау, адамның құқығы мен бостандығын қорғау, қылмыспен және басқа да құқық бұзушылықтармен күресу негізгі (арнайы) міндеті болып табылатын мемлекеттік органдар.
Криминалистика на: сот, төрелік сот, конституциялық сот, прокуратура, ішкі істер, ұлттық қауіпсіздік, әділет, төрелік, кедендік бақылау, қаржы полициясы органдары және т.б. жатады.
Криминалистика – заңдылықты және құқық тәртібін, адам құқықтары мен бостандықтарын қорғау және қылмысқа қарсы күрес міндеттерін атқаратын мемлекеттік органдар. Криминалистика на сот, төрелік сот, Конституциялық сот (Қазақстанда Конституц. кеңес), прокуратура, ішкі істер органдары, мемлекеттік қауіпсіздік (Қазақстанда өлттық қауіпсіздік), кедендік бақылау, әділет органдары жатады. Кең мағынада алғанда, Криминалистика ұғымы бірқатар беймемл. институттарды да: адвокатураны, аралық сотты, т.б. қамтиды. Күшейтілген қылмыстық-құқықтық қорғау жүйесіне қауіпсіздік шаралары мен әлеум. шаралар да кіреді
Өзін-өзі бақылау сұрақтары:
1. Молекулалық қозғалыстың кинематикалық сипаттамалары.
2. Термометрикалық дене және термометрикалық шама.
Негізгі және қосымша әдебиеттер тізімі:
1. Матвеев А.Н. Молекулярная физика. – Высш.шк., 1987. – 360 с.
2. Абдулаев Ж. Физика курсы: Жоғары оқу орын.студ.арналған оқулық /Ж. Абдулаев, П. Аскаров.- Алматы: Ғылым, 2004.
3. Құлбекұлы.М. Молекулалық физика және термодинамика: Оқу құралы.- Алматы: Қарасай, 2005-248бет.
Дәріс тақырыбы. Математикалық статистиканың негізгі ұғымдары. Молекулалық жүйедегі кездейсоқ оқиғалар мен кездейсоқ шамалар.
Дәрістің мақсаты: Математикалық статистиканың негізгі ұғымдары түсіндіру.
Дәрістің жоспары:
1. Математикалық статистиканың негізгі ұғымдары
2. Молекулалық жүйедегі кездейсоқ оқиғалар мен кездейсоқ шамалар
Молекулалық физиканың көзқарасы бойынша әрбір зат орасан сан кішкентай бөлшектерден тұрады.Олар үздіксіз қозғалады және осы қозғалыс кезінде бір-біріне әсер етеді.Бірақ бұл бөлшектердің жаратылысы, олардыңарасында болатын әрекеттесулер мен қозғалыс сипаттары және тағы басқа қасиеттері туралы белгілі мәліметтер жеткіліксіз. Жалпы алғанда, бұл мағлұматтар заттың құрамындағы бөлшектер өте көп және біртекті жүйеде олардың қасиеттері үйлес деп қарауға мүмкіндік тудырады.
Бөлшектерді Ньютонның механикасы заңымен қозғалады десек, онда N молекуланың әрқайсысының қозғалыс теңдеуі былай жазылады.
мұндағы moi – I молекуланың массасы, vi - I молекуланың жылдамдығы, Fik- I және k – молекуланың өзара әрекеттесу күші, i= 1,2,3,….N.
Бұл дифференциалдық теңдеуді қолдану үшін заттың құрамындағы молекулалардың құрлымы және өзары әрекеттесу заңдары белгілі болуы қажет. Тіпті айтылған қиыншылықтар болмасын, онда (3.1) – ші теңдеуді интегралдау әр молекуланың қозғалысын сипаттайтын орасан теңдеулер жүйесін шешуді талап етеді. Ескере кетейік, қалыпты жағдайда 1м3 газда 2,7 1025 молекула болады.
Сондықтан әр молекуланың алғашқы хi, уi, zi координаттары мен алғашқы vix viу viz жылдамдықтар проекциясын білу және олардың траекториясын табу мүмкін емес. Бұл тұрғыдан алғанда, жеке молекулалардың траекториясы мен қозғалыс заңын анықтауға мүмкіндік туса да, ол бізге тұтас газдың қасиеттері туралы ешқандай мәліметтер бере алмайды.
Шынында, мұндағы туындайтын мәселе жеке молекулалардың қозғалысына назар аудармай, тек бөлшектердің орасан зор жиынтығының және әрекеттесуін сипаттайтын заңдылықтарын ғана пайдаланады.Осы айтылған заңдылықтардың өзіне тән ерекшеліктер бар және олар қозғалыстардың қарапайым қосындысымен анықталмайды.
Қисапсыз сан бөлшектерден тұратын жүйеде, жаңа, көпшілікке бірдеилік, таза статистикалық немесе ықтималдық заңдылықтар пайда болды. Бөлшектер саны аз жүйеде мұндай заңдылықтар болмайды.Сондықтан, көпсанды бөлшектердің әрекеттесуі себепші болатын құбылыстарды зерттегенде, жеке молекуланың қасиеттерін ескерудің қажеті болмайды.
Көпшілікке қатысты кездейсоқ оқиғалардың заңдылықтары ықтималдық теорияның ұғымдарымен негізделеді.
Сондықтан, статистикалық әдіс заттың микроскоптық массасынан өтетін құбылыстардың заңдарын жеке бөлшектердің қозғалысын басқаратын заңдары арқылы тағайындайды. Демек, статистикалық әдіс заттағы байқалатын құбылыстардың заңдарын, оның атомдық- молекулалық құрлымына сүйеніп зерттейді.
Ықтималдық теорияның негізгі ұғымының біреуі кездейсоқ шама деген болады. Мысалы, газдың молекуласының жылдамдығы тұрақты болмайды, неге десе, басқа молекуламен соқтығысуына байланысты өзгереді. Мұндай соқтығысулар аз уақыт аралығында өте көп. Белгілі уақытта молекуланың жылдамдығын білсек те, біз оның дәл мәнін 0,01 немесе 0,001 секунд өткенде неге тең екенін анықтай аламыз. Тіпті жеке молекуланың өзін орасан жиынтық ішінде белгілеуіміз де мүмкін емес. Молекуланың жылдамдығының өзгерісі кездейсоқ сипатқа ие, демек кездейсоқ шамаға жатады. Әр жеке молекулақандай жылдамдықпен қозғалады және тап осы кезде қай жерде ьолатынын алдын ала болжау мүмкін емес, өйткені олар кездейсоқ шамалар.
Мысалы, су буға айналады(бұны А оқиға десек), оны отмосфералық қысымда 100ос температурада қыздырсақ (қыздыру А оқиғаның болу шарты). Демек, әр G шарттар комплексі(жиынтығы) іске асырылса, А оқиға болады.
Әр G комплекс шарттары жүзеге асырыағанда сөзсіз болатын оқйғаны аққиқатты деп атайды.
Оқиға мүмкін емес, егер оның болмайтынын біле тұра G комплекске шарттары жүзеге асырылғанда, оның болуы да, болмауы да мүмкін.
Оқиғаның ақиқаттығы, мүмкін еместігі, кездейсоқтығы белгілі G шарттар комплексіне қатысты анықталады.
Молекулалық қозғалыстың және осы қозғалыс температураға тәуелділігінің негізгі көрнекі дәлелдігі броуындық қозғалыс болады. Сұйықтың немесе газдың ішінде қалқыған молекулалардың соққылау әсерінен туындаған кішкентай бөлшектердің ретсіз хаосты қозғалысы броуындық қозғалыс деп аталады. Ағылшын ботанигі Р. Броун 1827 ж. байқаған бұл құбылыста суға салынған гүлдің аталығы (өте кішкене тұқымдары) бейберекет қозғалып, өзінің қозғалыс бағытын өзгертеді.
Бөлшектердің траекториясы күрделі ирек-ирек, қозғалыс қарқындылығы уақытқа тәуелсіз бірақ ортаның температурасы көтерілгенде өседі. Ортаның молекулаларының соққылары қалқығанбөлшекті ретсіз қозғалысқа түсіреді: оның жылдамдығының бағыты және шамасы тез өзгеріп отырады. Сондықтан бөлшектердің траекториясы өте күрделі және шиеленісіп кеткен.
Қалқыған бөлшекке ортаның молекулалары әсер ететін еүштің бағыты молекулалары әсер ететін күшті бағыты үздіксіз өзгереді, одан бөлшектердің ығысуының проекциясының орташа квадраты 
бақылаудың t уақытына пропорционал болады:
мұндағы D-броундық бөлшектің диффузия коэффиеценті.
Бұл теңдеуді Эйнштейн заңы деп атайды. Бұл қатынас Ж.Перрен мен Т. Сведбергтің эксперементтік зерттеулерінің нәтижелерін арқылы дәлелденген. Олардың өлшеулерінің нәтижелері арқылы дәлелденген. Олардың өлшеулерінің нәтижелері арқалы k-Больцман тұрақтысы мен NA Авогадро саны анықталған.
Броундық қозғалыстағы молекулалардың координаттары, жылдамдықтары мен импульстерінің мәндері кездейсоқ шамалар ретінде қарастырылады. Броундық қозғалыстың теориясы сұйықтағы бөлшектің қозғалысын сол ортаның молекулаларының соққылау әсеріне туындаған кездеисоқ қозғалыстың теңдеуін шешу арқылы тағайындайды. Броундық қозғалыстың математикалық моделі арнайы статистикалық физика курсында қаралады.
Статистикалық зерттеудің мақсаты орасан көп бөлшектерден құралатын жүйенің микроскоптық қасиеттерін бейнелеу мен түсіндіру. Сондықтан статистикалық әдістің негізгі нәтижесі термодинамиканың шамаларының статистикалық мәнін ұғынуды көздеиді.
Жоғарыда айтылғандардан, газ молекулаларының кезектегі қозғалысын бақылаумен қатар, олардың белгілі уақыттағы орны мен қозғалыс күйін анықтау қиын мәселе. Сол себептен біз газдың тек статистикалық қасиеттеріне көңіл аударамыз. Ол қасиеттерге мыналар жатады: көлем элементіндегі молекулалардың орташа саны, импульс, немесе өте аз уақыт интервал бойынша орташаланған энэргиясы, немесе басқа қозғалыс сипаттарының орташа үйлестірулері және басқа қозғалыс сипаттарының орташа үйлестірулері.
Бұндай шек қойылуда тек матаматикалық себептерден деп ұғынуға болмайды. Себебі эксперементте газдың белгілі массасының тек орташаланған қасиеттері өлшенетін болғандықтан, бұл мәселенің физикалық мағынысымен тікелей байланыстығы бар деген қорытынды шығады. Бұл әдіс молекулалқ қозғалыстың динамикасымен қатар олардың соқтығысу статистикасын да қарастырады. Сондықтан да тек молекулалардың орасан зор жиынтығының қозғалысын сипаттайтын орташа шамалары ғана паидалынады, демек ықтималдық жорамалдары қолданады. Бірақ, статистикалық механиканың әдістерінің ықтималдық жорамалдау дәрежесі өте жоғары, себебі барлық практикалық нәтижелердің олар дұрыстығымен теңеседі.Сонымен статистикалық әдісте ықтималдық нәтижелер деген, эксперементтік және теориялық термодинамикадағы нағыз дәл нәтижелер деп есептеледі. Бұл тұрғыдан алғанда, статистикалық орташаланған шамалар арқылы сипаталады.
Осыдан орташа шамаларды есептеудің статистикалық әдістегі маңызының зор екенін көреміз, себебі ол теорияның эксперементтік дәлелдеуінің негізін құрайды.
Уақыт бойынша жүйенің эволютциясын зерттеудің ұқсас жүйелер жиынтығын зерттеумен ауыстыру – статистикалық әдістің негізін құрайды. Мұндай тәсіл ғылымда көптен бір қолданады. Мысалы,астрономияда жұлдыздар жүйесін эвоютциясын зерттеиді. Бірақ жұлдыздар орны ғылымда өте баяу өзгереді, олардың өзгеруін уақыт аралығында адамзат байқай алмайды. Сондықтан, астрономдар жеке жұлдыздың эволютциясын уақт бойынша бақылаудың орнына ұқсас көптеген жұлдыздар жиынтығының күйін әр түрлі даму кезеңінде бақылайды. Сонымен жеке бір жұлдызды, ұқсас жұлдыздарға тән барлық даму кезеңдеріне өтетін деп, тап осы зерттеп отырған жұлдыздың уақыты бойынша эволютциясын бейнелеуге болады деп болжайды. Онда жеке жүйені зеттегенше, оған өзара ұқсас жүйелердің жиынрығын қарастыруға болады. Мұндай жүйелердің жиынтығын ансамбель дейтінін айтып кеттік. Мысалы ретінде ыдыстардағы газды алуға болады. Ондағы жүиелердің күйлері ұқсас, көлемі бірдей ыдыстарда орналасқан және молекулалар саны, типтері де,бірдей болуы есте сақтау керек.
Бірақ жүйелердің айырмашылығы бар, ол әр түрлі алғашқы жағдайларына қатысты жүйенің әр түрлі динамикалық күйде болуында.
Ансамбль және үлестіру функциясы деген ұғымдары келесі тарауда қарастырамыз.
Айта кету керек, статистикалық әдіс жеке жүйенің орнына жүйелер ансамбелін қарастырады және осы ансамбль бойынша анықталған орташаларды соның ішінде жүйені сипаттау үшін қолданылады.
Өзін-өзі бақылау сұрақтары:
1. Молекулалық қозғалыстың кинематикалық сипаттамалары.
2. Эйнштейн заңы.
Қолданылған әдебиеттер:
1. Савельев И.В. Жалпы физика курсы, І том. Механика, тербелістер мен толқындар, молекулалық физика. Савельев И.В. «Наука» баспасы, физика-математика әдебиетінің бас редакциясы, М., 1970 ж. 403 б.
2. С.Э. Фриш және А.Б. Тиморева. Жалпы физика курсы, І том. «Мектеп» баспасы, А., 1971 ж. 269 б.
3. Абдулаев Ж. Жалпы физика курсы: Оқу құралы / Ж. Абдулаев.- Алматы: Ана тiлi, 1991.- 410-420 б
