ЗАДАЧИ ПО СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Задача. С какой скоростью движется тело, если его продольные размеры уменьшились на 30%? Ответ: 0,71 c.
Решение.
Согласно условию длина тела 
для движущегося наблюдателя составляет 0,70 от собственной длины тела 
:
Сопоставив с формулой
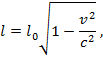
получим
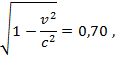
откуда и найдем скорость тела.
Возведем обе части в квадрат
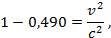
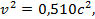
Задача. С какой скоростью должна двигаться частица, чтобы наблюдатель мог ее «видеть» в течение времени в тысячу раз большем ее собственного времени жизни? Ответ: 0,9999995 c.
Решение.
Согласно условию время жизни частицы для движущегося относительно нее наблюдателя 
в тысячу раз больше ее собственного времени жизни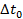 
:
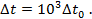
Из формулы
получим
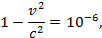
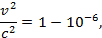
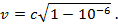
Для извлечения корня воспользуемся формулой приближенного вычисления
Предлагаю проверить верность этой формулы путем возведения обеих частей равенства в квадрат.
Поскольку 
, получим
Предлагаю проверить верность результат на калькуляторе.
Задача. Во сколько раз замедлится время жизни частицы, если она движется относительно наблюдателя со скоростью, составляющей 99 % от скорости света? Ответ: в 7,1 раз.
Решение.
Задача. Найдите релятивистский импульс и релятивистскую энергию частицы массы 
, движущейся со скоростью, составляющей 50% от скорости света.
Решение.
Согласно условию
Релятивистский импульс найдем по формуле
Релятивистскуюэнергию найдем по формуле
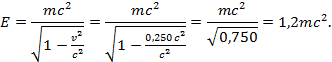
Ответ: 
, 
.
Задача. Найдите скорость частицы, если ее релятивистский импульс в 5 раз больше классического.
Решение.
Согласно условию
Скорость частицы при заданном значении релятивистского импульса можно найти по формуле
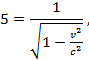
Возведем обе части в квадрат
Ответ: 
Задача. Найдите скорость частицы, если ее релятивистская энергия в 4 раза больше энергии покоя.
Решение.
Согласно условию
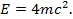
Скорость частицы при заданном значении релятивистской энергии можно найти по формуле
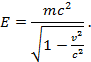
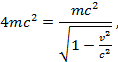
Возведем обе части в квадрат
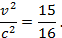
Ответ: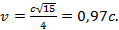 
Задача. Найдите скорость частицы, если ее полная энергия в 4 раза больше кинетической. Ответ: 0,66 c (c 
/ 4).
Решение.
Согласно условию и определению релятивистской кинетической энергии имеем
откуда
Сопоставив с формулой полной релятивистской энергии
получим
Далее
Задача. Полная энергия частицы с массой m в 5 раз больше ее кинетической энергии. Найдите импульс частицы.
Решение.
Согласно условию 
. Так как кинетическая энергия больше не понадобится, выразим ее через полную энергию: 
. Далее по определению кинетической энергии
откуда
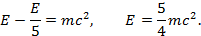
Далее используем формулу связи релятивистской энергии с релятивистским импульсом
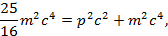
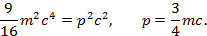
ПРИМЕРЫ ТОЛКОВАНИЯ ФОРМУЛ
Все формулы подразделяются на следующие виды:
1. Формулы определения какой-то физической величины.
2. Формулы некоторого физического закона.
3. Формулы расчета какой-то физической величины.
4. Формулы связи между физическими величинами.
Приведем примеры.
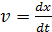.– формула определения проекции скорости на ось 
.
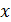– формула определения углового ускорения.
– формула определения вектора напряженности электрического поля.
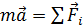– формула второго закона Ньютона.
– формула закона сохранения момента импульса.
– формула расчета потенциала электрического поля, созданного точечным зарядом.
– формула связи между вектором напряженности электрического поля и потенциалом в интегральной форме.
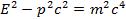– формула связи между релятивистской энергией, релятивистским импульсом и массой тела.
Можно дать толкование формулы, просто расшифровав словами данное равенство. Например:
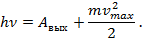
Произведение постоянной Планка 
на частоту света 
равно сумме работы выхода электронов из металла 
и максимальной кинетической энергии этих электронов, где – масса электронов, а 
– их максимальная скорость.
