При расчете размерных цепей (РЦ) по методу максимума-минимума точность замыкающего звена достигается у 100% экземпляров изделий; таким образом, выполняется условие полной взаимозаменяемости.
Вместе с очевидным достоинством данного метода, в результате его применения допуски составляющих звеньев получаются более жесткими (т.е. поля допусков – более узкими), чем это необходимо для попадания значения замыкающего размера в заданные эксплуатационные границы. Неоправданное ужесточение допусков связано с тем, что при расчете по максимуму-минимуму не исключаются любые, даже самые маловероятные сочетания размеров.
Все размеры в основной формуле расчета РЦ
(6.12)
являются величинами случайными, т. к. при изготовлении деталей рассеивание размеров их элементов вызывается случайными вариациями множества действующих факторов.
Следовательно, к расчету РЦ можно применить положения теории вероятностей в отношении суммирования случайных величин, а именно теоремы о сложении математических ожиданий и дисперсий. Согласно первой из них математическое ожидание суммы нескольких случайных величин равно сумме их математических ожиданий:
. (6.13)
Согласно другой теореме дисперсия суммы случайных величин (то есть результирующей случайной величины) определяется как сумма дисперсий составляющих случайных величин: 
+ 
, (6.14)
где - Kij корреляционный момент величин Xi Xj; знак i < j означает, что суммирование распространяется на все возможные сочетания слагаемых.
Для слабо коррелированных случайных величин, каковыми являются отклонения размеров составляющих звеньев, все корреляционные моменты можно принять равными нулю (Kij=0).
Дисперсия, будучи мерой рассеивания случайной величины, связана с шириной T поля допуска следующей формулой:
, (6.15)
где σ – среднее квадратичное отклонение.
Последняя запись (6.15) выражает по сути известное «правило трех сигма» для нормального закона распределения случайной величины. Именно этот закон обычно имеет место для действительных размеров звеньев, т. к. их отклонения вызваны множеством не зависящих друг от друга причин, влияние ни одной из которых не доминирует.
На приведенном далее рисунке показано поле допуска размера вместе с графиком функции плотность вероятности.
Рис. 6.5. К определению среднего квадратического отклонения по ширине поля допуска
Площадь, ограниченная данной кривой f(x), выражает вероятность попадания действительного отклонения размера в рассматриваемый интервал (Ei, Ej).
При максимальном отклонении от центра рассеивания на величину такая вероятность равна 0,9973. Вероятность непопадания 0,0027 в данный интервал шириной 6σ обычно принимается за нулевую.
На основании трактовки размера как нормально распределенной случайной величины [2, 3] можно записать для коллинеарной РЦ:
. (6.16)
В результате вероятностного подхода к расчету РЦ можно существенно увеличить допуски размеров составляющих звеньев. Расширение же полей допусков размеров составляющих звеньев РЦ хотя бы в 1,5 раза дает удешевление изготовления деталей и всего узла в несколько раз. В то же время допуски, полученные в результате вероятностного расчета, не обеспечивают полной взаимозаменяемости, то есть «плата» за указанный выигрыш в стоимости – некоторый, пусть пренебрежимо малый, риск нарушения взаимозаменяемости при сборке.
Ранее изложенная методика решения задачи проектного расчета РЦ при вероятностном подходе видоизменяется следующим образом.
Среднее число единиц допуска находится по формуле:
. (6.17)
Полученные значения nср округляются до стандартных из ряда предпочтительных чисел, после чего выбираются №№ приемлемых квалитетов и проверяются условия:
; 
. (6.18)
Выбор стандартных допусков – промежуточный результат при решении задачи проектного расчета РЦ; конечная же цель - определение границ полей допусков, то есть предельных отклонений.
Предельные отклонения находятся из приводимых ниже формул, каждая из которых связывает верхнее Es, нижнее Ei и среднее Em отклонения соответствующего размера:
Es(AΔ) = Em(AΔ) + TΔ/2; (6.19)
Ei(AΔ) = Em(AΔ) - TΔ/2; (6.20)
Es(Aj) = Em(Aj) + ITj/2; (6.21)
Es(Aj) = Em(Aj) - ITj/2. (6.22)
Формулы (6.19), (6.20) записаны в отношении поля допуска замыкающего звена (размера), а формулы (6.21), (6.22) – для полей допусков составляющих размеров.
Рис.6.5 иллюстрирует приведенные выше формулы для случая нормальной функции плотность вероятности f(x); здесь x – случайная величина отклонения размера.
При имеющей место симметричности функции f(x)
. (6.23)
Из основного соотношения, связывающего номинальные размеры звеньев цепи, следует:
. (6.24)
Как и при расчете методом максимума- минимума (полная взаимозаменяемость – см. выше) поля допусков размеров составляющих звеньев назначаются: как для основного вала (ряд основного отклонения h), если размер относится к охватываемому элементу; в этом случае Em(Aj) = - ITj/2; как для основного отверстия (ряд основного отклонения H), если размер относится к охватывающему элементу; тогда Em(Aj) = + ITj/2; симметричными относительно линии номинального размера в остальных случаях, что соответствует Em(Aj)=0.
И одно звено необходимо оставить в качестве увязочного (резервного). В качестве резервного звена рекомендуется выбирать достаточно большое по номинальному размеру звено; оно может быть как увеличивающим 
", так и уменьшающим 
; желательно, чтобы закон распределения отклонения размера этого звена был нормальный.
Для нормальной коллинеарной цепи при симметричности функции f(x) среднее отклонение резервного звена определяется:
; (6.25)
. (6.26)
Изложенная методика иллюстрируется примером расчета РЦ (рис. 6.6), которая была ранее рассчитана методом полной взаимозаменяемости.
Рис. 6.6. Схема размерной цепи
Задача проектного расчета РЦ вероятностным методом решается далее при тех же, что и ранее исходных данных:
А1 = А3 = 10 мм; А2 = 80 мм; А4 = 60 мм.
40 ≤ А ≤ 150 мкм.
Искомые величины – предельные отклонения составляющих размеров,ES (Aj), Ei (Aj), j = 1,..,4.
Значения единиц допуска звеньев: i1,3 = 0,9 мкм; i2, 4 = 1,9 мкм.
Среднее число единиц допуска, согласно формуле (6.17) равно:
.
Полученное число позволяет назначать допуски размеров цепи по квалитетам 8 и 9.
Т1 = Т3 = IT9 = 36 мкм; Т2 = IT9 =74 мкм; Т4 = IT8 = 46 мкм.
Эти допуски позволяют достаточно рационально удовлетворить условию задачи: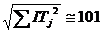 
мкм.
Далее необходимо обратиться к уравнению средних отклонений размеров и, назначив резервным звеном А2, принимая ES1,3 = - Ei1,3 = 18 мкм; ES4 = 0; Ei4 = - 46 мкм, вычислить середину его поля допуска:
Em2 = EmΔ + Em1 + Em3 + Em4 = 95 + 0 - 23 = 72 мкм.
Остается только найти предельные отклонения резервного звена: с учетом величины допуска Т2 = 74 мкм получаем
ES2 = 109 мкм; Ei2 = 35 мкм.
В общем случае (ведь закон распределения не обязательно является нормальным) вводят безразмерный коэффициент αj относительной асимметрии функции f(x).
