Этот закон занимает особое место среди всех распределений.
Погрешность реализации размера (элемента детали) может быть представлена суммой элементарных погрешностей, каждая из которых вызвана действием отдельной причины, не зависящей от остальных (изменения температуры, не идеальность оборудования, износ инструмента, субъективные факторы и др.). Если ни один из влияющих факторов не превалирует, то суммарная погрешность ΔΣ оказывается подчиненной предельному закону - закону Гаусса, каким бы законам распределения ни были бы подчинены отдельные погрешности Δi, составляющие сумму ΣΔi = ΔΣ [ 1 ].
Вот почему уже давно для оценки случайных погрешностей принят закон Гаусса – нормальный закон распределения. Плотность этого распределения - дифференциальная функция f(x) - представляется трансцендентной кривой, известной под названием «колокол»:
 . (6.5)
. (6.5)

Рис. 6.3. Плотность вероятностей нормального закона распределения (закона Гаусса)
Здесь m – математическое ожидание; σ – среднее квадратическое отклонение.
Если дифференциальная функция распределения f(x) известна, то вероятность попадания СВ в доверительные границы (x1, x2) вычисляют как
 , (6.6)
, (6.6)
где в рассматриваемом случае нормального закона распределения трансцендентная функция f(x) затрудняет вычисление искомой вероятности.
Для облегчения вычислений придумали нормированную функцию f(z),
где z = (x - m) / σ. (6.7)
Переход к этой функции можно представить поэтапно. Сначала осуществляется переход к центрированной СВ и, соответственно, к функции f(x-m), симметричной относительно начала координат; в зависимости от величины σ полученная на этом этапе функция будет больше или меньше растянута (сжата) вдоль оси x. Далее - с целью перехода к единой (нормированной) функции - осуществляют замену переменной (6.7).
Таким образом, нахождение вероятности попадания СВ в заданный интервал уже не связано с вычислением интеграла
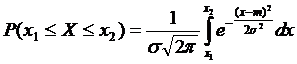 , (6.8)
, (6.8)
«индивидуального» в каждой конкретной задаче со своими параметрами m и σ, а сводится к нахождению инвариантного к величинам m и σ интеграла
 . (6.9)
. (6.9)
Теперь для нахождения значений этого интеграла по таблицам остается сделать последний шаг: оставить только один меняющийся в зависимости от условий задачи предел интегрирования. Таким шагом является введение следующей функции:
 , (6.10)
, (6.10)
которая известна, как функция Лапласа. Вид данной функции и ее соответствие плотности распределения f(z) показан на рис. 6.4.
Значение функции Лапласа (нечетной функции) какого-либо аргумента Ф(z*) есть ни что иное как вероятность попадания СВ z в интервал (0, z*). Очевидно, что вероятность попадания СВ в интервал (0, ∞) равна 0,5. Такова же вероятность попадания СВ и в интервал (- ∞, 0).

Рис. 6.4. Функция Лапласа Ф(z) и плотность распределения f(z)
В общем случае вероятность попадания СВ z в интервал (z1, z2), а, следовательно, величины x в интервал (x 1, x 2), рассчитывается по формуле
 =
= 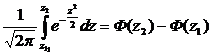 (6.11)
(6.11)
Таблица значений функции Лапласа представлена ниже.
 Таблица 6.2. Значения функции Лапласа
Таблица 6.2. Значения функции Лапласа
| z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0,0 | 0,0000 | 0,0040 | 0,0080 | 0,0120 | 0,0160 | 0,0199 | 0,0239 | 0,0279 | 0,0319 | 0,0359 |
| 0,1 | 0398 | 0438 | 0478 | 0517 | 0557 | 0596 | 0636 | 0675 | 0714 | 0753 |
| 0,2 | 0793 | 0832 | 0871 | 0910 | 0948 | 0987 | 1026 | 1064 | 1103 | 1141 |
| 0,3 | 1179 | 1217 | 1255 | 1293 | 1331 | 1368 | 1406 | 1443 | 1480 | 1517 |
| 0,4 | 1554 | 1591 | 1628 | 1664 | 1700 | 1736 | 1772 | 1808 | 1844 | 1879 |
| 0,5 | 1915 | 1950 | `985 | 2019 | 2054 | 2088 | 2123 | 2157 | 2190 | 2224 |
| 0,6 | 2257 | 2291 | 2324 | 2357 | 2389 | 2422 | 2454 | 2486 | 2517 | 2549 |
| 0,7 | 2580 | 2611 | 2642 | 2673 | 2703 | 2734 | 2764 | 2794 | 2823 | 2852 |
| 0,8 | 2881 | 2910 | 2939 | 2967 | 2995 | 3023 | 3051 | 3078 | 3106 | 3133 |
| 0,9 | 3159 | 3186 | 3212 | 3238 | 3264 | 3289 | 3315 | 3340 | 3365 | 3389 |
| 1,0 | 3413 | 3438 | 3461 | 3485 | 3508 | 3531 | 3554 | 3577 | 3599 | 3621 |
| 1,1 | 3643 | 3665 | 3686 | 3708 | 3729 | 3749 | 3770 | 3790 | 3810 | 3830 |
| 1,2 | 3849 | 3869 | 3888 | 3907 | 3925 | 3944 | 3962 | 3980 | 3997 | 4015 |
| 1,3 | 4032 | 4049 | 4066 | 4082 | 4099 | 4115 | 4131 | 4147 | 4162 | 4177 |
| 1,4 | 4192 | 4207 | 4222 | 4236 | 4251 | 4265 | 4279 | 4292 | 4306 | 4319 |
| 1,5 | 4332 | 4345 | 4357 | 4370 | 4382 | 4394 | 4406 | 4418 | 4429 | 4441 |
| 1,6 | 4452 | 4463 | 4474 | 4484 | 4495 | 4505 | 4515 | 4525 | 4535 | 4545 |
| 1,7 | 4554 | 4564 | 4573 | 4582 | 4591 | 4599 | 4608 | 4616 | 4625 | 4633 |
| 1,8 | 4641 | 4649 | 4656 | 4664 | 4671 | 4678 | 4686 | 4693 | 4699 | 4706 |
| 1,9 | 4713 | 4719 | 4726 | 4732 | 4738 | 4744 | 4750 | 4756 | 4761 | 4767 |
| 2,0 | 4772 | 4778 | 4783 | 4788 | 4793 | 4798 | 4803 | 4808 | 4813 | 4817 |
| 2,1 | 4821 | 4826 | 4830 | 4834 | 4838 | 4812 | 4846 | 4850 | 4854 | 4857 |
| 2,2 | 4861 | 4864 | 4868 | 4871 | 4874 | 4878 | 4881 | 4884 | 4887 | 4890 |
| 2,3 | 4893 | 4896 | 4898 | 4901 | 4904 | 4906 | 4909 | 4911 | 4913 | 4916 |
| 2,4 | 4918 | 4920 | 4922 | 4925 | 4927 | 4929 | 4931 | 4932 | 4934 | 4936 |
| 2,5 | 4938 | 4940 | 4941 | 4943 | 4945 | 4946 | 4948 | 4949 | 4951 | 4952 |
| 2,6 | 4953 | 4955 | 4956 | 4957 | 4959 | 4960 | 4961 | 4962 | 4963 | 4964 |
| 2,7 | 4965 | 4966 | 4967 | 4968 | 4969 | 4970 | 4971 | 4972 | 4973 | 4974 |
| 2,8 | 4974 | 4975 | 4976 | 4977 | 4977 | 4978 | 4979 | 4979 | 4980 | 4981 |
| 2,9 | 4981 | 4982 | 4982 | 4983 | 4984 | 4984 | 4985 | 4985 | 4986 | 4986 |
| 3,0 | 4986 | |||||||||
| 3,5 | 4998 | |||||||||
| 4,0 | 4999 |
Вот как определяется с помощью данной таблицы вероятность попадания СВ z в интервал (-3, +3).
Ф(3) = 0, 4986, следовательно P(-3 ≤ z ≤ 3) = 2 Ф(3) = 0,9972. Известно, что для нормально распределенной СВ x интервал (m - 3σ, m + 3σ) считается интервалом практической достоверности. Такой способ оценки диапазона возможных значений СВ называют «правилом трех сигма».






