Методы отделения корней НЛУ

Существует 3 основных метода отделения корней:

 

1) графический;

2) аналитический;

3) численный.

 

Ни один из них не является универсальным, и на практике эти методы применяются в совокупности. В простейших случаях можно ограничиться каким–то одним из них.

Графическое отделение корней основано на отыскании точек, в которых функция f(x) пересекает ось абсцисс. На слайде 5 изображен график функции f (x) = ln (x – 1)² – 0.5, из которого следует, что уравнение

 

ln (x – 1)²–0.5=0

имеет два действительных корня: .

В некоторых случаях бывает удобнее вначале преобразовать функцию f (x) к виду f (x) = g ₁ (x) - g ₂ (x), а уравнение – к виду g ₁ (x) = g ₂ (x). Тогда отрезки отделения корней должны содержать абсциссы точек пересечения графиков g ₁ (x) и g ₂ (x). На слайде 6 иллюстрируется такой способ графического отделения корней для уравнения с os (x) – x + 1 = 0. Из графиков видно, что корень уравнения .

Аналитическое отделение корней основано на следующих известных свойствах непрерывных функций:

1. Если функция f(x) непрерывна на отрезке [a;b] и на концах отрезка имеет противоположные знаки (f (a) ∙ f (b) < 0), то отрезок [a;b] содержит хотя бы один корень уравнения f (x) = 0 (слайд 7).

2. Если при этом f(x) имеет на отрезке [a;b] знакопостоянную первую производную f'(x), то есть если f(x) монотонна, то корень единственный (слайд 8).

Проверим, например, условие существования и единственности корня уравнения cos (x) – x + 1 = 0 на отрезке [1;2] (слайд 9). На концах отрезка функция f(x) имеет противоположные знаки:

f(1) = cos (1) – 1 + 1 = 0.54, f (2) = cos (2) – 2 + 1 = -1.42,

следовательно на отрезке [1;2] имеется хотя бы один корень.

Производная f'(x) = – sin (x) на отрезке [1;2] отрицательна, следовательно, этот корень единственный.

При отделении корней алгебраических уравнений можно также дополнительно пользоваться следующими свойствами полиномов (слайд 10):

1. Полином степени n имеет в точности n действительных или комплексных корней.

2. Число действительных корней полинома равно или на четное число меньше его степени n.

3. Число положительных корней равно или на четное число меньше числа перемен знаков в последовательности коэффициентов a_i.

4. Число отрицательных корней равно или на четное число меньше числа перемен знаков в последовательности коэффициентов a_i, полученной при замене x на – x.

Например (слайд 11), уравнение x³ – x + 1 = 0 имеет 3 действительных или комплексных корня. Число действительных корней равно 3 или 1.

Последовательность коэффициентов имеет 2 перемены знака, следовательно, число положительных корней равно 2 или 0.

Последовательность коэффициентов после замены x на – x имеет 1 перемену знака, следовательно, число отрицательных корней равно 1.

При x >= 0 функция f (x) = x³ – x + 1 > 0, следовательно, положительных корней нет.

f (0) = 1 > 0, а f (-2) = -5 < 0, следовательно единственный  отрицательный корень уравнения принадлежит отрезку [–2;0].

При численном отделении корней (слайд 12) с помощью программы или математического пакета вычисляется таблица значений функции f(x) в некоторой области значений x с достаточно малым шагом. По полученной таблице определяются отрезки, на концах которых функция меняет знак, и, следовательно, внутри отрезков находятся корни уравнения.

После того, как корни уравнения отделены, можно приступать к уточнению всех или некоторых корней. Рассмотрим методы уточнения корня НЛУ.

 

Метод половинного деления

Пусть корень уравнения f (x) = 0 отделен на отрезке [ a; b ], то есть f (a)∙ f (b) < 0. Найдем середину отрезка c = (a + b)/2. Если f(c)∙ f (b) < 0 (слайд 13а), то корень находится на отрезке [c;b], и этот отрезок становится новым отрезком отделения корня. При этом левая граница отрезка a переносится в точку c.

Затем новый отрезок [a;b] опять делится пополам точкой c (слайд 13б). Теперь оказывается f(c)∙ f (а) < 0, то есть корень принадлежит отрезку [a;c]. Точка b переносится в точку c, и получается следующий отрезок отделения корня [a;b].

Продолжая этот процесс, получим последовательность вложенных отрезков [a;b], таких что f (a)∙ f (b) < 0 и длина каждого последующего отрезка вдвое меньше длины предыдущего.

Последовательное сужение отрезка вокруг неизвестного значения корня x ^* приведет к тому, что на некотором шаге n длина отрезка станет меньше наперед заданной погрешности ε (b_n - a_n < e). Поскольку при этом для любого х Î [ a_n; b_n ] будет выполняться неравенство | х - x ^* | < , то с погрешностью ε  любое х Î [ a_n; b_n ] может быть принято за приближенное значение корня (слайд 14). Обычно в качестве приближенного значения корня берется середина отрезка .

Так как , то для достижения заданной точности необходимо, чтобы  

Если функция f(x) непрерывна на отрезке [a;b], то метод половинного деления всегда сходится. Однако скорость сходимости у этого метода невысокая. Так при начальной длине отрезка b₀ – a₀ = 1 и допустимой погрешности ε = 10^-6 требуемое количество итераций n составит более 20.

На слайде 15 изображена схема алгоритма процедуры уточнения корня НЛУ методом половинного деления. Входными параметрами процедуры являются границы отрезка отделения корня a и b, а также допустимая погрешность приближенного вычисления корня E. Результат выполнения процедуры формируется в переменной c. Предполагается, что для вычисления функции в левой части уравнения имеется процедура f(x). Использование вспомогательных переменных fa и fc позволяет при каждом повторении цикла вычислять новое значение функции только один раз.

Метод простой итерации

 

Преобразуем уравнение f (x) = 0 в равносильное уравнение x = φ(x). Такое преобразование можно выполнить множеством различных способов (слайд 16). Пусть дано уравнение x² – sin x = 0. Тогда возможны, например, следующие способы преобразования:

 

x = x + x ² – sin x

x = √sin x

x = arc sin x²

На выборе способа преобразования остановимся позже.

В методе простой итерации последовательность приближений к корню строится по правилу:

x_n = φ(x_{n -1}),

 

а функция φ(x) называется итерирующей функцией. Таким образом, задавшись начальным приближением x ₀ Î [ a; b ], можно получить последовательность приближение к корню:

 

x ₁ = j (x ₀), x ₂ = j (x ₁), …, x_n = j (x_{n -1}), …

которая при выполнении некоторых условий сходится к точному значению корня x^*, то есть

 

Прежде чем будут сформулированы условия сходимости метода, рассмотрим его геометрическую иллюстрацию.

Построим графики функций y = x и y = j (x) (слайд 17, левый рисунок). Корень уравнения х= j (x) является абсциссой точки пересечения этих графиков. Возьмем некоторое начальное приближение x ₀ Î [ a; b ]. На кривой y = j (x) ему соответствует точка А₀ = j (x ₀). Чтобы найти очередное приближение, проведем через точку А₀ прямую горизонтальную линию до пересечения с прямой y = x (точка В₁) и опустим перпендикуляр до пересечения с осью x. Так как на прямой y=x абсцисса любой точки равна ее ординате, то х₁= j (x ₀). Продолжив построения аналогичным образом, получим ломаную линию (“лестницу”) А₀, В₁, А₁, В₂, А₂…, для которой общие абсциссы точек представляют собой последовательные приближения х₁, х₂, …, х _n к корню х*.

Из рисунка видно, что процесс приближений сходится к корню уравнения, причем последовательность приближений моготонна. Заметим, что в этом случае производная функции φ(x) в области существования корня положительна и не превышает 1 (крутизна кривой φ(x) меньше крутизны прямой y =x).

Проведем аналогичные построения для другого вида кривой y = j (x) (слайд 17, правый рисунок). В этом случае ломаная линия А₀, В₁, А₁, В₂, А₂ … имеет вид “спирали”. Однако и здесь наблюдается сходимость последовательности приближений к корню, но только эта последовательность не монотонна, а колеблется вокруг точного значения корня. Заметим, что в этом случае производная функции φ(x) в области существования корня отрицательна и по абсолютной величине не превышает 1 (крутизна кривой φ(x) меньше крутизны прямой y = –x).

На рисунках слайда 18 такие же построения проведены для случаев, когда производная функции j (x) по абсолютной величине больше 1, и в этих случаях, как видно из рисунков, последовательность приближений расходится.

Таким образом, сходимость метода простой итерации зависит от свойств первой производной итерирующей функции j (x), а условия сходимости определяются следующей теоремой (слайд 19):

Пусть корень х* уравнения x = j (x) отделен на отрезке [ a; b ] и построена последовательность приближений по правилу x_n = j (x_{n -1}). Тогда, если все члены последовательности x_n = j (x_{n -1}) Î [ a; b ] и существует такое q (0< q <1), что для всех х Î [ a; b ] выполняется  | j ’(x)| ≤ q < 1, то эта последовательность является сходящейся, и пределом последовательности является значение корня x *, т.е. процесс итерации сходится к корню уравнения независимо от начального приближения.

Обычно, если условия сходимости выполняются, то в качестве начального приближения берут середину отрезка [ a; b ] (слайд 20):

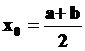
Таким образом, для проверки условия сходимости метода надо найти 

и убедиться, что q < 1. Проверим условия сходимости метода простой итерации для уравнения cos (x) – 3 x + 1 = 0, корень которого отделен на отрезке [0;1] (слайд 21).

Преобразуем уравнение к виду, необходимому для использования метода простой итерации:

x = (cos(x) + 1)/3

Тогда j (x) = (cos(x) + 1)/3, а | j ’(x)| = sin(x)/3. На отрезке [0;1] функция sin(x) монотонно возрастает, достигая максимального значения на правой границе отрезка в точке x = 1. Следовательно,

и метод сходится при любом начальном приближении х₀ Î [0;1].

Получим несколько последовательных приближений по итерационной формуле x _n = (cos(x _{n -1}) + 1)/3 из начального приближения x ₀ = 0 (слайд 22):

 

x₁ = (cos(x₀) + 1)/3 = (cos(0) + 1)/3 = 0.667

x₂ = (cos(x₁) + 1)/3 = (cos(0.667) + 1)/3 = 0.595

x₃ = (cos(x₂) + 1)/3 = (cos(0.595) + 1)/3 = 0.609

x₄ = (cos(x₃) + 1)/3 = (cos(0.609) + 1)/3 = 0.607

Как видно, процесс последовательных приближений сходится.

Можно показать (слайд 23), что погрешность n–го приближения

Как видно из этой формулы, при q>0.5 совпадение с точностью ε двух последовательных приближений x_n и x_n–1 не гарантирует совпадения с той же точностью x_n и x ^*. Так, например, при q=0.9 погрешность | x_n – x ^* | почти на порядок может превышать величину | x_n – x_{n -1} |.

Таким образом, чтобы обеспечить заданную погрешность приближения | x_n – x ^* | <= ε, необходимо выполнение неравенства

откуда получаем правило останова: