Пусть корень уравнения f (x)=0 отделен на отрезке [ a; b ], причем первая и вторая производные f ’(x) и f ''(x) непрерывны и знакопостоянны при х Î [ a; b ].
В этом случае для построения последовательности приближений к корню может быть использован метод Ньютона: каждое следующее приближение xn вычисляется через предыдущее приближение xn–1 по формуле:
Таким образом, задавшись начальным приближением x0 можно получить первое приближение
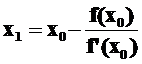
затем второе
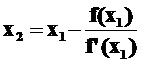
и так далее до получения приближения, погрешность которого не превышает заданную.
Как и в случае метода простой итерации возникают вопросы:
1) при каких условиях получаемая методом Ньютона последовательность приближения сходится к точному значению корня x*;
2) как выбрать начальное приближение x0;
3) как, не зная точного значения корня x* определить, что заданная точность достигнута.
Для ответов на эти вопросы рассмотрим геометрическую иллюстрацию метода Ньютона (слайд 3). В точке начального приближения x0 восставим перпендикуляр к оси X до пересечения с кривой y = f(x). В полученной точке пересечения проведем касательную к кривой y = f(x) до пересечения с осью X: получим первое приближение x1. В точке x1 снова восставим перпендикуляр к оси X до пересечения с кривой y = f(x), а в полученной точке пересечения вновь проведем касательную к кривой и получим второе приближение x2.
Продолжая процесс таких построений, мы, как видно из рисунка, получаем последовательность приближений, стремящуюся к точному значению корня x*. На слайде 4 показано, что последовательность проделанных построений соответствует формуле метода Ньютона, и, наоборот, формула метода Ньютона может быть выведена из геометрических построений. Исходя из геометрического смысла метода Ньютона, его называют также методом касательных.
На слайде 3 кривая y=f(x) проведена так, что производные f'(x) и f''(x) имеют постоянный знак (обе положительны). Является ли это обязательным условием для сходимости метода Ньютона? На слайде 5 показано, что может произойти при нарушении знакопостоянства производных. Здесь кривая y= f(x) имеет экстремумы (изменение знака первой производной) и точки перегиба (изменение знака второй производной). Начав приближения из точки x1, мы попадаем сначала в точку x2, удаляясь от корня r, а затем в точку x3, лежащую вообще вне области определения функции f(x).
На слайде 6 показано, что даже при знакопостоянстве производных f(x) метод Ньютона чувствителен к выбору начального приближения. Пусть, как это показано на рисунке, на отрезке [a; b ] первая и вторая производные сохраняют свои знаки (обе положительны). Если выбрать начальное приближение x0 на правом конце отрезка, в точке b, то последовательность приближений, как и на слайде 3, ведет к точному значению корня. Если же выбрать начальное приближение на левом конце отрезка, в точке a, то касательная к кривой в точке a выводит нас за пределы отрезка (правее точки b), где о поведении функции и ее производных нам ничего не известно. При благоприятных условиях мы вернемся в пределы отрезка [a; b ], и нормальный ход процесса восстановится, но рассчитывать на это не стоит.
Заметим, что “хороший” выбор начального приближения x0=b соответствует совпадению в точке x0 знаков функции и второй производной, а “плохой” – несовпадению.
Теперь мы можем, наконец, сформулировать теорему о сходимости метода Ньютона (слайд 7):
Пусть корень уравнения f(x) = 0 отделен на отрезке [a;b] (функция f(x) непрерывна на [a;b] и на концах его принимает разные знаки), а производные f'(x) и f''(x) отличны от нуля и сохраняют постоянные знаки на [a;b]. Тогда, если выбрать начальное приближение х0 Î [ a; b ] так, чтобы f'(x0) ∙ f''(x0) > 0, то последовательность приближений, определяемая формулой
сходится.
Проверим условия сходимости метода Ньютона и выберем начальное приближение для уравнения cos (x) – 3 x + 1 = 0, корень которого отделен на отрезке [0;1] на прошлой лекции (слайд 8).
Первая производная f'(x) = – sin (x) – 3 < 0 при любых значениях x. Вторая производная f''(x) = – cos (x) < 0 на отрезке [0;1]. Следовательно, последовательность приближений по методу Ньютона будет сходящейся при выборе начального приближения так, чтобы f(x0) < 0. Это условие выполняется на правом конце отрезка: x0 = 1.
Получим несколько последовательных приближений по итерационной формуле Ньютона
из начального приближения x0 = 1 (слайд 9):
x1 = x0 – (cos(x0) – 3x0 + 1)/(-sin(x0) – 3) = 1 – (0.54 – 3 + 1)/(-0.84 - 3) = 0.62
x2 = x1 – (cos(x1) – 3x1 + 1)/(-sin(x1) – 3) = 0.62 – (0.814 – 1.86 + 1)/(-0.581 - 3) = =0.607
x3 = x2 – (cos(x2) – 3x2 + 1)/(-sin(x2) – 3)=0.607 – (0.821 – 1.821 + 1)/(-0.57 - 3)= =0.607
Как видно, процесс последовательных приближений сходится.
Можно показать (слайд 10), что погрешность n–го приближения
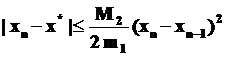
где m 1 – наименьшее значение |f'(x)| при 
M2 – наибольшее значение | f ’’(x)| при 
Таким образом, если задана допустимая погрешность приближения к корню ε, то процесс последовательных приближений можно прекратить при выполнении условия:
Существует и другой, универсальный способ оценки погрешности приближения и соответствующее ему правило останова. Этот способ применим к любому методу уточнения корня, но требует дополнительного вычисления функции в точке очередного приближения:
где m 1 – наименьшее значение |f'(x)| при
С точки зрения программной реализации более удобным является первый способ, основанный на сравнении двух последовательных приближений, и мы будем пользоваться именно им.
На слайде 11 изображена схема алгоритма процедуры уточнения корня НЛУ методом Ньютона. Входными параметрами процедуры являются начальное приближение к корню x, допустимая погрешность приближенного вычисления корня E, минимальноезначение первой производной m 1 и максимальное значение второй производной M2. Результат выполнения процедуры формируется в переменной x. Предполагается, что для вычисления функции f (x) имеется процедура F(x), а для вычисления ее производной f ’(x) – процедура F1(x).
Метод хорд
Пусть корень уравнения f (x)=0 отделен на отрезке [ a; b ], причем первая и вторая производные f ’(x) и f ''(x) непрерывны и знакопостоянны при х Î [ a; b ]. Для построения последовательности приближений по методу хорд рассмотрим сначала геометрическую иллюстрацию этого метода.
На слайде 12 изображен случай, когда обе производные f’(x) и f ’’(x) положительны на отрезке отделения корня. Проведем отрезок прямой через точки A и B и постоим уравнение этой хорды:
 |
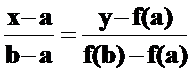Примем за начальное приближение x0 левую границу отрезка x0 = a, а за следующее приближение x 1 – точку пересечения хорды с осью O x, в которой y = 0. Тогда из уравнения хорды получим:
 |
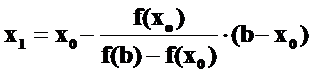В найденной точке x1 получим точку A1 на кривой y =f(x), и проделаем те же построения. Пересечение новой хорды с осью Ox даст следующее приближение x2:
Повторяя эти построения на n–ой итерации получим:
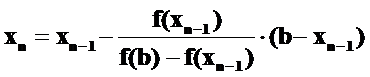
Рассмотрим теперь случай, когда f'(x) > 0, а f''(x) < 0 (слайд 13). Здесь уравнение хорды, проведенной через точки на кривой y=f(x), соответствующие концам отрезка a и b, имеет следующий вид:
Здесь за начальное приближение принимается правая граница отрезка x0 = b, и последовательность приближений получается следующим образом:
 |
 |
………………………………………
 |
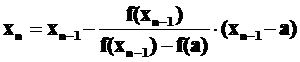Аналогичные построения могут быть проведены и для случаев, когда первая производная f'(x) < 0 на отрезке [a;b].
Из рассмотренных построений видно, что один из концов отрезка отделения корня в процессе итераций остается неподвижным, а противоположный конец вначале принимается за начальное приближение, а затем постепенно смещается в сторону корня, образуя последовательность приближений. Общее правило таково (слайд 14):
за неподвижную точку в методе хорд выбирается тот конец отрезка [a;b], на котором знак функции совпадает со знаком второй производной: f(x)∙ f ’’(x)>0; в качестве начального приближения выбирается противоположный конец отрезка.
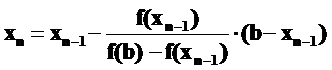Получим несколько последовательных приближений методом хорд для уравнения cos (x) – 3 x + 1 = 0, корень которого отделен на отрезке [0;1]. Условия сходимости метода для этого уравнения совпадают с условиями сходимости метода Ньютона и были нами проверены ранее. Так как вторая производная f''(x)<0, за неподвижную точку принимаем правую границу отрезка b=1, где f(b)=-1.4597<0, за начальное приближение – x0=a=0, и используем итерационную формулу
В результате получаем (слайд 15):
x 1 = x 0 – (cos (x 0) – 3 x 0 + 1)/(-1.4597- cos (x 0) – 3 x 0 + 1)∙(1- x 0) =
= 0 – 2/(-1.4597-2)∙1 = 0.5781
x2 = x1 – (cos (x1) – 3x1 + 1)/(-1.4597- cos (x1) – 3x1 + 1)∙(1- x1) =
= 0.5781 – 0.1028/(-1.4597-0.1028)∙(1-0.5781) = 0.6059
x3 = x2 – (cos (x2) – 3x2 + 1)/(-1.4597- cos (x2) – 3x2 + 1)∙(1- x2) =
= 0.6059 – 0.0043/(-1.4597-0.0043)∙(1-0. 6059) = 0.6070
Как видно, процесс последовательных приближений сходится к тому же корню, что и в методе Ньютона, но с несколько меньшей скоростью.
Можно показать (слайд 16), что погрешность n–го приближения метода хорд
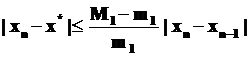
где m 1 – наименьшее значение |f'(x)| при
M1 – наибольшее значение | f ’(x)| при
Таким образом, если задана допустимая погрешность приближения к корню ε, то процесс последовательных приближений можно прекратить при выполнении условия:
На слайде 17 изображена схема алгоритма процедуры уточнения корня НЛУ методом хорд. Входными параметрами процедуры являются начальное приближение к корню x, неподвижная точка c, допустимая погрешность приближенного вычисления корня E, минимальноеи максимальное значения первой производной m 1 и M1. Результат выполнения процедуры формируется в переменной x. Предполагается, что для вычисления функции f (x) имеется процедура F(x).
Неизменяемое значение функции в неподвижной точке F(c) вычисляется один раз перед входом в цикл и запоминается в переменной fc. Значение функции в точке предыдущего приближения F(x), используемое дважды в числителе и знаменателе итерационной формулы, вычисляется на каждой итерации один раз и запоминается в переменной fx.
Заметим, что итерационная формула в схеме алгоритма не зависит от выбора неподвижной точки. При другом выборе неподвижной точки меняются местами уменьшаемое и вычитаемое как в числителе, так и в знаменателе формулы, и таким образом знак частного остается неизменным.
