Имитационное моделирование, как метод проведения системных исследований.

Часть1. Сложные системы и их стохастические модели.

Лекция 1.

Системность - общее свойство материи. Понятие сложной системы. Способы описания систем. Сбор данных о функционировании системы. Построение моделей систем. Отражение свойств системы в математической модели. Анализ и синтез - методы исследования систем. Проверка адекватности моделей, анализ неопределенности и чувствительности.

Имитационное моделирование, как метод проведения системных исследований.

С позиций современных научных представлений системность всегда была методом любой науки. Возможно, что принципы системности применялись не всегда осознанно, но, тем не менее, любой ученый прошлого, который и не помышлял о системном подходе, так или иначе имел дело с системами и моделями объектов или процессов. Ранее всего системные проблемы были осознаны философами. Следует отметить, что обсуждение системных проблем в таких дисциплинах как философия, логика, математика осуществлялось еще древними учеными. Однако в настоящее время представляет особый интерес развитие системных представлений в применении к системным и техническим дисциплинам.

Первым в явной форме вопрос о научном подходе к управлению сложными системами поставил М.-А. Ампер. Он впервые выделил кибернетику как специальную науку об управлении государством, обозначил ее место в ряду других наук и сформулировал ее системные особенности. Идеи системности применительно к управлению государством развивались в работах польского ученого Б. Трентовского. Он отмечал, что действительно эффективное управление должно учитывать все важнейшие внешние и внутренние факторы, влияющие на объект управления. В своих работах Трентовский пишет, что при выработке управляющего воздействия необходимо учитывать национальные особенности населения с учетом временного аспекта, при одной и той же политической идеологии кибернет (в современной терминологии, лицо, принимающее решение) должен управлять различно в Австрии, России или Пруссии, точно так же и в одной и той же стране он должен управлять завтра иначе, чем сегодня. Трентовский рассматривает общество как систему, которая развивается путем разрешения противоречий. И все- таки общество середины 19-го столетия было не готово к восприятию системных представлений. Прошло еще более полувека, прежде чем системная проблематика прочно заняла свое место в научных публикациях. К числу основоположников теории систем можно заслуженно отнести российского ученого, академика Е.С. Федорова. Основные научные результаты были достигнуты им в области минералогии. Он установил, что существует только 230 типов кристаллической решетки, тем не менее, любое вещество при определенных условиях может кристаллизоваться. Таким образом, было показано, что великое многообразие кристаллов и минералов использует для своего строения ограниченное количество типов структур. Далее им были отмечены аналогичные закономерности в области архитектурных и музыкальных 12 конструкций, языковых построений, строения вещества и ряда других систем. Развивая системные представления Федоров установил ряд других закономерностей развития систем, в частности, им было замечено такое свойство систем как самоорганизация, способность к приспособлению, к повышению стройности.

Следующим этапом в развитии системных представлений явились работы А.А. Богданова, который в начале XX в. начал создавать теорию организации (тектологию). Основная идея теории Богданова заключается в том, что все существующие объекты и процессы имеют определенный уровень организованности, который тем выше, чем сильнее свойства целого отличаются от простой суммы свойств комплектующих элементов. Именно анализ свойств целого и его частей был впоследствии заложен в качестве основной характеристики понятия сложной системы. Заслугой Богданова явилось также то, что он изучает не только статическое состояние структур, а занимается исследованием динамического поведения объектов, уделяет внимание вопросам развития организации, подчеркивает значение обратных связей, указывает на необходимость учета собственных целей организации, отмечает роль открытых систем. Он подчеркивает роль моделирования и математических методов как потенциальных методов решения задач теории организации. Позднее идеи теории организации развивались в трудах выдающихся представителей отечественного естествознания И.И. Шмальгаузена, В.Н. Беклемишева и ряда других специалистов, вклад которых во многих отношениях явился решающим в формировании вышеназванной теории. Вклад русских и советских исследователей в развитие теории систем и формирование системных представлений явился определяющим, поскольку большинство развиваемых ныне идей связано с работами Богданова и трудами его последователей.

Однако нельзя не отметить также и зарубежных ученых, работы которых являются основополагающими в области развития теории систем и системного анализа. В первую очередь следует обратить внимание на труды австрийского ученого JI. фон Берталанфи, который в 50-х гг. XX в. организовал в Канаде центр системных исследований. Он опубликовал большое количество работ, в которых исследовал взаимодействие систем с окружающей средой. Подчеркнуто большое значение обмена системы веществом, энергией и энтропией с внешним миром, отмечено, что в системе устанавливается динамическое равновесие, которое может быть направлено в сторону усложнения организации, функционирование системы является не просто откликом на изменение внешних условий, а сохранением старого или установлением нового внутреннего равновесия системы. В своих работах Берталанфи исследует общие закономерности, присущие любым достаточно сложным организациям материи как биологической, так и общественной природы. Берталанфи и организованная им школа последователей в своих трудах пытаются придать общей теории систем формальный характер.

Массовое распространение системных представлений, осознание системности мира, общества и человеческой деятельности связано с именем американского математика Н. Винера. В 1948 г. он опубликовал книгу «Кибернетика» [6] и далее «Кибернетика и общество» [7]. В своих трудах он развивает идеи управления и связи в животном мире и машинах, анализирует с позиций кибернетики процессы, происходящие в обществе. Н.Винером и его последователями было указано, что предметом кибернетики является исследование систем. Причем отмечается, что хотя при изучении системы на каком-то этапе потребуется проводить учет ее конкретных свойств, для кибернетики в принципе несущественно, какова природа системы. То есть для изучения систем различных типов, будь она физической, биологической, экономической, организационной или вовсе представленной в виде модели, кибернетика предлагает единые подходы к ее исследованию. Ф.И. Перегудов и Ф.П. Тарасенко в своей книге отмечают, что с кибернетикой Винера связаны такие продвижения в развитии системных представлений как типизация моделей систем, выявление особого значения обратных связей в системе, подчеркивание принципа оптимальности в управлении и синтезе систем, осознание информации как всеобщего свойства материи и возможности ее количественного описания, развитие методологии моделирования вообще и в особенности идеи математического эксперимента с помощью ЭВМ.

Существенное место в развитии кибернетики занимают советские ученые. Можно отметить многочисленные работы академика А. И. Берга. Фундаментальный вклад в развитие кибернетики внес также академик А.Н. Колмогоров. Так в период, когда в Советском Союзе кибернетику считали лженаукой и в стране шли горячие дискуссии о сути кибернетики, были сформулированы достаточно общие и полные определения кибернетики. Приведем эти определения: «Кибернетика — это наука об оптимальном управлении сложными динамическими системами» (А.И. Берг); «Кибернетика - это наука о системах, воспринимающих, хранящих, перерабатывающих и использующих информацию» (А.Н. Колмогоров).

Наконец, отметим достижения в области исследования систем бельгийской школы во главе с И. Пришжиным. Ученые этой школы исследовали механизм самоорганизации систем. Они отмечают, что в результате взаимодействия с окружающей средой система может перейти в неравновесное состояние. В результате такого взаимодействия изменяется организованность системы. Переломные точки, в которых наблюдается неустойчивость неравновесных состояний, называются точками бифуркации. Таким образом, согласно теории И. Пришжина, материя не является пассивной субстанцией, ей присуща спонтанная активность.

Системный анализ как дисциплина сформировался в результате возникновения необходимости исследовать и проектировать сложные системы, управлять ими в условиях неполноты информации, ограниченности ресурсов и дефицита времени. Системный анализ является дальнейшим развитием целого ряда дисциплин, таких как исследование операций, теория оптимального управления, теория принятия решений, экспертный анализ, теория организации эксплуатации систем и т.д. Для успешного решения поставленных задач системный анализ использует всю совокупность формальных и неформальных процедур. Перечисленные теоретические дисциплины являются базой и методологической основой системного анализа. Таким образом, системный анализ - междисциплинарный курс, обобщающий методологию исследования сложных технических, природных и социальных систем. Широкое распространение идей и методов системного анализа, а главное - успешное их применение на практике стало возможным только с внедрением и повсеместным использованием ЭВМ. Именно применение ЭВМ как инструмента решения сложных задач позволило перейти от построения теоретических моделей систем к широкому их практическому применению. В связи с этим Н.Н. Моисеев пишет, что системный анализ - это совокупность методов, основанных на использовании ЭВМ и ориентированных на исследование сложных систем - технических, экономических, экологических и т.д. Центральной проблемой системного анализа является проблема принятия решения. Применительно к задачам исследования, проектирования и управления сложными системами проблема принятия решения связана с выбором определенной альтернативы в условиях различного рода неопределенности. Неопределенность обусловлена многокритериальностью задач оптимизации, неопределенностью целей развития систем, неоднозначностью сценариев развития системы, недостаточностью априорной информации о системе, воздействием случайных факторов в ходе динамического развития системы и прочими условиями. Учитывая данные обстоятельства, системный анализ можно определить как дисциплину, занимающуюся проблемами принятия решений в условиях, когда выбор альтернативы требует анализа сложной информации различной физической природы.

Системный анализ является дисциплиной синтетической. В нем можно выделить три главных направления. Эти три направления соответствуют трем этапам, которые всегда присутствуют в исследовании сложных систем:

1)  построение модели исследуемого объекта;

2)  постановка задачи исследования;

3)  решение поставленной математической задачи.

Рассмотрим данные этапы.

Построение модели (формализация изучаемой системы, процесса или явления) есть описание процесса на языке математики. При построении модели осуществляется математическое описание явлений и процессов, происходящих в системе. Поскольку знание всегда относительно, описание на любом языке отражает лишь некоторые стороны происходящих процессов и никогда не является абсолютно полным. С другой стороны, следует отметить, что при построении модели необходимо уделять основное внимание тем сторонам изучаемого процесса, которые интересуют исследователя. Глубоко ошибочным является желание при построении модели системы отразить все стороны существования системы. При проведении системного анализа, как правило, интересуются динамическим поведением системы, причем при описании динамики с точки зрения проводимого исследования есть первостепенные параметры и взаимодействия, а есть несущественные в данном исследовании параметры. Таким образом, качество модели определяется соответствием выполненного описания тем требованиям, которые предъявляются к исследованию, соответствием получаемых с помощью модели результатов ходу наблюдаемого процесса или явления. Построение математической модели есть основа всего системного анализа, центральный этап исследования или проектирования любой системы. От качества модели зависит результат всего системного анализа.

Постановка задачи исследования. На данном этапе формулируется цель анализа. Цель исследования предполагается внешним фактором по отношению к системе. Таким образом, цель становится самостоятельным объектом исследования. Цель должна быть формализована. Задача системного анализа состоит в проведении необходимого анализа неопределенностей, ограничений и формулировании, в конечном счете, некоторой оптимизационной задачи. Анализируя требования к системе, т. е. цели, которые предполагает достигнуть исследователь, и те неопределенности, которые при этом неизбежно присутствуют, исследователь должен сформулировать цель анализа на языке математики. Язык оптимизации оказывается здесь естественным и удобным, но вовсе не единственно возможным.

Решение поставленной математической задачи. Только этот третий этап анализа можно отнести собственно к этапу, использующему в полной степени математические методы. Хотя без знания математики и возможностей ее аппарата успешное выполнение двух первых этапов невозможно, так как и при построении модели системы, и при формулировании цели и задач анализа широкое применение должны находить методы формализации. Однако отметим, что именно на завершающем этапе системного анализа могут потребоваться тонкие математические методы. Ho следует иметь в виду, что задачи системного анализа могут иметь ряд особенностей, которые приводят к необходимости применения наряду с формальными процедурами эвристических подходов. Причины, по которым обращаются к эвристическим методам, в первую очередь связаны с недостатком априорной информации о процессах, происходящих в анализируемой системе. В данном случае трудности, возникающие в результате необходимости применения неформальных процедур анализа зачастую являются определяющими. Успешное решение задач системного анализа требует использования на каждом этапе исследования неформальных рассуждений. Ввиду этого проверка качества решения, его соответствие исходной цели исследования превращается в важнейшую теоретическую проблему.

Наибольший вклад в формализацию представлений о сложных системах был сделан в связи с развитием автоматизированных систем управления. Авторы работ по теории систем применительно к техническим системам понятие системы формулируют в виде следующих определений.

Под автоматизированной системой понимается программно-аппаратный комплекс, выполненный на базе средств измерительной и вычислительной техники, предназначенный для решения задач управления на основе получения и использования моделей объекта управления. В данном определении констатируется, что автоматизированная система является искусственной системой, создаваемой человеком. Для таких систем конечное состояние или цель функционирования задается заранее, а их поведение направлено на достижение поставленной цели. Цель автоматизированной системы состоит в решении выделенного набора задач автоматизации управления, как правило, поведением технического объекта.

Автоматизированная система - это совокупность частей (технических средств, математических методов, коллектива исполнителей), образующая организационное комплексное единое целое и обеспечивающая решение требуемого набора задач автоматизации с заданной точностью в пределах ограничений во времени и стоимости.

В данном определении уточняется состав элементов, из которых строится система. Также отмечается, что разработка и функционирование системы должны производиться с учетом некоторых ограничений. Иными словами, к системе предъявляются определенные требования оптимальности.

Логичным кажется не искать в литературе всеобъемлющего определения сложной системы, а указать на основные свойства системы, которые всесторонне характеризуют ее и так или иначе присутствуют в различных формулировках определений. Первая существенная особенность системы состоит в том, что система обладает новыми свойствами по сравнению с элементами, из которых она состоит. При этом система есть не просто механический набор элементов, а целенаправленное их соединение в виде определенных структур и взаимосвязей. Система есть организационное единство элементов. Нарушение взаимосвязей приведет к разрушению системы.

Вторая особенность систем состоит в том, что они обладают свойствами оптимальности. Системы проектируются с учетом критериев оптимальности и функционируют согласно построенным заранее оптимальным планам. Следующая черта, которая отражается в определении системы, — это цель или назначение системы. Системы создаются для достижения какой-либо цели, для решения определенных задач. He существует систем, не предназначенных ни для чего, не решающих никаких задач. Любая система имеет свое предназначение.

Подходы к классификации системы могут быть самыми разными:

· по виду отображаемого объекта-технические, биологические, социальные и т. п.;

· по характеру поведения — детерминированные, вероятностные, игровые;

· по типу целеустремленности - открытые и закрытые;

· по сложности структуры и поведения - простые и сложные;

· по виду научного направления, используемого для их моделирования - математические, физические, химические и др.;

· по степени организованности - хорошо организованные, плохо организованные и самоорганизующиеся.

Рассмотрим некоторые из представленных видов классификации. Детерминированной называется система, состояние которой в будущем однозначно определяется ее состоянием в настоящий момент времени и законами, описывающими переходы элементов и системы из одних состояний в другие. Составные части в детерминированной системе взаимодействуют точно известным образом. Примером детерминированной системы может служить механический арифмометр. Установка соответствующих чисел на валике и задание порядка вычисления однозначно определяют результат работы устройства. То же самое можно сказать о калькуляторе, если считать его абсолютно надежным.

Вероятностные или стохастические системы - это системы, поведение которых описывается законами теории вероятностей. Для вероятностной системы знание текущего состояния и особенностей взаимной связи элементов недостаточно для предсказания будущего поведения системы со всей определенностью. Для такой системы имеется ряд направлений возможных переходов из одних состояний в другие, т. е. имеется группа сценариев преобразования состояний системы, и каждому сценарию поставлена в соответствие своя вероятность. Примером стохастической системы может служить мастерская по ремонту электронной и радиотехники. Срок выполнения заказа по ремонту конкретного изделия зависит от количества аппаратуры, поступившей в ремонт до поступления рассматриваемого изделия, от характера повреждений каждого из находящихся в очереди объектов, от количества и квалификации обслуживающего персонала и т. п.

Игровой является система, осуществляющая разумный выбор своего поведения в будущем. В основе выбора лежат оценки ситуаций и предполагаемых способов действий, выбираемых на основе заранее сформированных критериев, а также с учетом соображений неформального характера. Руководствоваться этими соображениями может только человек. Примером игровой системы может служить организация, выполняющая некоторые работы и выступающая в качестве исполнителя. Исполнитель вступает в отношения с заказчиком. Интересы исполнителя и заказчика противоположные. Исполнитель старается продать свою работу как можно выгоднее. Заказчик, наоборот, пытается сбить цену и соблюсти свои интересы. В данном торге между ними проявляется игровая ситуация.

Классификация по данному признаку условна, как и многое другое, касающееся характеристики сложных систем. Она допускает разные толкования принадлежности той или иной системы к сформированным классам. Так в детерминированной системе можно найти элементы стохастичности. С другой стороны, детерминированную систему можно считать частным случаем стохастической системы, если положить вероятности переходов из состояния в состояние соответственно равными нулю (перехода нет) и единице (переход имеет место). Точно также стохастическую систему можно рассматривать как частный случай игровой, когда идет игра с природой.

Следующий признак классификации: открытые и закрытые системы. По данному признаку классификации системы характеризуются различной степенью взаимодействия с внешней средой. Открытые системы обладают особенностью обмениваться с внешней средой массой, энергией, информацией. Замкнутые (или закрытые) системы изолированы от внешней среды. Предполагается, что разница между открытыми и замкнутыми системами определяется с точностью до принятой чувствительности модели.

По степени сложности системы подразделяются на простые, сложные и очень сложные. Простые системы характеризуются небольшим количеством возможных состояний, их поведение легко описывается в рамках той или иной математической модели. Сложные системы отличаются разнообразием внутренних связей, но допускают их описание. Причем набор методов, привлекаемых для описания сложных систем, как правило, многообразен, т. е. для построения математической модели сложной системы применяются различные подходы и разные разделы математики. Очень сложные системы характеризуются большой разветвленностью связей и своеобразностью отношений между элементами. Многообразие связей и отношений таково, что нет возможности все их выявить и проанализировать. Простыми системами можно считать лентопротяжные механизмы, механические передачи, системы слежения за целью и т.д. Сложными системами являются электронно-вычислительная машина, система управления и защиты энергоблока, система электроснабжения промышленного объекта и пр. Очень сложными являются социотехнические системы, такие как автоматизированные системы управления крупным предприятием, экспертные системы с функциями поддержки и принятия управленческих решений.

В системном анализе имеется большая группа задач, в которых требуется спрогнозировать процессы развития системы и принять решение, в результате которого система в будущем должна попасть в некоторое оптимальное состояние. Например, в экономических системах требуется спланировать ассортимент и объем выпускаемой продукции в некоторый будущий период времени с целью получения максимальной прибыли после ее реализации. При этом необходимо спрогнозировать потребность рынка в продукции соответствующего типа, спрос на данный вид продукции. Как уже было отмечено, потребность рынка определяется многими факторами, например, соотношением цены и качества товара, уровнем доходов населения, модой и т.д. При решении задач такого типа на помощь приходит прогностика - наука о способах и методах разработки прогнозов.

Прогнозом называется научно обоснованное суждение об ожидаемых состояниях системы, объекта или явления окружающей действительности.

Прогнозирование - это разработка прогнозов, состоящая в организации и проведении специальных исследований перспектив развития исследуемых объектов, систем или явлений. Научное прогнозирование чаще всего применяется в социально-экономических и научно-технических областях человеческой деятельности. Процесс прогнозирования базируется на изучении объективных тенденций развития объекта исследования. Разработка общей проблемы предсказания должна основываться на изучении реальных закономерностей развития объекта исследования. Содержание и степень достоверности прогноза определяются информацией о поведении объекта исследования, накопленной до того времени, на который составляется прогноз, закономерностями, выявленными при функционировании объекта исследования, а также опытом, знаниями и научной интуицией специалистов, занимающихся данным видом деятельности.

Известны три группы методов прогнозирования, предлагаемых для практического применения, - это методы экстраполяции, методы экспертных оценок и логического моделирования. Методы экстраполяции основаны на аппроксимации результатов, полученных при анализе развития исследуемых процессов, описании полученных данных с помощью математических моделей и дальнейшем расчете моделей для будущих моментов времени. Данные методы позволяют осуществлять поиск приемлемых оценок состояний системы в будущем, однако их применение обоснованно только для описания процессов эволюционного развития. Хотя хорошо известно, что процессы развития систем включают в себя как периоды эволюционного изменения, так и скачкообразные переходы от одних состояний к другим. Скачкообразные переходы обусловлены открытиями новых физических принципов, реализацией оригинальных технических решений, осуществлением крупных проектов. Это обстоятельство должно учитываться при проведении исследований, для чего используются различного рода приемы, позволяющие выделить ожидаемые скачки на общем фоне изменений, интересующих исследователя. Рекомендуемым методом прогнозирования скачкообразных изменений развития систем может быть метод экспертных оценок. При этом в качестве экспертов должны выступать высококвалифицированные в данной области знаний специалисты. Необходимая для формирования прогноза информация обобщается путем обработки мнений экспертов. В результате разрабатывается сценарий развития системы, а также возможные его варианты, учитывающие наличие скачков, предсказание которых особенно ценно для системных аналитиков.

Oсновные процедуры системного анализа:

· изучение структуры системы, анализ ее компонентов, выявление взаимосвязей между отдельными элементами;

· сбор данных о функционировании системы, исследование информационных потоков, наблюдения и эксперименты над анализируемой системой;

· построение моделей;

· проверка адекватности моделей, анализ неопределенности и чувствительности;

· исследование ресурсных возможностей;

· определение целей системного анализа;

· формирование критериев;

· генерирование альтернатив;

· реализация выбора и принятие решений;

· внедрение результатов анализа.

Любая задача системного анализа начинается с построения модели исследуемой системы. Для решения задачи построения модели необходимо вначале произвести изучение структуры системы, выполнить анализ ее компонентов, выявить взаимосвязи между отдельными элементами.

При проведении системного анализа исследователя интересуют вопросы, касающиеся изучения свойств системы. Свойства системы реализуются в процессе ее функционирования, т.е. в процессе динамического поведения системы. Чтобы построить модель системы, которая имела бы возможность отражать свойства и характеристики системы, реализующиеся в процессе ее функционирования во времени, необходимо помимо структуры системы знать ее параметры, поэтому следующим этапом работ при проведении системного анализа является сбор данных о функционировании системы и исследование информационных потоков.

Параметры системы подразделяются на внутренние и внешние.

Внешние параметры системы - характеристики функционирования системы, служащие показателями качества ее работы как единого целого. В качестве примера внешних параметров можно привести параметры автоматизированной системы:

· общая производительность системы по обработке данных;

· объем передаваемой информации;

· достоверность выходной экспериментальной информации;

· точность получения результатов (для информации, заданной количественно);

· количественные характеристики надежности системы;

· объем используемой в системе аппаратуры (объем памяти, количество преобразователей формы информации, количество внешних устройств и т.д.);

· время задержки с момента поступления в систему исходных данных до момента выдачи окончательных результатов (во время решения определенной задачи);

· стоимость системы (с учетом разработки математического обеспечения);

· показатели удобства системы в эксплуатации (наличие элементов «психологического комфорта») и др.

Внутренние параметры системы - характеристики, показывающие особенности технических решений, принятых при организации системы в целом и отдельных технических средств, входящих в состав системы, а также в совокупности влияющие на значения внешних параметров системы. Примерами внутренних параметров автоматизированных систем являются:

· вид и характеристики сигналов для представления информации в системе, в каналах связи - при обмене информацией между отдельными звеньями системы;

· способ кодирования информации;

· вид приоритетности при приеме и обработке информации от различных источников;

· способ организации программы-диспетчера;

· быстродействие отдельных элементов и т.д.

Наблюдения с целью сбора данных могут проводиться в процессе функционирования системы либо же для сбора данных организуются специальные экспериментальные исследования. В первом случае говорят, что данные получены в результате пассивного эксперимента. Во втором случае имеет место активный эксперимент. Активный эксперимент проводится по специально составленному плану с использованием методов планирования эксперимента. При этом предусматривается возможность изменения входных параметров, влияющих на процесс функционирования системы. Исследуется изменение выходных параметров системы в зависимости от уровней входных параметров. Результаты испытаний фиксируются с помощью измерений, т.е. изображения результатов опыта в виде символов, номеров или чисел. Измерение - это алгоритмическая операция, которая данному наблюдаемому состоянию системы или процесса ставит в соответствие определенное обозначение: число, номер или символ. Такое соответствие обеспечивает то, что результаты измерений содержат информацию об исследуемой системе. Требуемая информация в виде оценок параметров получается путем преобразования результатов измерения или, как еще говорят, с помощью статистической обработки экспериментальных данных.

Выделяют два класса моделей: аналитические и имитационные. В аналитических моделях поведение сложной системы записывается в виде некоторых функциональных соотношений или логических условий. Наиболее полное исследование удается провести в том случае, когда получены явные зависимости, связывающие искомые величины с параметрами сложной системы и начальными условиями ее изучения. Однако это удается выполнить только для сравнительно простых систем. Для сложных систем исследователю приходится идти на упрощение реальных явлений, дающее возможность описать их поведение и представить взаимодействия между компонентами сложной системы. Это позволяет изучить хотя бы некоторые общие свойства сложной системы, например, оценить устойчивость системы, характеристики надежности и т.п. Для построения математических моделей имеется мощный математический аппарат (функциональный анализ, исследование операций, теория вероятностей, математическая статистика, теория массового обслуживания и т.д.). Наличие математического аппарата и относительная быстрота и легкость получения информации о поведении сложной системы способствовало повсеместному и успешному распространению аналитических моделей при анализе характеристик сложных систем.

Когда явления в сложной системе настолько сложны и многообразны, что аналитическая модель становится слишком грубым приближением к действительности, системный аналитик вынужден использовать имитационное моделирование. В имитационной модели поведение компонентов сложной системы описывается набором алгоритмов, которые затем реализуют ситуации, возникающие в реальной системе. Моделирующие алгоритмы позволяют по исходным данным, содержащим сведения о начальном состоянии сложной системы, и фактическим значениям параметров системы отобразить реальные явления в системе и получить сведения о возможном поведении сложной системы для данной конкретной ситуации. На основании этой информация аналитик может принять соответствующие решения. Отмечается, что предсказательные возможности имитационного моделирования значительно меньше, чем у аналитических моделей.

Вопрос о том, какой модели следует отдать предпочтение при проведении исследований характеристик системы, не является очевидным. Аналитическая модель имеет некоторые преимущества по сравнению с имитационной моделью. Во-первых, аналитическая модель дает решение поставленной задачи в законченной форме. Во-вторых, применение аналитической модели обеспечивает глубину анализа. С помощью аналитических моделей можно проводить исследование характеристик в некоторой области определения параметров, в которой модель адекватна описываемым явлениям или процессам. Применение аналитических моделей позволяет получить решение в виде функциональной зависимости исследуемых характеристик от параметров модели. Имитационная модель за один цикл ее применения производит расчет характеристик в одной точке. Для получения функциональной зависимости выходной характеристики от параметров модели необходимо провести многократные расчеты на имитационной модели.

С другой стороны, построить аналитическую модель для сложной системы очень трудно. При таком построении требуется принимать существенные упрощающие предположения, которые могут привести к тому, что построенная модель будет неадекватна описываемым процессам или явлениям. В этом смысле имитационные модели имеют преимущества, так как они могут быть построены в самых общих предположениях о функционировании системы. Следовательно, имитационные модели могут быть более адекватны. К недостаткам аналитических моделей относится также и то, что простая модификация проекта или изменение предположений о функционировании элементов структуры может потребовать коренной перестройки модели, в то время как у имитационной модели потребуется изменить лишь входную информацию.

Рассмотрим простой пример. Пусть необходимо оценить характеристики надежности системы, структура которой известна. Если проводить расчеты в предположении об отсутствии восстановительных мероприятий после отказов элементов, то аналитическая модель для такого расчета строится с использованием логико-вероятностного подхода. Если изменить предположения и считать, что после отказа элементов осуществляется восстановление и потоки отказов и восстановлений пуассоновские, то для расчета надежности используются уравнения Колмогорова-Чепмена. Если же будем предполагать восстановление элементов, но потоки отказов или восстановлений описывать не пуассоновским, а каким-нибудь другим распределением, то для построения моделей расчета надежности необходимо использовать аппарат теории восстановления, т.е. для решения одной и той же задачи при смене предположений о характере функционирования системы для построения аналитической модели приходится полностью менять теоретический аппарат. В имитационной модели в этом случае меняются лишь входные данные. Таким образом, на основании сказанного нельзя однозначно решить, какая модель лучше. Обе модели являются полезным инструментом исследования и об их соответствии решаемым проблемам надо судить в контексте конкретного применения. В задачах системного анализа целесообразно проводить комбинированные исследования, использующие как аналитические, так и имитационные модели.

 

Литература: Макрусев В.В. Основы системного анализа [Электронный ресурс]: учебник/— Электрон. текстовые данные.— СПб.: Троицкий мост, 2017.— 248 c. http://www.iprbookshop.ru/70675.html «IPRbooks»

 

Лекция 2. Вероятностное описание событий и процессов. Статистическая обработка экспериментальных данных. Оценивание показателей систем и определение их точности методами математической статистики.

Математическая статистика – это раздел математики, в котором изучаются методы обработки и анализа экспериментальных данных с помощью аппарата теории вероятностей.

Статистической совокупностью называют совокупность предметов или явлений, объединённых каким – либо общим признаком.

Результатом наблюдений над статистической совокупностью являются статистические данные. Обработка статистических данных методами математической статистики приводит к установлению определенных закономерностей, присущих массовым явлениям.

Генеральной совокупностью называется совокупность объектов или явлений, все элементы которой подлежат изучению при статистическом анализе.

В математической статистике генеральная совокупность понимается как совокупность всех мысленных наблюдений, которые могли быть произведены при выполнении данного комплекса условий. Изучение всей генеральной совокупности часто оказывается невозможным, в таком случае рассматривают некоторую часть объёма.

То есть, генеральная совокупность - это множество каких – либо однородных элементов, из которого по определенному правилу выделяется некоторое подмножество – выборка.

Выборочной совокупностью (выборкой) называют множество результатов наблюдений, случайно отобранных из генеральной совокупности. Выборка (случайная) обозначается X = (X ₁, X ₂, … X_n).

Таким образом, выборка представляет собой совокупный результат n независимых наблюдений над некоторой генеральной случайной величиной X.

Величина n –(количество проведенных измерений или наблюдений) называется объёмом выборки.

С точки зрения теории вероятностей, выборка – это n -мерный случайный вектор с одинаково распределёнными независимыми компонентами.

Любая конкретная выборка x = (x ₁, x ₂, … x_n) (её также называют простой выборкой) есть реализация этой совокупности случайных величин.

Выборочное пространство – это пространство, состоящее из реализаций вектора X:

א = { x = (x ₁, x ₂,… x_n)},

где x_i – выборочное наблюдение (i = 1, 2,… n).

Таким образом, понятия выборочного пространства и генеральной совокупности совпадают.

Информация о генеральной совокупности, полученная на основе выборки, всегда будет обладать некоторой погрешностью, так как основывается на изучении только части объектов. Это выдвигает требования к отбору части объектов – выборка должна быть репрезентативной, то есть правильно отражать пропорции генеральной совокупности. Теоретически репрезентативность достигается случайностью отбора, но на практике зачастую прибегают к различным приемам неслучайного отбора. Основой математической статистики будет простая случайная выборка.

Характеристики (параметры) генеральной совокупности, оцененные с помощью выборки, называют выборочными характеристиками, и они, естественно, являются случайными величинами как функции от случайной выборки.

Задачи математической статистики состоят в обоснованном суждении об объективных свойствах генеральной совокупности по результатам случайной выборки (по значениям выборочных характеристик). Решение таких задач требует знания законов распределения выборочных характеристик.

На первом этапе статистической обработки производят ранжирование, то есть упорядочение данных. Упорядоченные по возрастанию числовых значений элементы выборки называют вариационным рядом X ₍₁₎≤ X ₍₂₎≤ …≤ X _{( n )} .

Члены вариационного ряда называют порядковыми статистиками.

Крайние члены: X ₍₁₎ = X_min и X _{( n )} = X_max называют экстремальными значениями    вариационного ряда.

Разность X _{( n )}– X ₍₁₎= X_max – X_min называют размахом выборки.

Промежуток между экстремальными значениями вариационного ряда (X ₍₁₎, X _{( n )}) называют интервалом варьирования.

Если выборочные наблюдения в простой выборке представить в порядке неубывания числовых значений, то получится реализация вариационного ряда х ₍₁₎   ≤ х ₍₂₎ ≤ …≤ х_{( n )}.

При статистическом анализе дискретных случайных величин используют простую таблицу частот.

Если выборка содержит m £ n различных значений и значение х _{( i )} встречается n_i раз, тогда n_i называется частотой, а сам неповторяющейся элемент вариационного ряда х _{( i )} –  варианта.

Если для каждой варианты х _{( i )} указать частоту её появления n_i, то множество пар (х _{( i )}, n_i) называется статистическим рядом.

Статистический ряд для дискретной случайной величины записывают в виде простой таблицы частот.

 

№	значения	частоты
1	x min	n 1
…	…	…
m	x max	nm

Очевидно, что сумма всех частот равна объёму выборки:

.

Если генеральная случайная величина – непрерывная, то её интервал варьированияразбивают на небольшие интервалы, проводя группировку выборочных данных.

Число интервалов группировки m рассчитывают по формуле Стерджеса:

m» 1 + 1,4× ln n,

тогда ширина (или величина) интервала равна

D = ,

где в числителе дроби стоитвариационный размах; x_max – значение X_max; x_min – значение X_min.

Сгруппированные данные записывают в виде таблицы:

№ интервала	Интервал	Частоты
1	(x min, x min + D)	n 1
2	(x min + D, x min + 2× D)	n 2
…	…	…
m	(x max – D x max)	nm

Частота n_i – количество данных, попавших в интервал. Таблицу такого вида называют интервальной. Иногда в интервальной таблице также указывают середины интервалов группировки.

Для графического изображения (представления) выборочных данных используют следующие характеристики: эмпирическую функцию распределения, гистограмму и полигон.

Эмпирическая функция распределения имеет вид: F_n (x) = , где m _n (x) – число элементов выборки, оказавшихся меньше x (– накопленная частота).

Для построения эмпирической функции распределения нанесём на ось OX члены вариационного ряда, затем построим ступенчатую функцию. Высота каждой ступеньки = .

На основе теоремы Бернулли для эмпирической функции распределения можно доказать следующую теорему.   Теорема Гливенко: для любого действительного числа x верно:

F_n (x) F (x),

где F (x) – теоретическая функция распределения, F_n (x)– эмпиричес-кая функция распределения. (В утверждении теоремы имеется в виду поточечная сходимость последовательности функций).

Теорема Колмогорова:         = 0().

То есть, если вокруг эмпирической функции распределения построить узкую зону, то с большой вероятностью можно утверждать, что функция распределения будет лежать в этой зоне.

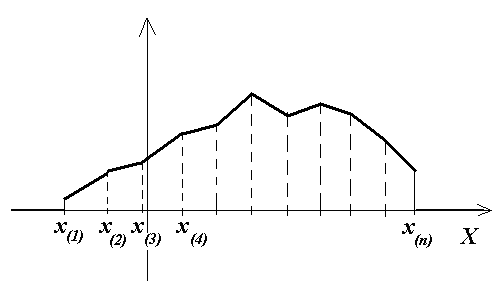Полигон частот – представляет собой ломаную, концы отрезков прямой имеют координаты (x_i; ). Полигон, как правило, служит для графического представления дискретного вариационного ряда. Для интервального ряда тоже строят полигон, только его ломанная проходит через точки, абсциссы которых являются серединами интервалов группировки.

Гистограмма. При построении гистограммы используются сгруппированные данные. По оси OX откладывают интервалы шириной D от х _min до х _max. На каждом интервале строят прямоугольник площадью p_i =   (равной относительной частоте попадания в данный интервал), то есть, высота прямоугольника h_i = 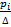. Объединение этих прямоугольников называется гистограммой выборки. Таким образом, площадь каждого прямоугольника гистограммы равна его частоте, а общая площадь равна единице.

С увеличением объема выборки n и уменьшением длины интервала k гистограмма будет приближаться к кривой плотности распределения, поэтому гистограмму используют в качестве оценки для плотности распределения.

Вариационный ряд содержит достаточно полную информацию о генеральной случайной величине X, однако обилие числовых данных, с помощью которых он задаётся, усложняет их использование. На практике достаточно часто оказывается достаточным знание лишь сводных характеристик вариационного ряда: выборочных моментов, моды, медианы, асимметрии и эксцесса.

Расчёт статистических характеристик представляет собой второй после группировки данных этап обработки результатов наблюдений. Рассмотрим основные характеристики.

Выборочная (эмпирическая) средняя: ,

где m – число интервалов группировки, x _{( j )}– соответствующее значение варианты для дискретного случая или середина интервала группировки для непрерывного, n_j – соответствующая частота. В частном случае, когда выборка содержит n различных значений (количество значений равно объёму выборки), все частоты n_j = 1 и формула для выборочного среднего примет более простой вид: .

Выборочная медиана – значение признака, приходящееся на середину вариационного ряда:

Медиану, как меру средней величины, используют в том случае, если крайние члены вариационного ряда по сравнению с остальными, оказались чрезмерно большими или малыми.

Выборочная мода – выборочное значение, которому соответствует наибольшая частота.

Моду можно найти по простой или интервальной таблице частот.

Моду легко найти графическим путем с помощью гистограммы.

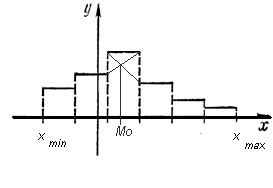
Выборочная дисперсия: S ² = .

Для практических вычислений S ² более удобной является следующая формула:

S ² =` x <sup>2</sup> – (` x)²

(выборочная дисперсия равна разности среднего квадрата и квадрата выборочного среднего), где 

 .

Выборочное среднеквадратическое отклонение есть арифметический квадратный корень из дисперсии S.