Основные положения теории проверки статистических гипотез.

На практике часто приходится проверять на основе выборочных данных различные предположения относительно генеральной совокупности. Процедура сопоставления выдвинутых гипотез с выборкой и вынесения решения относительно приемлемости этих гипотез получила название проверки гипотез.

Такая процедура используется всякий раз, когда необходим обоснованный вывод о преимуществах того или иного способа инвестиций, измерений, стрельбы, технологического процесса, об эффективности нового метода обучения, управления, о пользе удобрений, лекарств, об уровне доходности ценных бумаг, и т.д.

Гипотезой в математической статистике называется любое утверждение о виде или свойствах распределения вероятностей, лежащее в основе наблюдаемых явлений.

По своему содержанию статистические гипотезы можно подразделить на несколько основных типов:

1) гипотезы о числовых значениях параметров случайной величины;

2) гипотезы о виде распределения исследуемой случайной величины;

3) гипотезы об общем виде модели, описывающей статистическую зависимость между случайными величинами.

Проверка статистической гипотезы заключается в том, чтобы оценить, можно ли считать случайным расхождение между выдвинутой гипотезой и результатами выборочного наблюдения. Такая оценка всегда носит вероятностный характер.

Если расхождение между эмпирическими и теоретическими значениями не выходит на пределы случайной ошибки, то можно считать, что с заданной вероятностью выдвинутая гипотеза не опровергается.

При этом справедливость самой гипотезы не доказывается, а лишь делается вывод о том, можно ли считать её допустимой или необходимо опровергнуть.

Гипотезы подразделяют на параметрические и непараметрические, простые и сложные.

Гипотеза называется параметрической, если в ней содержится некоторое утверждение о значении параметра распределения известного вида.

В непараметрической гипотезе заключается утверждение обо всём распределении.

Простая гипотеза полностью определяет теоретическую функцию распределения.

Сложная гипотеза определяет область возможных значений исследуемого параметра.

Например, гипотеза «вероятность успеха в одном испытании Бернулли равна ½» - простая; гипотеза «вероятность успеха в одном испытании Бернулли меньше, чем ½» - сложная.

Обычно выделяют некоторую основную (нулевую) гипотезу Н₀. Наряду с ней рассматривают конкурирующую (альтернативную) гипотезу Н₁, являющуюся логическим отрицанием основной.

Статистический критерий – это правило, по которому нужно принять или опровергнуть выдвинутую гипотезу.

Т.о. статистический критерий представляет собой такое правило, по которому устанавливается, при каких результатах выборочного обследования основная гипотеза не может быть отклонена, а при каких от неё необходимо отказаться.

Суть проверки статистической гипотезы заключается в следующем: используется специально составленная статистика (некоторая функция от выборки), точное или приближенное распределение которой известно. Множество возможных значений статистики делится на две взаимно дополняющих области:

W - область отклонения выдвинутой гипотезы или критическая область критерия;

 - область принятия гипотезы или область допустимых значений статистики.

При этом возможны 4 случая:

Основная гипотеза	Принимается	Отвергается
Верна	Правильное решение	Ошибка I-го рода
Неверна	Ошибка II-го рода	Правильное решение

Вероятности ошибок I и II рода однозначно определяются выбором критической области.

Будем обозначать вероятность ошибки I-го рода через a. Вероятность ошибки II-го рода обозначим b.

Применяя юридическую терминологию, можно интерпретировать величины a и b следующим образом:

a - вероятность вынесения судом обвинительного приговора, когда на самом деле обвиняемый невиновен;

b - вероятность вынесения судом оправдательного приговора, когда на самом деле обвиняемый виновен.

Вероятность a отвергнуть гипотезу, когда она верна, называют уровнем значимости критерия, т.е. это вероятность совершить ошибку I-го рода.

Обычно уровень значимости a принимают равным 0,05; 0,01; 0,005; 0,001.

Вероятность 1- b отвергнуть гипотезу, когда она не верна, т.е. не допустить ошибку II-го рода, называются мощностью критерия.

Уменьшая уровень значимости a, мы снижаем вероятность появления ошибки первого рода. Однако, если основная гипотеза не верна, то, уменьшая a, мы увеличиваем область допустимых значений и, соответственно, вероятность появления ошибки второго рода b.

Стремление увеличить мощность критерия 1- b при неизменном объёме выборки приводит к расширению критической области, то есть повышает вероятность ошибки первого рода a.

Одновременно уменьшить вероятности a и b можно, лишь увеличивая объём выборки n.

Если же объём выборки фиксирован, то при равных a выбирают тот критерий, где меньше b. То есть критическая область критерия должна быть такой, чтобы при заданном уровне значимости a мощность критерия 1- b была максимальной.

Задача построения наиболее мощного критерия для простой гипотезы решается с помощью леммы Неймана – Пирсона:

 Среди всех критериев заданного уровня значимости a, проверяющих простую гипотезу Н₀ против альтернативы Н₁, критерий отношения правдоподобия является наиболее мощным.

Рассмотри применение этой леммы.

 Так как гипотеза является простой, то можно однозначно определить функцию правдоподобия при основной и альтернативной гипотезах:

; .

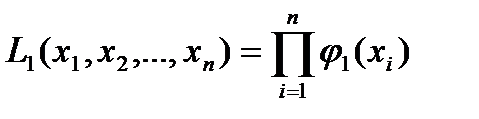Чем правдоподобнее выборка в условиях гипотезы Н₁, тем больше L ₁ по сравнению с L ₀, следовательно больше отношение L ₁ / L ₀. В качестве критической области выбирают область больших значений ln [ L ₁ / L ₀ ].

Границу критической области вычисляют исходя из конкретного вида распределения и заданного уровня значимости. Построенный таким образом (по лемме Неймана – Пирсона) критерий будет наиболее мощным.

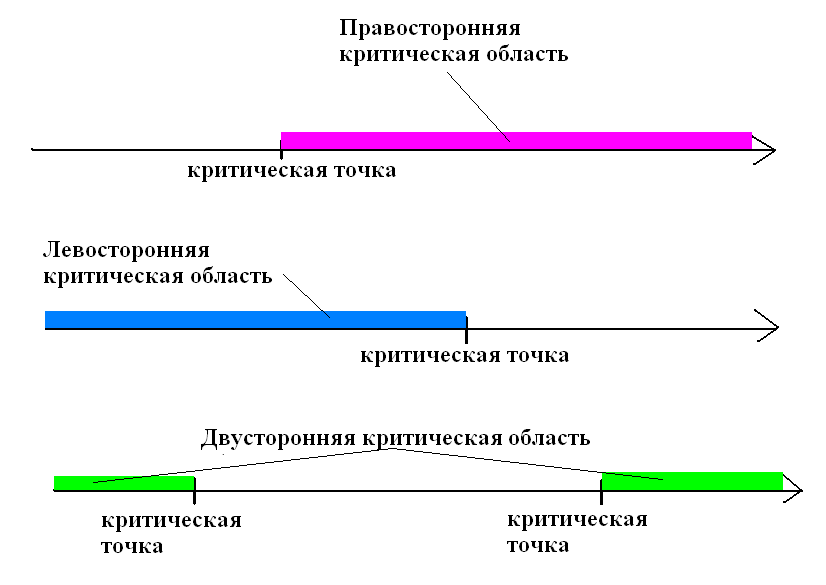
Точка, разделяющая критическую область и область принятия нулевой гипотезы, называется критической.

При заданном уровне значимости критическая область (т.е. область отклонения выдвинутой гипотезы) может быть односторонняя (правосторонняя, левосторонняя) или двусторонняя в зависимости от вида альтернативной гипотезы

 

Общий порядок проверки статистических гипотез.

1. Формулируется основная (проверяемая) и альтернативная гипотезы.

2. Выбирается статистический критерий для проверки справедливости основной гипотезы.

3. Определяются критическая область и область допустимых значений, значения статистики критерия в критических точках

4. По результатам статистического исследования подсчитывается фактическое значение статистики критерия.

5. На основе сравнения фактического и критического значений статистики критерия делается вывод о правдоподобности или необходимости отклонения выдвинутой гипотезы.

Схема проверки статистической гипотезы не даёт точного вывода о её верности или неверности, так как принятие гипотезы всегда происходит на некотором субъективно принятом уровне надёжности и основывается на значении статистики, построенной по конечной выборке.

Принятие основной гипотезы не означает, что она является единственно подходящей, просто она не противоречит выборочным данным. Однако таким же свойством могут обладать и другие гипотезы.