Лекция 2Векторы.
Rn – это множество, элементами которого являются упорядоченные наборы из n чисел (а1, а2, …, аn) =` a, которые будем называть “векторами”.
В Rn определены операции: сложение векторов и произведение векторов на числоаналогично матричным операциям..
Определение 2.1. Линейной комбинацией векторов
` а1, ` а 2, ¼, ` а n с коэффициентами l 1, l 2, ¼, l n называется вектор
`b = l 1 ` a 1 + l 2 ` a 2 + ¼ + l n ` a n.
Определение2.2. Система векторов {` а1, ` а 2, ¼, ` а n } называется линейно зависимой, если хотя бы один из векторов этой системы есть линейная комбинация остальных. В противном случае она называется линейно независимой (то есть ни один из векторов данной системы нельзя представить в виде линейной комбинации остальных).
Определение 2.3. Совокупность элементов B = {` b 1, ` b 2, ¼, ` b n }Ì Rn
называется базисом в Rn, если любой элемент ` х Î Rn можно единственным образом представить в виде:
` х = х1 ` b1 + х2 ` b2 + …+ хn ` bn, xi Î Rn; i = 1, 2, …, n. Коэффициенты  разложения вектора
разложения вектора  по базису называются координатами вектора
по базису называются координатами вектора  относительно данного базиса
относительно данного базиса
Критерий базиса. Для того, чтобы система В была базисом в Rn необходимо и достаточно, чтобы ∆ (` b 1, ` b 2, ¼, ` b n) ≠ 0.
Естественный базис в Rn образуют векторы
` е1 = (1, 0, 0,…, 0); ` е2 = (0, 1, 0,…, 0); … ` еn = (0, 0, 0,…, 1)
Определение 2.4. Скалярным произведением векторов
 и
и  называется число
называется число  равное сумме произведений одноименных координат:
равное сумме произведений одноименных координат: 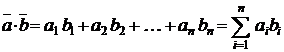 .
.
Свойства скалярного произведения
1.  (коммутативность);
(коммутативность);
2. 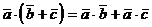 (дистрибутивность);
(дистрибутивность);
3. 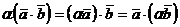 (ассоциативность по отношению к умножению на число);
(ассоциативность по отношению к умножению на число);
4. 
Норма вектора в Rn
Определение 2.5. Нормой вектора  в Rn называют число
в Rn называют число
 .
.
Свойства нормы вектора
1. Для любого 
 , причем
, причем 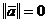 тогда и только тогда, когда
тогда и только тогда, когда  .
.
2. Для любого 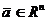 и числа
и числа  .
.
3. Для любых  справедливо неравенство треугольника:
справедливо неравенство треугольника:  .
.
Определение 2.6. Если векторы  и
и 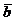 ненулевые, то углом между ними называется число
ненулевые, то углом между ними называется число 
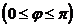 , вычисляемое из соотношения:
, вычисляемое из соотношения:
 . .
|
Определение 2.7. Вектора  и
и 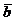 из
из  называются ортогональными, если
называются ортогональными, если 
Два ненулевые вектора в  (или в
(или в  ) ортогональны тогда и только тогда, когда угол между ними равен
) ортогональны тогда и только тогда, когда угол между ними равен 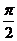 , то есть когда эти векторы перпендикулярны.
, то есть когда эти векторы перпендикулярны.
 |  | ||
Векторное произведение в R3.




 C
C
 |
Определение 2.8. Векторным произведением вектора ` а на ` b в R3 называется вектор` с (см. рисунок):
а) норма которого численно равна площади параллелограмма, построенного на векторах ` а и ` b, как на сторонах;
б) вектор ` с перпендикулярен к плоскости параллелограмма;
 |
в) направлен так, что кратчайшее вращение вектора` а к вектору ` b мы
наблюдаем с конца вектора ` с совершающимся против часовой стрелки (говорят также, что (` а, ` b, ` c) – правая связка).
Векторное произведение обозначают ` с = ` а ´ ` b.
Теорема. (Выражение векторного произведения через координаты векторов).
Если ` a = (а1, а2, а3), ` b = (b1, b2 , b3), то ` a ´ ` b вычисляется по формуле: 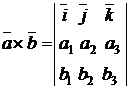
где ` i, ` j, ` k образуют естественный базис в R3:  .
.
Свойства векторного произведения
1. 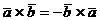 (антикоммутативность);
(антикоммутативность);
2.  (дистрибутивность);
(дистрибутивность);
3.  ;
;
4. 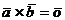 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  и
и 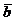 линейно зависимы.
линейно зависимы.






