 .
.
Из чертежа (рис. 1)

и число зон
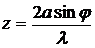 (1)
(1)
При четном числе зон, то есть при
 где
где 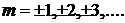 (2)
(2)
имеем минимум интенсивности. Приравнивая выражения (1) и (2) получаем условие минимума:
 (3)
(3)
Целое число  определяет порядок минимума. Первый минимум имеет место при
определяет порядок минимума. Первый минимум имеет место при  , то есть в том направлении, для которого в щели укладывается четыре зоны, и т.д.
, то есть в том направлении, для которого в щели укладывается четыре зоны, и т.д.
Максимум интенсивности наблюдается при нечетном числе зон, то есть при
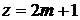 , (4)
, (4)
где  .
.
Из выражений (1) и (4) получим условие максимума:
 , (5)
, (5)
где  .- порядок дифракционного максимума.
.- порядок дифракционного максимума.
Первый максимум получим при  , то есть когда в щели укладывается три зоны; затем – при
, то есть когда в щели укладывается три зоны; затем – при  (пять зон) и т.д.
(пять зон) и т.д.
На экране дифракционная картина имеет следующий вид. В центре экрана имеет место центральный максимум (точка О), в которой интерферируют лучи, идущие под углом  . Для этих лучей разность хода равна нулю, и они усиливают друг друга. По обе стороны от центрального максимума чередуются темные и светлые полосы соответствующего цвета падающей длины волны
. Для этих лучей разность хода равна нулю, и они усиливают друг друга. По обе стороны от центрального максимума чередуются темные и светлые полосы соответствующего цвета падающей длины волны 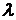 .
.
Если на щель падает белый свет, то центральный максимум представляет яркую белую полоску, так как в точке О условие максимума выполняется для всех длин волн. Боковые максимумы спектральные, обращенные фиолетовой полосой к центральному. Это следует из того, что по условию максимума (5)  ~
~ 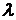 , то есть для меньшей длины волны угол
, то есть для меньшей длины волны угол  меньше для наблюдения максимума любого порядка.
меньше для наблюдения максимума любого порядка.
2. Дифракционная решетка.
Одномерная дифракционная решетка представляет собой систему параллельных щелей одинаковой ширины  , лежащих в одной плоскости и разделенных непрозрачными промежутками равной ширины
, лежащих в одной плоскости и разделенных непрозрачными промежутками равной ширины 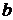 (рис. 2). Величина
(рис. 2). Величина  называется постоянной, или периодом дифракционной решетки.
называется постоянной, или периодом дифракционной решетки.
 Если на дифракционную решетку падает плоский фронт монохроматической волны перпендикулярно ее плоскости, то после прохождения решетки, согласно принципу Гюйгенса – Френеля, вторичные волны от щелей решетки распространяются по всем возможным направлениям и при наложении интерферируют. Помещая на пути распространения волн, идущих за решеткой, собирающую линзу Л, на экране Э, находящемся в фокальной плоскости линзы, наблюдается дифракционная картина: чередование светлых и темных полос.
Если на дифракционную решетку падает плоский фронт монохроматической волны перпендикулярно ее плоскости, то после прохождения решетки, согласно принципу Гюйгенса – Френеля, вторичные волны от щелей решетки распространяются по всем возможным направлениям и при наложении интерферируют. Помещая на пути распространения волн, идущих за решеткой, собирающую линзу Л, на экране Э, находящемся в фокальной плоскости линзы, наблюдается дифракционная картина: чередование светлых и темных полос.
В случае дифракционной решетки условия максимума и минимума иные, чем при дифракции на одной щели, так как при прохождении света через систему щелей имеет место дополнительная интерференция волн.
Очевидно, что направление  , в котором одна щель дает дифракционный минимум, будет направлением ослабления света и для всей системы щелей. Эти главные минимумы интенсивности света наблюдаются в направлениях, определяемых условием (3):
, в котором одна щель дает дифракционный минимум, будет направлением ослабления света и для всей системы щелей. Эти главные минимумы интенсивности света наблюдаются в направлениях, определяемых условием (3):


Если в направлении  одна щель дает усиление интенсивности света (максимум), то вся система щелей в этом направлении может дать либо усиление, либо ослабление интенсивности света. В этом случае необходимо рассматривать условия интерференции соответственных лучей.
одна щель дает усиление интенсивности света (максимум), то вся система щелей в этом направлении может дать либо усиление, либо ослабление интенсивности света. В этом случае необходимо рассматривать условия интерференции соответственных лучей.
Соответственными лучами называются параллельные лучи, идущие под углом  к первоначальному направлению от соответствующих точек щелей, находящихся на расстоянии
к первоначальному направлению от соответствующих точек щелей, находящихся на расстоянии  друг о друга (лучи 1, 2, 3 и т.д. на рис. 2).
друг о друга (лучи 1, 2, 3 и т.д. на рис. 2).
Результат интерференции любой пары соответственных лучей определяется их разностью хода. Из чертежа (рис. 2) для лучей 2 и 3 разностью хода является отрезок | 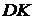 |, равный:
|, равный:
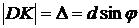 . (6)
. (6)
Если в разности хода укладывается целое число длин волн 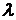 (
( ), то эти соответственные лучи усиливают друг друга. Таким образом, это условие главных дифракционных максимумов определяется соотношением:
), то эти соответственные лучи усиливают друг друга. Таким образом, это условие главных дифракционных максимумов определяется соотношением:
 ,
, 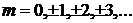 (7)
(7)
Если в разности хода соответственных лучей укладывается нечетное число длин полуволн  (
( ), то эти лучи гасят друг друга, то есть в этом направлении возникают дополнительные минимумы. Их условием является соотношение:
), то эти лучи гасят друг друга, то есть в этом направлении возникают дополнительные минимумы. Их условием является соотношение:
 ,
,  (8)
(8)
Целое число  называется порядком спектра дифракционного минимума или максимума.
называется порядком спектра дифракционного минимума или максимума.
Из условия (7) при  получаем положение центрального максимума, имеющего нулевой порядок. При
получаем положение центрального максимума, имеющего нулевой порядок. При  условие (7) определяет угол
условие (7) определяет угол  , в направлении которого наблюдаются максимумы первого порядка, расположенные вправо и влево от центрального максимума, и т.д. Таким образом, в фокальной плоскости линзы Л на экране Э наблюдается следующая дифракционная картина: центральная наиболее яркая и узкая полоса и ряд постепенно убывающих по яркости полос, симметрично расположенных относительно центральной.
, в направлении которого наблюдаются максимумы первого порядка, расположенные вправо и влево от центрального максимума, и т.д. Таким образом, в фокальной плоскости линзы Л на экране Э наблюдается следующая дифракционная картина: центральная наиболее яркая и узкая полоса и ряд постепенно убывающих по яркости полос, симметрично расположенных относительно центральной.
При освещении дифракционной решетки белым светом, как и в случае одной щели, на экране наблюдаются дифракционные спектры. Центральный максимум нулевого порядка представляет яркую белую полосу, так как из формулы (7) видно, что  соответствует максимуму при
соответствует максимуму при  для всех длин волн
для всех длин волн 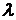 . Поскольку
. Поскольку  ~
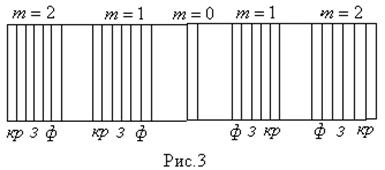
~ 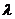 , то все остальные максимумы расположены в спектральной полосе влево и вправо от центрального и обращены фиолетовой частью (наименьшая длина волны) к центру (рис. 3).
, то все остальные максимумы расположены в спектральной полосе влево и вправо от центрального и обращены фиолетовой частью (наименьшая длина волны) к центру (рис. 3).
Зная период дифракционной решетки  и измеряя экспериментально угол
и измеряя экспериментально угол  и порядок спектра
и порядок спектра  , из формулы (7) можно вычислить длину волны
, из формулы (7) можно вычислить длину волны 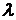 :
:
 . (9)
. (9)
Таким образом, задача определения длины волны 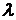 с помощью дифракционной решетки сводится к измерению углов
с помощью дифракционной решетки сводится к измерению углов  , в направлении которых наблюдаются максимумы m -го порядка для выбранной длины волны.
, в направлении которых наблюдаются максимумы m -го порядка для выбранной длины волны.
Описание установки
В данной работе измерения производятся с помощью гониометра (рис.4), который позволяет наблюдать дифракционную картину от одномерной решетки и измерять углы  .
.

Прибор состоит из зрительной трубы 7, коллиматора 10, основания 2 с осевой системой и столиком 9. Зрительная трубка и коллиматор 10 имеют аналогичную конструкцию. Окулярные устройства крепятся к трубам с помощью колец 6 и 12. Коллиматор 10 показан с раздвижной щелью 11. Лимб гониометра и сетки окуляров освещаются лампой в подсветке 3. Прибор включается в сеть переменного тока общим выключателем. Зрительная труба 7 со стойкой крепится к алидаде 8.
Коллиматор 10 установлен на стойке 1, которая закреплена неподвижно на основании 2. Для получения и исследования явления дифракции перед щелью 11 ставится осветитель, а на столике 9 гониометра устанавливается дифракционная решетка так, чтобы ее плоскость была перпендикулярна оси коллиматора 10. Зрительная труба 7 при помощи системы линз собирает в фокальной плоскости объектива параллельные пучки света, идущие от дифракционной решетки. В окуляре зрительной трубы наблюдается дифракционная картина.
В центре поля зрения окуляра в зрительной трубе на том месте, где лежит действительное изображение щели коллиматора, находится тонкая нить. При отсчете углов  изображение дифракционной полосы и нити совмещается.
изображение дифракционной полосы и нити совмещается.
Рассмотрим, как производится отсчет углов в данной установке. Гониометр имеет угловое отчетное устройство. Окуляр 5 отчетного устройства расположен под окуляром зрительной трубы 7. С помощью окуляра 5 мы видим изображение двух диаметрально противоположных участков стеклянного лимба. Изображения штрихов двух диаметрально противоположных участков лимба через систему призм и объективов передаются в оптический микрометр, причем одно изображение прямое, другое - обратное.
 На поверхности лимба нанесена шкала с делениями. Лимб разделен на 1080 делений. Цена деления 20′. Оцифровка делений произведена через 10. При перемещении шкалы на 600 делений верхнее изображение штрихов лимба смещается относительно нижнего на 10′. Каждое деление шкалы соответствует 1/600 от угла 10′, т.е. углу, равному 1′′.
На поверхности лимба нанесена шкала с делениями. Лимб разделен на 1080 делений. Цена деления 20′. Оцифровка делений произведена через 10. При перемещении шкалы на 600 делений верхнее изображение штрихов лимба смещается относительно нижнего на 10′. Каждое деление шкалы соответствует 1/600 от угла 10′, т.е. углу, равному 1′′.
Поле зрения отсчетного микроскопа приведено на рис. 5. В левом окне наблюдается изображение диаметрально противоположных участков лимба и вертикальный индекс для отсчета градусов, а в правом окне делений шкалы – деления шкалы оптического микрометра и горизонтальный индекс для отсчета минут и секунд. Чтобы снять отсчет по лимбу, необходимо повернуть маховичок 4 оптического микрометра настолько, чтобы верхние и нижние изображения штрихов лимба в левом окне точно совместились.
Число градусов будет равно видимой ближайшей левой от вертикального индекса цифре 0. Число десятков минут равно числу интервалов, заключенных между верхним штрихом, который соответствует отсчитанному числу градусов, и нижним оцифрованным штрихом, отличающимся от верхнего на 1800. На рис. 5 число десятков минут равно единице.
Число единиц минут отсчитывается по шкале микрометра в правом окне по левому ряду чисел. На рис. оно равно 5. Число десятков секунд – в том же окне по первому ряду чисел. Число единиц секунд равно числу делений между штрихами, соответствующими отсчету десятков секунд, и неподвижным горизонтальным индексом. Положение, показанное на рис. 5, соответствует отсчету 0015′57′′.
Порядок выполнения работы
1. Поместить перед щелью коллиматора источник света, совместить нить в зрительной трубе с изображением щели.
2. Установить дифракционную решетку в центре столика гониометра так, чтобы штрихи решетки были параллельны щели, а плоскость решетки перпендикулярна оптической оси коллиматора.
3. Изучить дифракционную картину, полученную от дифракционной решетки. Для этого зрительную трубу нужно вращать рукой и в окуляр трубы наблюдать картину. Подсчитать, сколько порядков спектров наблюдается.
4. Повернуть зрительную трубу влево, навести нить трубы на первый дифракционный максимум ( ) определенной длины волны и замерить показания лимба
) определенной длины волны и замерить показания лимба  .
.
5. Проделать такие измерения для трех длин волн (фиолетовой, зеленой, красной) для максимумов первого и второго порядков.
6. Вычислить значение длины волны по формуле
 ,
,
где  - период дифракционной решетки;
- период дифракционной решетки;  - порядок спектра.
- порядок спектра.
7. Данные измерений и вычислений занести в таблицу.
8. Сравнить полученные значения с табличными данными.
Таблица измерений и вычислений
| Линия | 
| 
| 
| 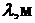
| 
|
| Фиолетовая | 1 2 | ||||
| Зеленая | 1 2 | ||||
| Красная | 1 2 |
Контрольные вопросы
1. Что называется явлением дифракции.
2. Сформулировать принцип Гюйгенса-Френеля.
3. В чем суть метода зон Френеля.
4. Вывести условия максимумов и минимумов для дифракции на одной щели.
5. Вывести условие главных дифракционных максимумов для дифракционной решетки.
6. Чем отличается дифракционная картина при освещении дифракционной решетки монохроматическим и белым светом? Почему?
7. Какой вид имеет центральная дифракционная полоса и почему?
8. Какие измерения нужно сделать в данной работе.
9. Вывести расчетную формулу длины волны.
Лабораторная работа № 5






