Энергетической характеристикой световой волны в данной точке пространства является интенсивность света  .
.
Интенсивностью света  в данной точке пространства называется модуль среднего по времени значения плотности потока энергии, переносимой электромагнитной волной.
в данной точке пространства называется модуль среднего по времени значения плотности потока энергии, переносимой электромагнитной волной.
Плотность потока электромагнитной энергии определяется вектором Умова – Пойтинга:
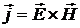 .
.
Следовательно, 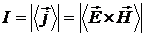 . Единица измерения интенсивности
. Единица измерения интенсивности  .
.
Из теории электромагнитных волн вытекает, что интенсивность света пропорциональна показателю преломления среды и квадрату амплитуды световой волны:

 для
для  ,
,  (3)
(3)
Световая энергия распространяется вдоль линии, называемой лучом. В изотропных средах лучи перпендикулярны волновым поверхностям.
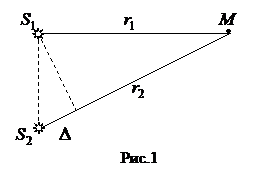
Пусть две световые волны, исходящие из когерентных источников 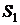 и
и  (рис. 1), приходят в точку М. В этой точке волны, накладываясь друг на друга, возбуждают колебания одинакового направления.
(рис. 1), приходят в точку М. В этой точке волны, накладываясь друг на друга, возбуждают колебания одинакового направления.
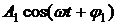 и
и  .
.
Амплитуда результирующего колебания в точке М определяется выражением:
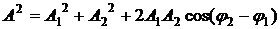 . (4)
. (4)
Так как волны когерентны, то  имеет постоянное во времени значение для данной точки М. Для любой другой точки пространства
имеет постоянное во времени значение для данной точки М. Для любой другой точки пространства  тоже имеет постоянное во времени, но другое свое значение. Таким образом, результат интерференции в любой точке пространства определяется разностью фаз
тоже имеет постоянное во времени, но другое свое значение. Таким образом, результат интерференции в любой точке пространства определяется разностью фаз  , с которой две когерентные волны приходят в данную точку.
, с которой две когерентные волны приходят в данную точку.
 Для простоты и не в ущерб излагаемому материалу предположим, что начальные фазы волн, испускаемых источниками
Для простоты и не в ущерб излагаемому материалу предположим, что начальные фазы волн, испускаемых источниками 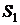 и
и  равны нулю. Тогда уравнения волн в точке М запишутся соответственно:
равны нулю. Тогда уравнения волн в точке М запишутся соответственно:
 и
и
 .
.
Фазы этих волн  и
и 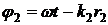 , где
, где  и
и  - расстояние от источников
- расстояние от источников 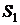 и
и  до точки М.
до точки М.
Разность фаз ( . Волновое число
. Волновое число  можно выразить через другие характеристики волны.
можно выразить через другие характеристики волны.
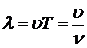 ,
,
где 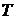 - период,
- период,  - линейная частота,
- линейная частота,  - фазовая скорость волны.
- фазовая скорость волны.
 ,
,
так как  - абсолютный показатель преломления среды. Тогда
- абсолютный показатель преломления среды. Тогда
 . (5)
. (5)
Величина  называется оптическим ходом луча. Таким образом:
называется оптическим ходом луча. Таким образом:  - оптическая разность хода. Формулу (5) можно переписать следующим образом:
- оптическая разность хода. Формулу (5) можно переписать следующим образом:
 , (6)
, (6)
где  - длина световой волны в вакууме.
- длина световой волны в вакууме.
Согласно формуле (4) значение амплитуды  результирующего колебания зависит от значения
результирующего колебания зависит от значения  и принимает различные значения в разных точках пространства. Наибольшее значение амплитуда принимает в тех точках пространства, для которых
и принимает различные значения в разных точках пространства. Наибольшее значение амплитуда принимает в тех точках пространства, для которых 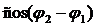 =+1. Это имеет место, если аргумент
=+1. Это имеет место, если аргумент
 , где
, где  - целое число. (7)
- целое число. (7)
Сравнивая выражения (6) и (7), получим:
 - условие максимума интерференции. (8)
- условие максимума интерференции. (8)
Если в разности хода  двух лучей, приходящих в данную точку пространства, укладывается четное число полуволн (или целое число волн), то в этой точке наблюдается интерференционный максимум.
двух лучей, приходящих в данную точку пространства, укладывается четное число полуволн (или целое число волн), то в этой точке наблюдается интерференционный максимум.
При этом 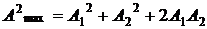 , или
, или  . Интенсивность света
. Интенсивность света
 .
.
В случае равенства амплитуд 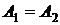 (или, что тоже самое, равенства интенсивностей
(или, что тоже самое, равенства интенсивностей 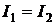 )
)
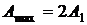 и
и 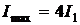 .
.
Соответственно наименьшее значение амплитуда результирующего колебания принимает в тех точках пространства, для которых  . Это имеет место, если аргумент
. Это имеет место, если аргумент
 ,где
,где 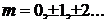 - целое число. (9)
- целое число. (9)
Вновь из выражений (6) и (9) получим
 - условие минимума интерференции. (10)
- условие минимума интерференции. (10)
Если в разности хода 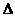 двух лучей, приходящих в данную точку пространства, укладывается нечетное число полуволн, то в этой точке наблюдается интерференционный минимум.
двух лучей, приходящих в данную точку пространства, укладывается нечетное число полуволн, то в этой точке наблюдается интерференционный минимум.
При этом  или
или  .
.
Интенсивность света  . В случае равенства амплитуд
. В случае равенства амплитуд  (или интенсивностей
(или интенсивностей 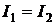 )
)  и
и  . Эти точки пространства будут темными.
. Эти точки пространства будут темными.
Отметим, что согласно закону сохранения энергии при интерференции происходит такое распределение энергии, что усиление интенсивности света в одних точках пространства осуществляется за счет ослабления в других.
При наложении некогерентных волн разность фаз (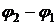 ) слагаемых колебаний в любой точке пространства изменяется с течением времени хаотически и
) слагаемых колебаний в любой точке пространства изменяется с течением времени хаотически и 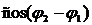 изменяется тоже хаотически от +1 до –1. Среднее во времени значение косинуса равно нулю. Тогда квадрат амплитуды суммарного колебания согласно формуле (4):
изменяется тоже хаотически от +1 до –1. Среднее во времени значение косинуса равно нулю. Тогда квадрат амплитуды суммарного колебания согласно формуле (4):

и соответственно интенсивность  одинакова для всех точек пространства, то есть интерференция наблюдаться не будет, так как не происходит перераспределения энергий света в пространстве.
одинакова для всех точек пространства, то есть интерференция наблюдаться не будет, так как не происходит перераспределения энергий света в пространстве.
Источником световых волн являются возбужденные атомы вещества. Каждый атом излучает электромагнитные волны независимо друг от друга и поэтому начальные фазы излучаемых волн различны и непрерывно меняются со временем. Создать два независимых когерентных источника света трудно. Практически все методы получения когерентных световых волн сводятся к разделению световой волны от одного источника на две волны, которые являются когерентными. Затем эти волны, накладываясь друг на друга, интерферируют между собой.
Одним из оптических устройств получения когерентных световых волн и наблюдения интерференции света является бипризма Френеля, которая используется в данной работе.
Бипризма Френеля состоит из двух одинаковых призм с малыми (порядка  ) преломляющими углами А и В, сложенных основаниями и изготовленных как одно целое (рис. 2).
) преломляющими углами А и В, сложенных основаниями и изготовленных как одно целое (рис. 2).

Свет из узкой щели S проходит через бипризму и в результате преломления за бипризмой получаются сходящиеся пучки света, которые можно рассматривать как исходящие из мнимых источников S 1 и S 2. Поскольку оба пучка света исходят от одного источника, то они когерентны, и поэтому, накладываясь друг на друга за бипризмой, интерферируют между собой. Интерференционная картина на экране MN представляет чередование темных и светлых полос, параллельных щели S.
Расстояние между двумя соседними светлыми (или темными) полосами называется шириной интерференционной полосы. Ширина интерференционной полосы на экране изменяется в зависимости от расстояния между источниками света и экраном.
Для вывода расчетной формулы рассмотрим рис. 3, где S 1 и S 2 – когерентные источники света, расположены на расстоянии d друг от друга.
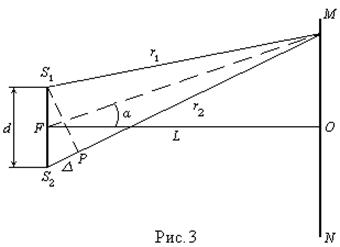
Интерференционная картина наблюдается на экране, расположенном от источников S 1 и S 2 на расстоянии | FO | = L >> d. Считая, что лучи S 1 М и S 2 М распространяются в одинаковой среде, определим их разность хода 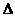 = | S 2 P | =
= | S 2 P | =  , с которой они приходят в точку М, отстоящую от центра экрана О на расстоянии
, с которой они приходят в точку М, отстоящую от центра экрана О на расстоянии  | OM | << L. Острый угол
| OM | << L. Острый угол 
 S 2 S 1 P определяется преломляющим углом бипризмы и, следовательно, мал. А так как
S 2 S 1 P определяется преломляющим углом бипризмы и, следовательно, мал. А так как  <<
<< 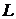 и
и  <<
<< 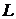 , то угол OFM также равен
, то угол OFM также равен  , а треугольники S 2 S 1 P и OFM можно считать подобными. Из подобия этих треугольников получим:
, а треугольники S 2 S 1 P и OFM можно считать подобными. Из подобия этих треугольников получим:
 , откуда
, откуда  . (11)
. (11)
Подставляя в формулу (11) условие максимума (8) или минимума (10), получим положение светлых и темных полос на экране.
Если 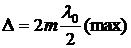 , то получим усиление света, то есть светлую полосу, положение которой
, то получим усиление света, то есть светлую полосу, положение которой
 , где
, где 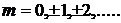 . (12)
. (12)
Целое число  определяет порядок интерференционного максимума.
определяет порядок интерференционного максимума.
Если  , то
, то 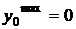 , то есть в центре экрана получим центральный максимум, в центре экрана лучи всегда сходятся в одинаковой фазе. Максимум первого порядка находится на расстоянии
, то есть в центре экрана получим центральный максимум, в центре экрана лучи всегда сходятся в одинаковой фазе. Максимум первого порядка находится на расстоянии
 .
.
Если  , то получим ослабление света, то есть темную полосу:
, то получим ослабление света, то есть темную полосу:
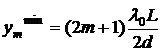 , где
, где  (13)
(13)
Минимум первого порядка при  :
:
 ,
,
то есть первый интерференционный минимум находится посередине между центральным и первым максимумом.
Расстояние между соседними светлыми или темными полосами:
 . (14)
. (14)
Из выражений (12) и (13) видно, что  зависит от длины волны
зависит от длины волны  . Если источники дают монохроматический свет (
. Если источники дают монохроматический свет ( ), то на экране получим чередующиеся темные и светлые полосы вполне определенного цвета, соответствующего данной длине волны.
), то на экране получим чередующиеся темные и светлые полосы вполне определенного цвета, соответствующего данной длине волны.
Если источники дают белый свет, то в луче присутствуют все длины волн видимого спектра, и будет различным для различных длин волн. Короткие длины волн, например, в максимуме первого порядка, дадут усиление ближе к центру; максимум более длинных волн будет находиться дальше от центра. Темных полос в случае белого света не будет, так как на минимум для одной длины волны накладывается максимум для другой длины волны. В центре экрана при  максимумы для всех длин волн совпадают и центральный максимум представляет собой яркую белую полосу. Соседние с ней светлые полосы будут радужными, обращенными фиолетовым краем к центральной белой полосе.
максимумы для всех длин волн совпадают и центральный максимум представляет собой яркую белую полосу. Соседние с ней светлые полосы будут радужными, обращенными фиолетовым краем к центральной белой полосе.
Описание установки
 На оптической скамье устанавливается осветитель О, светофильтр f, щель S, бипризма Б, линза С, зрительная труба с отчетной лупой Л (рис. 4).
На оптической скамье устанавливается осветитель О, светофильтр f, щель S, бипризма Б, линза С, зрительная труба с отчетной лупой Л (рис. 4).
Точная установка всех приборов обеспечивает четкую интерференционную картину. Для этого ребро бипризмы должно быть параллельно щели, щель должна быть узкой, середина щели и ребро бипризмы должны совпадать с оптической осью зрительной трубы.
Порядок выполнения работы
Из формулы(14) следует, что длина волны
 . (15)
. (15)
Для определения этой длины волны необходимо измерить расстояние между когерентными источниками света  , ширину интерференционной полосы
, ширину интерференционной полосы 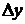 , расстояние
, расстояние 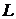 от когерентных источников до экрана, или до фокальной плоскости
от когерентных источников до экрана, или до фокальной плоскости  отсчетной лупы, где наблюдается интерференционная картина.
отсчетной лупы, где наблюдается интерференционная картина.
1. Включить осветитель. Щель и преломляющее ребро бипризмы установить вертикально и параллельно друг другу, то есть добиться того, чтобы свет от щели падал на ребро бипризмы.
2. Отрегулировать положение отсчетной лупы так, чтобы свет от щели падал на ее середину. Затем, перемещая бипризму вдоль оптической скамьи, добиться четкой интерференционной картины, которая представляет собой чередующиеся вертикальные темные и светлые полосы соответствующего фильтру цвета. После этого можно притупить к измерениям.
3. Определение расстояния  между мнимыми источниками.
между мнимыми источниками.
Между бипризмой и отсчетной лупой установить линзу (рис. 4 и 5) и перемещать ее вдоль скамьи, пока в отсчетной лупе не станут видны отчетливые изображения двух мнимых источников в виде двух ярких вертикальных изображений щели.

При этом положения щели, бипризмы и лупы не должны нарушаться. По шкале лупы измерить кажущееся расстояние  между источниками (рис. 5). Цена одного деления отсчетной лупы равна 0,1 мм.
между источниками (рис. 5). Цена одного деления отсчетной лупы равна 0,1 мм.
Затем определить истинное расстояние  между мнимыми источниками. Для этого измерить расстояние
между мнимыми источниками. Для этого измерить расстояние  от щели до линзы и расстояние
от щели до линзы и расстояние  от линзы до отсчетной лупы (до фокальной плоскости F). Из подобия заштрихованных треугольников на рис.5 получаем соотношение
от линзы до отсчетной лупы (до фокальной плоскости F). Из подобия заштрихованных треугольников на рис.5 получаем соотношение
 , откуда
, откуда  (16)
(16)
4. Определение ширины интерференционной полосы 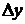 .
.
Снять с оптической скамьи линзу и по шкале лупы отсчитать число темных (или светлых) полос  , укладывающихся на некотором расстоянии шкалы. Затем подсчитать число делений шкалы
, укладывающихся на некотором расстоянии шкалы. Затем подсчитать число делений шкалы  на этом расстоянии.
на этом расстоянии.
Ширину интерференционной полосы определить по формуле:
 .
.
Эти измерения повторить не менее трех раз для разного числа интерференционных полос  и найти среднее значение
и найти среднее значение  .
.
5. По формуле (15) вычислить длину волны  , в которой
, в которой  - расстояние от щели до фокальной плоскости лупы.
- расстояние от щели до фокальной плоскости лупы.
Все измерения и вычисления проделать, используя красный и зеленый фильтры. Данные измерений и вычислений занести в таблицу.
Таблица измерений и вычислений
| Фильтр | № п/п | 
| 
| 
| 
| 
| 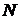
| 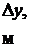
| 
| 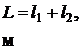
| 
| 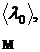
|
| Красный | 1. 2. 3. | |||||||||||
| Зелёный | 1. 2. 3. |
6. Сравнить полученные значения длин волн  для красного и зеленого света с указанными на светофильтрах или табличными данными.
для красного и зеленого света с указанными на светофильтрах или табличными данными.
Контрольные вопросы
1. Какова природа света?
2. Что называется интерференцией волн?
3. Какие волны являются когерентными?
4. Что называется оптическим ходом (оптической разностью хода) лучей?
5. Определить условия максимума и минимума интерференции волн.
6. Объяснить получение интерференционной картины с помощью бипризмы Френеля. Начертить ход лучей.
7. Вывести формулу, с помощью которой рассчитывается длина волны в данной работе.
8. Какие величины необходимо измерить в данной работе?
9. Как зависит ширина интерференционной полосы от длины волны?
10. Какой вид имеет интерференционная картина при освещении белым светом и почему?
Лабораторная работа № 4






