Заправочной системы.
Выше указывалось, что процесс заправки ЛА через централизованную заправочную систему представляет собой последовательное изменение числа подготавливаемых к заправке, находящихся одновременно под заправкой ЛА и аппаратов, на которых проводятся после заправочные операции, и что система обслуживания ЛА через ЦЗС может быть отнесена к системе массового обслуживания разомкнутого типа с неограниченным ожиданием.
Определение параметров, характеризующих процесс обслуживания ЛА в этом случае, осуществляется путем исследования п- канальной системы массового обслуживания, на вход которой поступает простейший поток заявок с интенсивностью X и интенсивностью обслуживания каждого канала \i: если поступившая заявка застанет свободным хотя бы один канал, она немедленно принимается за обслуживание и обслуживается до конца, в противном случае заявка попадает в очередь с количеством мест в очереди т. Очевидно, что т=0 получается система массового обслуживания с отказами, а при т ->оо - система с ожиданием. Каждая заявка может обслуживаться либо одним каналом - нет взаимопомощи между каналами - либо несколькими свободными каналами - есть взаимопомощь между каналами.
Для случая, когда отсутствует взаимопомощь между каналами обслуживания, состояние системы массового обслуживания разомкнутого типа описывается с помощью системы дифференциальных уравнений
Где Pk (t) -вероятность, что в момент времени t система будет находиться в состоянии Хк:Хк - в системе к заявок и они обслуживаются к каналами, очереди нет; Хш -в
системе имеется п+l заявок, причем и из них обслуживается и / заявок находится в очереди.
Интегрирование этой системы дифференциальных уравнений совместно с
нормировочным условием
позволяет найти все вероятные состояния системы массового обслуживания в произвольный момент времени в процессе выхода системы на стационарный режим, т.е. в процессе постановки ЛА на работу.
При стационарном режиме работы рассматриваемой системы массового обслуживания системы уравнений (1) превращается в систему алгебраических уравнений вида:
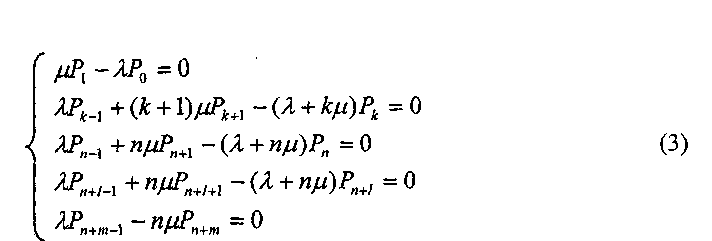
которая решается совместно с нормировочным условием (2) и дает следующие зависимости для определения вероятностей нахождения системы в состояниях Хк и Хп+1.
Зная вероятные состояния системы в любой момент времени, легко определить все параметры, характеризующие работу системы массового обслуживания.
Так, вероятность обслуживания определяется вероятностью того, что к моменту поступления ее на обслуживание, будет свободен хотя бы один канал или одно место в
очереди:
где Рп+т определяется по формуле (5).
Далее может быть определено среднее число занятых каналов:
где п -количество каналов обслуживания; f- среднее число заявок, поступавших в систему за среднее время обслуживания всеми каналами.
Вероятность того, что система полностью загружена, равна вероятности того, что в
системе заняты все каналы.
Среднее время неполной загрузки определяется из выражения
где t - среднее время полной загрузки системы.
Среднее число заявок, находящихся в очереди равно
Lср=ΣPn+l (11)
Среднее время ожидания заявок в очереди
t02=Lcp/ג
Среднее время нахождения заявки в системе складывается из средних времен
ожидания и обслуживания/
Таким образом, определены основные параметры, характеризующие качество работы централизованной системы заправки при отсутствии взаимопомощи между каналами обслуживания.
<
В том случае, когда существует взаимопомощь между каналами обслуживания, состояние системы массового обслуживания описывается с помощью системы дифференциальных уравнений вида:
состоянии которая превращается в систему алгебраических уравнений:
(15)
Параметры, характеризующие работу такой системы массового обслуживания, определяются выражениями аналогичными (6-13), в которых вероятности нахождения системы в состояниях Хк и Хп+1 находятся путем интегрирования системы
уравнений (14) совместно с нормировочным условием (12) для случая постановки ЛА на дежурство и путем решения системы уравнений (1) и (2) для стационарного режима работы централизованной заправочной системы с взаимопомощью между агрегатами обслуживания. В частности, для стационарного режима работы вероятность пребывания системы в /'-ом состоянии (j =0,1,2,3...,к,...,п,...,«+/,...п+т) находится из выражения/
Моделирование процесса функционирования системы заправки подвижными агрегатами обслуживания.
В том случае, когда заправка осуществляется подвижными агрегатами обслуживания, работа такой системы заправки может быть смоделирована замкнутой системой массового обслуживания, в которой число источников заявок ^ограничено количеством обслуживаемых ЛА, а интенсивность поступления заявок X зависит от состояний источников, обусловленных работой самой системы. Такая задача обычно решается в следующей постановке. Имеется N одинаковых взаимно удаленных объектов, каждый из которых может в некоторые случайные моменты времени подать заявку на обслуживание. ПотокзаявоккаждогообъектасчитаетсяПуассоновским с интенсивностьюX.Каждый объект может обслуживаться одним (нет взаимопомощи между каналами) или / из п (имеется частичная взаимопомощь) агрегатами обслуживания. Интенсивность пуассоновского потока обслуживание каждого канала р. Если к моменту подачи заявки объектом все каналы заняты, то этот объект становиться в очередь на обслуживание; дисциплина очереди такая: кто раньше подал заявку, тот раньше обслуживается.
Для случая отсутствия взаимопомощи между каналами обслуживания состояние замкнутой системы массового обслуживания описывается системой дифференциальных уравнений:
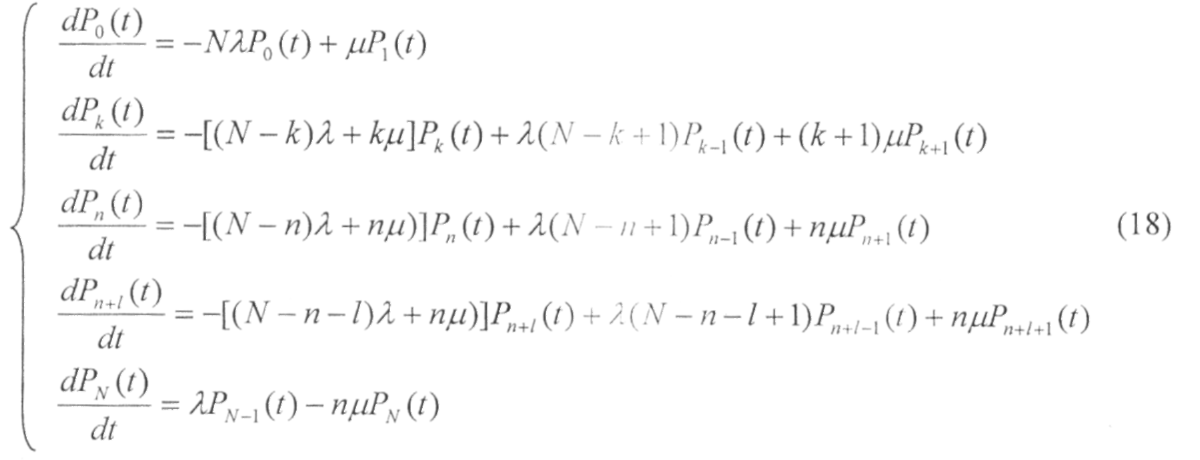
Решение системы дифференциальных уравнений (18) совместно с нормировочным условием 
позволяет определить все вероятные состояния замкнутой системы массового обслуживания и найти все параметры, характеризующие работу этой системы в режиме постановки ЛА на работу.
Для стационарного режима работы подвижных агрегатов обслуживания система (18) превращается в систему алгебраических уравнений:
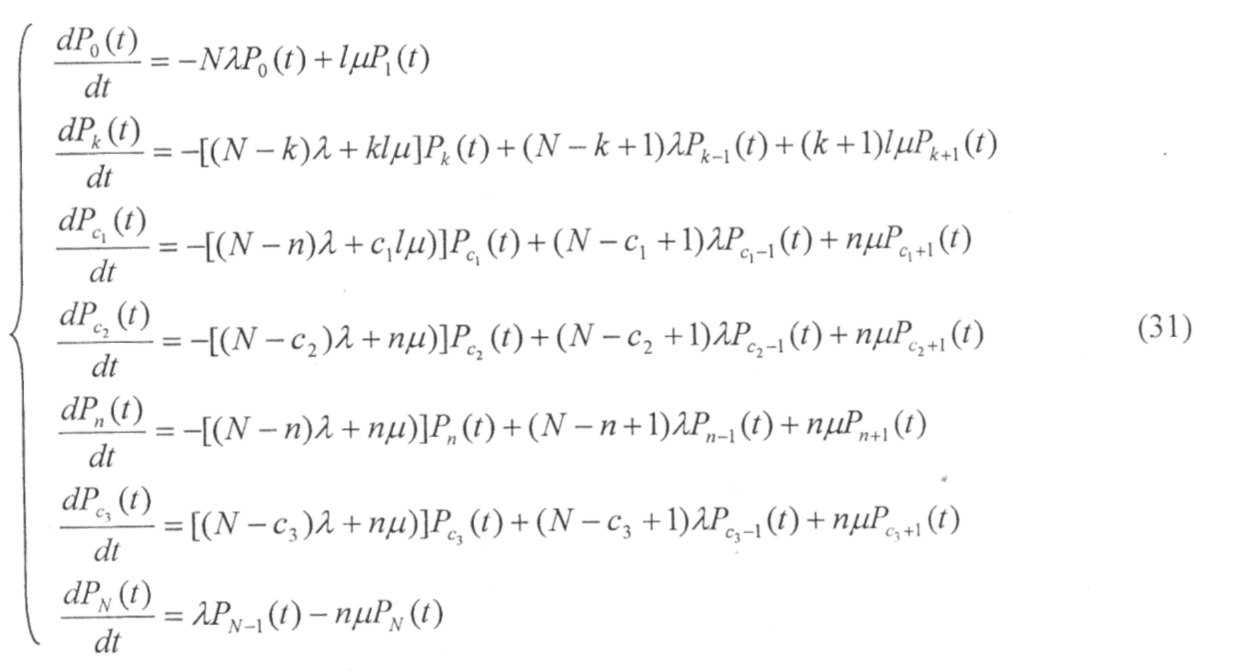
Эта система уравнений решается совместно с нормировочным условием (19) и дает возможность определить параметры, характеризующие работу заправочной системы с помощью подвижных агрегатов обслуживания в режиме постановки ЛА на работу.
Для стационарного режима работы такой системы массового обслуживания системы дифференциальных уравнений (31) преобразуются к виду:
В результате решения системы алгебраических уравнений (32), совместно с условием (19) получаются следующие выражения для определения вероятных состояний подобной системы массового обслуживания: 
Пример обслуживания подвижными агрегатами.
Имеется 30 взаимно удаленных объектов и три заправщика горючего. В среднем каждый объект нуждается в заправке (темп поступления заявки на обслуживание) 1 раз в 10 дней. Процесс заправки, включающий в себя время на передвижение, время на заправку самого агрегата и время на заправку объекта, длится в среднем одни сутки (темп выполнения заявки).
Определить:
а) вероятность того, что в данный момент времени объект не будет нуждаться в заправке;
б) среднее число объектов, нуждающихся в заправке;
в) среднее число объектов, ожидающих в заправки; 4
г) среднее время процесса заправки и ожидания;
д) среднее время ожидания в очереди.
Данный процесс заправки объектов представляет собой замкнутую систему обслуживания без взаимопомощи между агрегатами обслуживания: n =3 - количество каналов обслуживания;
N=30 - количество одинаковых взаимно удаленных объектов, являющихся источником заявок; 
Пользуясьформулами (23), определяем:
Вероятность того, что в данный момент объект не нуждается в заправке равна вероятности того, что заправочные агрегаты будут свободны (21), т.е. среднее число занятых (обслуживаемых объектов) агрегатов заправки определяется по формуле (24)
Р2 = 2,48
Среднее число объектов, ожидающих заправки (в очереди) находится из выражения (25)
P1 = 2,08
Среднее число простаивающих объектов (26)
Рпо =4,56
Вероятность того, что в данный момент времени объект не будет нуждаться в заправке, вычисляется по формуле (27)
Рис = 0,848
-это интенсивность использования, чем больше Рис, тем больше ЛА готовы к применению.
Среднее время процесса заправки и ожидания, т.е. простоя объекта (29)
tпр= 1,79 суток
Среднее время ожидания в очереди (30)
t02=0,79сут
Лабораторная работа №4
Определение оптимальнойстратегииобслуживания ЛА методом динамического программирования
Цель работы.
Цель работы заключается в ознакомлении студентов с методом динамического программирования и практическим его использованием при построении рациональной структуры наземного комплекса на примере выбора оптимального варианта заправочной системы.
Порядок проведения работ.
Изучить теоретическую часть лабораторной работы и ответить на контрольные вопросы.
Совместно с преподавателем выбрать вариант решаемой задачи. Варианты представлены в таблице №1.
Определить оптимальный вариант решения поставленной (выбранной) задачи методом динамического программирования.
Исходныеданные
Таблица №1
| Вариант Исходныевеличины | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Срок эксплуатации взаимно удаленных объектов, лет т | 4 | 6 | 3 | 5 | 5 | 9 | 6 | 7 | 6 | 3 | 6 | 8 | 9 | 5 | 2 | 3 | 4 | 8 | 4 | 8 |
| Количество доставляемого компонента топлива, Мо, единиц | 50 | 60 | 70 | 80 | 90 | 100 | 30 | 40 | 60 | 70 | 80 | 90 | 100 | 40 | 40 | 50 | 30 | 25 | 30 | 25 |
| Коэффициент в функции доставки первым способом, kз | 0,125 | 0,135 | 0,13 | 0,145 | 0,14 | 0,15 | 0,4 | 0,3 | 0,134 | 0,124 | 0,145 | 0,145 | 0,15 | 0,2 | 0,1 | 0,2 | 0,17 | 0,17 | 0,17 | 0,17 |
| Коэффициент в функции стоимости, k4 | 0,135 | 0,125 | 0,145 | 0,13 | 0,115 | 0,14 | 0,14 | 0,13 | 0,135 | 0,125 | 0,145 | 0,13 | 0,14 | 0,14 | 0,14 | 0,13 | 0,2 | 0,4 | 0,2 | 0,4 |
| Коэффициент в функции стоимости, k1 | 2 | 3 | 4 | 2 | 3 | 4 | 7 | 8 | 2 | 3 | 4 | 2 | 3 | 4 | 7 | 8 | 4 | 6 | 4 | 6 |
| Коэффициент в функции стоимости, k2 | 1 | 4 | 2 | 4 | 4 | 2 | 9 | 7 | 1 | 4 | 2 | 4 | 4 | 2 | 9 | 7 | 2 | 3 | 2 | 3 |
| Свободный член в функции стоимости, с1 | 75 | 80 | 85 | 70 | 80 | 85 | 55 | 60 | 75 | 80 | 85 | 70 | 80 | 85 | 55 | 60 | 65 | 60 | 65 | 60 |
| Свободный член в функции стоимости с2 | 80 | 75 | 70 | 85 | 85 | 80 | 75 | 80 | 80 | 75 | 70 | 85 | 85 | 80 | 75 | 80 | 75 | 85 | 75 | 85 |
| Показатель степени в функции стоимости n1 | 2 | 3 | 3 | 2 | 2 | 2 | 3 | 2 | 2 | 3 | 3 | 2 | 2 | 2 | 3 | 2 | 2 | 2 | 2 | 2 |
| Показатель степени в функции стоимости n2 | 5 | 2 | 3 | 3 | 2 | 2 | 1 | 2 | 5 | 2 | 3 | 3 | 2 | 2 | 1 | 5 | 3 | 4 | 3 | 4 |
3. Теоретическая часть.
3.1. Сущность метода динамического программирования.
Если показатель эффективности W складывается из нескольких слагаемых, получаемых на отдельных шагах, выигрыш за всю операцию равен сумме выигрышей на всех ее шагах. Такие операции называются многошаговыми, а метод оптимизации решений, наиболее приспособленный к задачам управления, такими операциями называется динамическим программированием.
Планируя многошаговую операцию, надо выбирать управление на каждом шаге с учетом последствий на предстоящих шагах. Этому правилу не подчиняется только последний шаг, который необходимо выбирать таким образом, чтобы он сам принес максимальную выгоду.
Поэтому процесс динамического программирования разворачивается от конца к началу: раньше планируется последний шаг, для ответа на вопрос чем окончился предпоследний, делают разные предположения. Для каждого из таких предположений находят условное оптимальное управление на последнем шаге и условный оптимальный выигрыш. После чего оптимизируется управление на предпоследнем шаге и так далее, пока не дойдем до первого шага.
После того, когда известны все условные оптимальные управления на всех шагах, мы знаем, как управлять процессом на любом очередном шаге, в каком бы состоянии ни был процесс к его началу. Теперь можно построить не условно-оптимальный, а просто оптимальное управление процессом, если повторить весь ход рассуждений с начала до конца.
Следовательно, в процессе поиска оптимального решения методом динамического программирования многошаговый процесс проходится дважды - от конца к началу и от начала к концу. Естественно, что первый этап значительно сложнее и длительнее второго. На втором только учитывается рекомендации первого этапа.
3.2. Определение стратегии обслуживания взаимно удаленных объектов
стационарными агрегатами обслуживания.
A. Постановка задачи.
Имеется определенное количество продукта (Мо), которое необходимо доставить к обслуживаемым объектам за т лет эксплуатации этих объектов. Доставка производится как с помощью общего стационарного агрегата, так и с помощью индивидуальных стационарных агрегатов. Полезная нагрузка, транспортируемая к объектам с помощью любого агрегата, требует ежегодных вложений (расходов), зависящих от того, сколько продукта какая система доставила. Если X продукта доставляется с помощью общего стационарного агрегата, то за год будет израсходовано f(X) средств: при этом не весь продукт может быть доставлен к концу года, так что к началу следующего года от него останется какая-то часть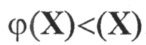 
. Аналогично, для доставки продукта Y с помощью
стационарных агрегатов индивидуального обслуживания, необходимо израсходовать (Y) средств, а к концу года останется от продукта какая-то часть 
. Поистечениигода,
оставшийся от Мо продукт заново распределяется между средствами доставки. Дополнительного продукта извне не поступает. Требуется найти такой способ обслуживания объектов (какие объекты какими агрегатами обслуживать в разные годы), при котором суммарные расходы будут минимальны.
B. Схема решения задачи.
Поставленную задачу целесообразно решать методом динамического программирования по следующей схеме.
Условным оптимальным управлением на i-ом шаге будем то из значений Xi, при котором выражение в фигурных скобках достигает минимума.
Д) Условный оптимальный выигрыш на последнем шаге будет
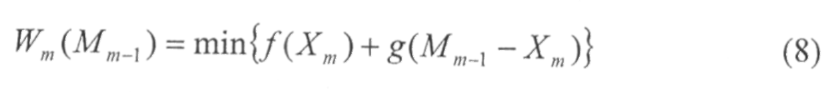
ему соответствует условное оптимальное управление Xm, при котором этот минимум достигается.
Е) Зная функцию Wm (Мm-1), находим по формуле основного функционального
управления (7) условные оптимальные затраты на двух последних, на трех последних и т.д. шагах:
……………………………………………
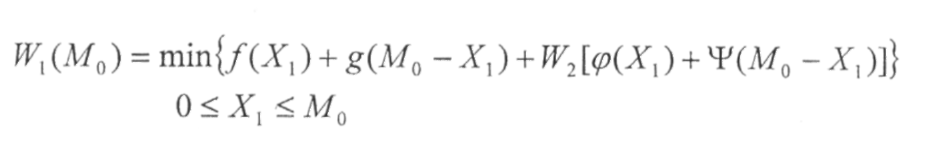
и соответствующие им условные оптимальные управления:
Ж) Начальное состояние MQ (начальный запас продукта) задано, поэтому минимальный расход (оптимальный выигрыш) будет 
Оптимальное управление на первом шаге будет
Состояниесистемыпослепервогошага
Оптимальноеуправлениенавторомшаге
и т.д. по цепочке. Состояние системы после / шагов описывается уравнением
Оптимальное управление на i-ом шаге
и т.д., вплоть до последнего шага, по цепочке
Величина Мm* представляет собой количество продукта, оставшегося (при оптимальном управлении) после последнего шага.
Совокупность продукта, доставляемого стационарным агрегатом общего пользования по годам 
будет представлять собой оптимальное управление, наряду с которым имеет место
- количество продукта, доставляемого стационарными агрегатами индивидуального пользования по годам.
3.3. Примеробслуживаниястационарнымиагрегатами
За 5 лет эксплуатации взаимно удаленных объектов требуется доставить М0 = 10 единиц определенного компонента топлива. Доставка осуществляется и с помощью общего агрегата, и с помощью индивидуальных стационарных агрегатов.
Выражения, связывающие между собой массу доставляемого компонента со стоимостью представим в виде:
Количество компонента, которое необходимо доставить к объектам за один год, известно, поэтому функции (Х) и (Y) могут быть заданы, например, в таком виде:
Требуется выбрать способ заправки компонента топлива взаимно удаленных объектов, исходя из минимума затрат. Решение поставленной задачи может быть выполнено методом динамического программирования следующим образом: Расход средств на /-ом шаге будет
Под влиянием этого управления X/ доставки компонента общим агрегатом система на /-ом шаге перейдет из состояния M;.j в состояние
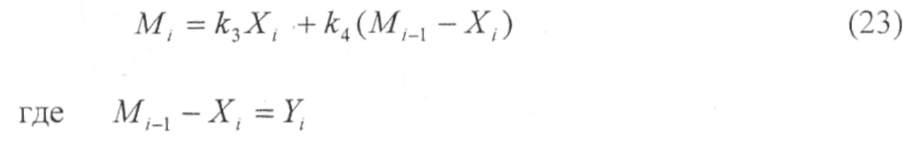
Основное функциональное управление имеет вид:
Условное оптимальное управление на i-ом шаге, при котором достигается этот минимум.
Условная оптимальная доставка компонента на последнем шаге (в последний год эксплуатации) будет определяться минимальным значением функции
Найдем этот минимум. Для этого возьмем первую производную и приравняем ее нулю, получим
Корни этого уравнения дают ответ на поставленный вопрос. Если задаться n1=n2=2,то будем иметь:
Следовательно, условное оптимальное управление на пятом шаге имеет вид
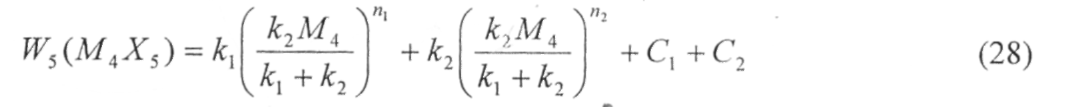
После этого, зная функцию W5 (М4Х5) находим в формуле основногофункционального управления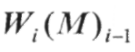 
оптимальные затраты на четвертом, третьем, втором и первом шагах, а также соответствующие этим условные оптимальным затратам условные управления.
Задание на лабораторную работу №5
Разработка технического плана и технологической схемы подготовки летательного аппарата к пуску.
Порядок выполнения работы:
1. Совместно с преподавателем выбрать ЛА, для обслуживания которого будет разрабатываться технологический план и технологическая схема подготовки его к пуску.
2. Определитьсостав и характеристики оборудования.
3. Выбрать проектные параметры транспортно-установочного агрегата.
4.Определить ветровые нагрузки, действующие на основные сооружения и системы наземного комплекса (при построении эпюры ветровой нагрузки для ракеты космического назначения, стоящей на стартовом сооружении вместе с башней обслуживания, представлять их равновесным цилиндром).
Задание на лабораторную работу №6
Разработка генплана пускового комплекса для летательного аппарата с учетом заданного азимута пуска.
Порядок выполнения работы:
1. Совместно с преподавателем выбрать ЛА, для обслуживания которого будет разрабатываться генеральный план пускового комплекса.
2. Обосновать состав сооружений и систем.
3. Определить между ними безопасные расстояния, с учетом допустимого давления ударной волны.
4.Определить расстояние до технического комплекса.
5. Выбрать проектные параметры башни обслуживания.
6.Оценить необходимое число обслуживающего персонала.
7.Оценить общую стоимость пускового комплекса и его основных частей.(Для группы студентов, которые не выполняли
ЛР№1)
Задание на лабораторную работу №7
Разработкапневмогидросхемы системы заправки ракеты космического назначения компонентами топлива.
Порядок выполнения работы:
1. Обосновать выбор элементов пневмо-гидравлической схемы и их количество.
2. Определить необходимые запасы компонентов в хранилищах и их потери при заправке.
3.Оценить временные характеристики технологического цикла подготовки. (Для группы студентов, которые не выполняли ЛР№1)
4.Разработать циклограмму процесса заправки;
5.Определить безопасные расстояния для размещения хранилищ компонентов топлива.
Задание на лабораторную работу №8
Разработка на уровне технических предложений систем наземного обеспечения для ракеты космического назначения.
Порядок выполнения работы:
1.Обосновать состав наземного комплекса и технические характеристики его частей.
2.Составить генпланы ТК и СК с учетом тротиловых эквивалентов компонентов топлива.
3.Определить нагрузки на элементы стартового комплекса от действия газовой струи, истекающей из сопла двигателя.
4.Выбрать проектные параметры монтажно-испытательного корпуса.
