На практике обычно объект находится либо с помощью РЛС, либо визуально.
В случае, когда центр рассеивания луча из – за флуктуаций объекта не совпадает с центром объекта и промах подчиняется нормальному закону распределения, вероятность нахождения с помощью РЛС определяетсяпоформуле
Отрезок от 
до (
Где – постоянная во всех направлениях дальность нахождения;
– смещение центра рассеивания или математического ожидание промаха;
– среднеквадратичное значение промаха;
– функция Лапласа
Если центр рассеивания совпадает с центром объекта, т.е. 
=0, то
Дальность нахождения с помощью РЛС определяется дальность прямой видимости
Где 
– высота антенны РЛС, м;
– высота полета объекта, м;
А – коэффициент характеризующий параметры локатора;
– эффективная поверхность рассеивания.
Вероятность захвата объекта.
Эффективность захвата объекта зависит от двух случайных событий – своевременного старта и от наличия зоны, образованной пересекающимися конусами вращения антенны РЛС и рассеиванием ЛА.
Вероятность захвата объекта определяется произведением двух величин: 
Где – вероятность попадания в зону захвата,
– вероятность своевременного запуска ЛА.
Вероятность попадания в зону захвата.
Вероятность попадания в зону захвата определяется при фиксированном угле пуска ЛА 
, а также при заданных угле полраствора антенны и расстоянии между РЛС и ПУ.
Если считать зону захвата кругом, то
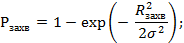
Где ϭ - среднеквадратичное значение ошибок наведения,
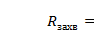– радиус зоны захвата,
– площадь зоны захвата,
– угол полу раствора антенны,
– угол наклона траектории при пуске,
d – расстояние между РЛС и ПУ.
Вероятность наведения на объект.
Нахождение объекта не всегда предполагает возможность действия.
Объект может находиться в таком положении относительно точки старта ЛА, что потребная перегрузка при наведении будет выше допустимой или присутствует факт лимита времени.
Если объект движется прямолинейно в горизонтальной плоскости, то вероятность наведения определяется вероятностью попадания в полосу, ограниченную справа и слева предельными значениями промаха, т.е.
Где 
– плотность распределения ошибок наведения;
– предельное отклонение, допускающее наведение.
Для нормального закона ошибок наведения этот интеграл распределяется через табличные функции Лапласа.
Где 
– среднеквадратическая ошибка наведения;
– математическое ожидание ошибки наведения (смещение центра рассеивания).
Лабораторная работа №3
Исследование процесса функционирования отдельных элементов
Наземного комплекса.
Цель работы.
Цель работы состоит в исследовании процесса функционирования технической и стартовой позиции, транспортного и заправочного оборудования путем представления их системами массового обслуживания различного вида.
