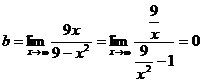
y = 0 – горизонтальная асимптота.
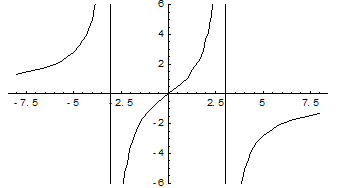
Пример. Найти асимптоты и построить график функции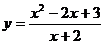 
.
Прямая х = -2 является вертикальной асимптотой кривой.
Найдем наклонные асимптоты.
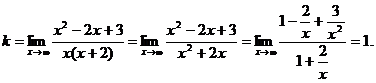
Итого, прямая у = х – 4 является наклонной асимптотой.
Схема исследования функций
Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать:
1) Область существования функции.
Это понятие включает в себя и область значений и область определения функции.
2) Точки разрыва. (Если они имеются).
3) Интервалы возрастания и убывания.
4) Точки максимума и минимума.
5) Максимальное и минимальное значение функции на ее области определения.
6) Области выпуклости и вогнутости.
7) Точки перегиба.(Если они имеются).
8) Асимптоты.(Если они имеются).
9) Построение графика.
Применение этой схемы рассмотрим на примере.
Пример. Исследовать функцию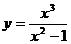 
и построить ее график.
Находим область существования функции. Очевидно, что областью определения функции является область (-¥; -1) È (-1; 1) È (1; ¥).
В свою очередь, видно, что прямые х = 1, х = -1 являются вертикальными асимптотами кривой.
Областью значений данной функции является интервал (-¥; ¥).
Точками разрыва функции являются точки х = 1, х = -1.
Находим критические точки.
Найдем производную функции
Критические точки: x = 0; x = -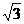 
; x = ; x = 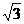-1; x = 1.
Найдем вторую производную функции
.
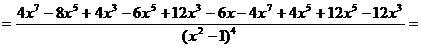
Определим выпуклость и вогнутость кривой на промежутках.
-¥ < x < - 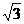, y¢¢ < 0, кривая выпуклая
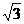- < x < -1, y¢¢ < 0, кривая выпуклая
-1 < x < 0, y¢¢ > 0, кривая вогнутая
0 < x < 1, y¢¢ < 0, кривая выпуклая
1 < x < 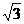, y¢¢ > 0, кривая вогнутая
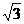< x < ¥, y¢¢ > 0, кривая вогнутая
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
-¥ < x < - 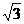, y¢ > 0, функция возрастает
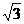- < x < -1, y¢ < 0, функция убывает
-1 < x < 0, y¢ < 0, функция убывает
0 < x < 1, y¢ < 0, функция убывает
1 < x < 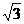, y¢ < 0, функция убывает
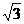< x < ¥, y¢¢ > 0, функция возрастает
Видно, что точка х = - 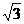является точкой максимума, а точка х = 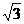является точкой минимума. Значения функции в этих точках равны соответственно -3 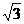/2 и 3 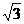/2.
Про вертикальные асимптоты было уже сказано выше. Теперь найдем наклонные асимптоты.
Итого, уравнение наклонной асимптоты – y = x.
Построим график функции:
Векторная функция скалярного аргумента.
z
A(x, y, z)
y
х
Пусть некоторая кривая в пространстве задана параметрически:
x = j(t); y = y(t); z = f(t);
Радиус- вектор произвольной точки кривой: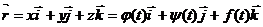 
.
Таким образом, радиус- вектор точки кривой может рассматриваться как некоторая векторная функция скалярного аргумента t. При изменении параметра t изменяется величина и направление вектора 
.
Запишем соотношения для некоторой точки t0:
Тогда вектор 
- предел функции (t). 
.
Очевидно, что
, тогда
.
Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.
 |
; 
;
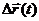
или, если существуют производные j¢(t), y¢(t), f¢(t), то
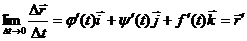
Это выражение – вектор производная вектора .
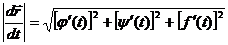
Если имеется уравнение кривой:
x = j(t); y = y(t); z = f(t);
то в произвольной точке кривой А(xА, yА, zА) с радиус- вектором
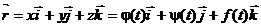
можно провести прямую с уравнением 
Т.к. производная - вектор, направленный по касательной к кривой, то
.
Свойства производной векторной функции скалярного аргумента.
1) 
2) 
, где l = l(t) – скалярная функция
3) 
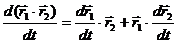
4) 
Уравнение нормальной плоскости к кривой будет иметь вид:
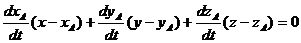
Пример. Составить уравнения касательной и нормальной плоскости к линии, заданной уравнением 
в точке t = p/2.
Уравнения, описывающие кривую, по осям координат имеют вид:
x(t) = cost; y(t) = sint; z(t) = 
;
Находим значения функций и их производных в заданной точке:
x ¢ (t) = -sint; y ¢ (t) = cost;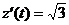 
x ¢ (p /2) = -1; y ¢ (p /2) = 0; z ¢ (p /2)=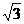
x(p /2) = 0; y(p /2) = 1; z(p /2)= p 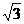/2
- это уравнение касательной.
Нормальная плоскость имеет уравнение:
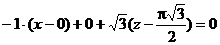
Параметрическое задание функции.
Исследование и построение графика кривой, которая задана системой уравнений вида:
,
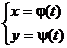производится в общем то аналогично исследованию функции вида y = f(x).
Находим производные:
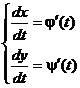
Теперь можно найти производную 
. Далее находятся значения параметра t, при которых хотя бы одна из производных j¢(t) или y¢(t) равна нулю или не существует. Такие значения параметра t называются критическими.
Для каждого интервала (t1, t2), (t2, t3), …, (tk-1, tk) находим соответствующий интервал (x1, x2), (x2, x3), …, (xk-1, xk) и определяем знак производной 
на каждом из полученных интервалов, тем самым определяя промежутки возрастания и убывания функции.
Далее находим вторую производную функции на каждом из интервалов и, определяя ее знак, находим направление выпуклости кривой в каждой точке.
Для нахождения асимптот находим такие значения t, при приближении к которым или х или у стремится к бесконечности, и такие значения t, при приближении к которым и х и у стремится к бесконечности.
В остальном исследование производится аналогичным также, как и исследование функции, заданной непосредственно.
На практике исследование параметрически заданных функций осуществляется, например, при нахождении траектории движущегося объекта, где роль параметра t выполняет время.
Ниже рассмотрим подробнее некоторые широко известные типы параметрически заданных кривых.
Уравнения некоторых типов кривых в параметрической
форме.
Окружность.
Если центр окружности находится в начале координат, то координаты любой ее
точки могут быть найдены по формулам:
0 £ t £ 3600
Если исключить параметр t, то получим каноническое уравнение окружности:
x2 + y2 = r2(cos2t + sin2t) = r2
Эллипс.
Каноническое уравнение: 
.
В
C M(x, y)
t
О N P
Для произвольной точки эллипса М(х, у) из геометрических соображений можно записать: 
из DОВР и 
из DOCN, где а- большая полуось эллипса, а b- меньшая полуось эллипса, х и у – координаты точки М.
Тогда получаем параметрические уравнения эллипса:
где 0 £ t £ 2p
Угол t называется эксцентрическим углом.
Циклоида.
у
С
М К
О Р В pа 2pа х
Определение. Циклоидой называется кривая, которую описывает некоторая точка, лежащая на окружности, когда окружность без скольжения катится по прямой.
Пусть окружность радиуса а перемещается без скольжения вдоль оси х. Тогда из геометрических соображений можно записать: OB = 
= at; PB = MK = asint;
ÐMCB = t; Тогда y = MP = KB = CB – CK = a – acost = a(1 – cost).
x = at – asint = a(t – sint).
Итого: 
при 0 £ t £ 2p - это параметрическое уравнение циклоиды.
Если исключить параметр, то получаем:
Как видно, параметрическое уравнение циклоиды намного удобнее в использовании, чем уравнение, непосредственно выражающее одну координату через другую.
Астроида.
Данная кривая представляет собой траекторию точки окружности радиуса a/4, вращающейся без скольжения по внутренней стороне окружности радиуса a.
 |
a/4
a
Параметрические уравнения, задающие изображенную выше кривую,
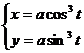, 0 £ t £ 2p,
Преобразуя, получим: x2/3 + y2/3 = a2/3(cos2t + sin2t) = a2/3
Производная функции, заданной параметрически.
Пусть 
Предположим, что эти функции имеют производные и функция x = j(t) имеет обратную функцию t = Ф(х).
Тогда функция у = y(t) может быть рассмотрена как сложная функция y = y[Ф(х)].
т.к. Ф(х) – обратная функция, то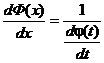 
Окончательно получаем: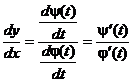 
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.
Пример. Найти производную функции
Способ 1: Выразим одну переменную через другую 
, тогда
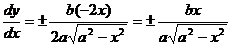
Способ 2: Применим параметрическое задание данной кривой: .
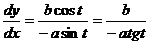
x2 = a2cos2t; 
Кривизна плоской кривой.
 |
a a
В
А А В
Определение: Угол a поворота касательной к кривой при переходе от точки А к точке В называется углом смежности.
Соответственно, более изогнута та кривая, у которой при одинаковой длине больше угол смежности.
Определение: Средней кривизной Кср дуги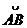 
называется отношение соответствующего угла смежности a к длине дуги .
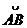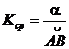
Отметим, что для одной кривой средняя кривизна ее различных частей может быть различной, т.е. данная величина характеризует не кривую целиком, а некоторый ее участок.
Определение: Кривизной дуги в точке КА называется предел средней кривизны при стремлении длины дуги 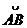® 0.
Легко видеть, что если обозначить 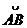= S, то при условии, что угол a - функция, которая зависит от S и дифференцируема, то
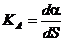
Определение: Радиусом кривизны кривой называется величина 
.
Пусть кривая задана уравнением y = f(x).
y
B
Dj
A j j+Dj
x
Kcp =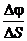 
; 
;
Если j = j(x) и S = S(x), то 
.
В то же время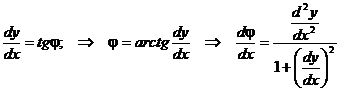 
.
Для дифференциала дуги: 
, тогда
Т.к.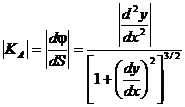 
. В других обозначениях: 
.
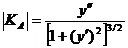Рассмотрим кривую, заданную уравнением: y = f(x).
 |
A
C(a, b)
Если построить в точке А кривой нормаль, направленную в сторону выпуклости, то можно отложить отрезок АС = R, где R – радиус кривизны кривой в точке А. Тогда точка С(a, b) называется центром кривизны кривой в точке А.
Круг радиуса R с центром в точке С называется кругом кривизны.
Очевидно, что в точке А кривизна кривой и кривизна окружности равны.
Можно показать, что координаты центра кривизны могут быть найдены по формулам:
Определение: Совокупность всех центров кривизны кривой линии образуют новую линию, которая называется эволютой по отношению к данной кривой. По отношению к эволюте исходная кривая называется эвольвентой.
Приведенные выше уравнения, определяющие координаты центров кривизны кривой определяют уравнение эволюты.
Свойства эволюты.
Теорема 1: Нормаль к данной кривой является касательной к ее эволюте.
Теорема 2: Модуль разности радиусов кривизны в любых точках кривой равен модулю длины соответствующей эволюты.
С3
С2 
С1 
R1 R2 R3
M1
M’1 M2 M3
M’2
M’3
Надо отметить, что какой – либо эволюте соответствует бесконечное число эвольвент.
Указанные выше свойства можно проиллюстрировать следующим образом: если на эволюту натянута нить, то эвольвента получается как траекторная линия конца нити при ее сматывании или разматывании при условии, что нить находится в натянутом состоянии.
Пример: Найти уравнение эволюты кривой, заданной уравнениями:
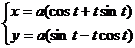
Уравнения эволюты: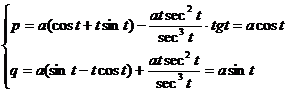 
Окончательно: 
- это уравнения окружности с центром в начале координат радиуса а. Исходная кривая получается своего рода разверткой окружности.
Ниже приведены графики исходной кривой и ее эволюты.
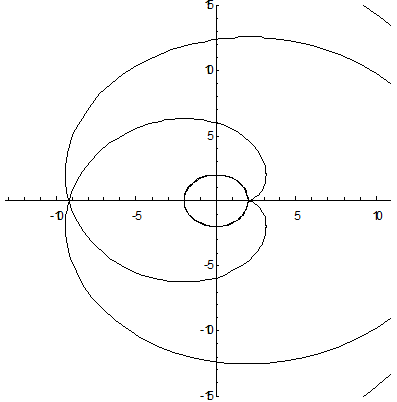
Кривизна пространственной кривой.
z
A(x, y, z)
B 
0 y
x
Для произвольной точки А, находящейся на пространственной кривой, координаты могут быть определены как функции некоторой длины дуги S.
x = j(S); y = y(S); z = f(S);
Приведенное выше уравнение называют векторным уравнением линии в пространстве.
Определение: Линия, которую опишет в пространстве переменный радиус – вектор 
при изменении параметра S, называется годографом этого вектора.
, тогда 
- вектор, направленный по касательной к кривой в точке А(x, y, z).
Но т.к. 
, то 
- единичный вектор, направленный по касательной.
Если принять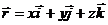 
, то 
.
Причем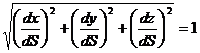 
.
Рассмотрим вторую производную 
Определение: Прямая, имеющая направление вектора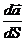 
называется главной нормалью к кривой. Ее единичный вектор обозначается 
.
