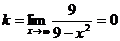В дальнейшем эта формула будет очень часто применяться для доказательства самых разных теорем.
Иногда формулу Лагранжа записывают в несколько другом виде:
 ,
,
где 0 < q < 1, Dx = b – a, Dy = f(b) – f(a).
Теорема Коши.
(Коши (1789-1857)- французский математик)
 Если функции f(x) и g(x) непрерывны на отрезке [ a, b] и дифференцируемы на интервале (a, b) и g ¢(x) ¹ 0 на интервале (a, b), то существует по крайней мере одна точка e, a < e < b, такая, что
Если функции f(x) и g(x) непрерывны на отрезке [ a, b] и дифференцируемы на интервале (a, b) и g ¢(x) ¹ 0 на интервале (a, b), то существует по крайней мере одна точка e, a < e < b, такая, что
 .
.
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке e.
Для доказательства этой теоремы на первый взгляд очень удобно воспользоваться теоремой Лагранжа. Записать формулу конечных разностей для каждой функции, а затем разделить их друг на друга. Однако, это представление ошибочно, т.к. точка e для каждой из функции в общем случае различна. Конечно, в некоторых частных случаях эта точка интервала может оказаться одинаковой для обеих функций, но это - очень редкое совпадение, а не правило, поэтому не может быть использовано для доказательства теоремы.
Доказательство. Рассмотрим вспомогательную функцию
 ,
,
которая на интервале [a, b] удовлетворяет условиям теоремы Ролля. Легко видеть, что при х = а и х = b F(a) = F(b) = 0. Тогда по теореме Ролля существует такая точка e,
a < e < b, такая, что F¢(e) = 0. Т.к.
 , то
, то

А т.к.  , то
, то 
Теорема доказана.
Следует отметить, что рассмотренная выше теорема Лагранжа является частным случаем (при g(x) = x) теоремы Коши. Доказанная нами теорема Коши очень широко используется для раскрытия так называемых неопределенностей. Применение полученных результатов позволяет существенно упростить процесс вычисления пределов функций, что будет подробно рассмотрено ниже.
Раскрытие неопределенностей.
Правило Лопиталя.
(Лопиталь (1661-1704) – французский математик)
К разряду неопределенностей принято относить следующие соотношения:

Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g ¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х ®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.

Доказательство. Применив формулу Коши, получим:

где e - точка, находящаяся между а и х. Учитывая, что f(a) = g(a) = 0:

Пусть при х®а отношение  стремится к некоторому пределу. Т.к. точка e лежит между точками а и х, то при х®а получим e®а, а следовательно и отношение
стремится к некоторому пределу. Т.к. точка e лежит между точками а и х, то при х®а получим e®а, а следовательно и отношение  стремится к тому же пределу. Таким образом, можно записать:
стремится к тому же пределу. Таким образом, можно записать:
 .
.
Теорема доказана.
Пример: Найти предел  .
.
Как видно, при попытке непосредственного вычисления предела получается неопределенность вида  . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
f¢(x) = 2x +  ; g¢(x) = ex;
; g¢(x) = ex;
 ;
;
Пример: Найти предел 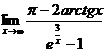 .
.
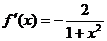 ;
;  ;
;
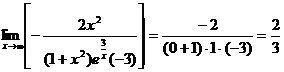 .
.
Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
Пример: Найти предел  .
.
 ;
;  ;
;
 ;
;  ;
;

 ;
;  ;
; 
Следует отметить, что правило Лопиталя – всего лишь один из способов вычисления пределов. Часто в конкретном примере наряду с правилом Лопиталя может быть использован и какой – либо другой метод (замена переменных, домножение и др.).
Пример: Найти предел  .
.
 ;
;  ;
;
 - опять получилась неопределенность. Применим правило Лопиталя еще раз.
- опять получилась неопределенность. Применим правило Лопиталя еще раз.
 ;
;  ;
;
 - применяем правило Лопиталя еще раз.
- применяем правило Лопиталя еще раз.
 ;
; 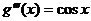 ;
;
 ;
;
Неопределенности вида  можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида
можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида  , f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).
, f(x)>0 вблизи точки а при х®а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).
Пример: Найти предел  .
.
Здесь y = xx, lny = xlnx.
Тогда  . Следовательно
. Следовательно 
Пример: Найти предел  .
.
 ;
;  - получили неопределенность. Применяем правило Лопиталя еще раз.
- получили неопределенность. Применяем правило Лопиталя еще раз.
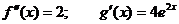 ;
;  ;
;
Производные и дифференциалы высших порядков.
Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную

Если найти производную функции f¢(x), получим вторую производную функции f(x).

т.е. y¢¢ = (y¢)¢ или  .
.
Этот процесс можно продолжить и далее, находя производные степени n.
 .
.
Общие правила нахождения высших производных.
Если функции u = f(x) и v = g(x) дифференцируемы, то
1) (Сu)(n) = Cu(n);
2) (u ± v)(n) = u(n) ± v(n);
3) 
 .
.
Это выражение называется формулой Лейбница.
Также по формуле dny = f(n)(x)dxn может быть найден дифференциал n- го порядка.
Исследование функций с помощью производной.
Возрастание и убывание функций.
Теорема. 1) Если функция f(x) имеет производную на отрезке [ a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f ¢(x) ³ 0.
2) Если функция f(x) непрерывна на отрезке [ a, b] и дифференцируема на промежутке (а, b), причем f ¢(x) > 0 для a < x < b, то эта функция возрастает на отрезке [ a, b].
Доказательство.
1) Если функция f(x) возрастает, то f(x + Dx) > f(x) при Dx>0 и f(x + Dx) < f(x) при Dх<0,
тогда:

2) Пусть f¢(x)>0 для любых точек х1 и х2, принадлежащих отрезку [a, b], причем x1<x2.
Тогда по теореме Лагранжа: f(x2) – f(x1) = f¢(e)(x2 – x1), x1 < e < x2
По условию f¢(e)>0, следовательно, f(x2) – f(x1) >0, т.е. функция f(x) возрастает.
Теорема доказана.
Аналогично можно сделать вывод о том, что если функция f(x) убывает на отрезке [a, b], то f¢(x)£0 на этом отрезке. Если f¢(x)<0 в промежутке (a, b), то f(x) убывает на отрезке [a, b].
Конечно, данное утверждение справедливо, если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b).
 Доказанную выше теорему можно проиллюстрировать геометрически:
Доказанную выше теорему можно проиллюстрировать геометрически:
y y
j j j j
x x
Точки экстремума.
Определение. Функция f(x) имеет в точке х1 максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х1. Функция f(x) имеет в точке х2 минимум, если f(x2 +Dx) > f(x2) при любом Dх (Dх может быть и отрицательным).
Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.
Определение. Точки максимума и минимума функции называются точками экстремума.
Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х1 и точка х1 является точкой экстремума, то производная функции обращается в нуль в этой точке.
Доказательство. Предположим, что функция f(x) имеет в точке х = х1 максимум.
Тогда при достаточно малых положительных Dх>0 верно неравенство:
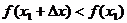 , т.е.
, т.е.

Тогда


По определению:
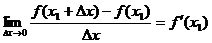
Т.е. если Dх®0, но Dх<0, то f¢(x1) ³ 0, а если Dх®0, но Dх>0, то f¢(x1) £ 0.
А возможно это только в том случае, если при Dх®0 f¢(x1) = 0.
Для случая, если функция f(x) имеет в точке х2 минимум теорема доказывается аналогично.
Теорема доказана.
Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.
Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.
Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.
Пример: f(x) = ôxô Пример: f(x) = 
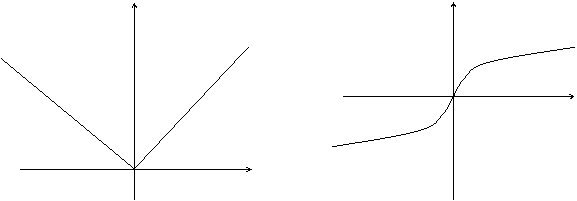 y y
y y
x
x
В точке х = 0 функция имеет минимум, но В точке х = 0 функция не имеет ни
не имеет производной. максимума, ни минимума, ни произ-
водной.
Вообще говоря, функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю.
Теорема. (Достаточные условия существования экстремума)
Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х1).
Если при переходе через точку х1 слева направо производная функции f ¢(x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.
Доказательство.
Пусть 
По теореме Лагранжа: f(x) – f(x1) = f ¢(e)(x – x1), где x < e < x1.
Тогда: 1) Если х < x1, то e < x1; f¢(e)>0; f¢(e)(x – x1)<0, следовательно
f(x) – f(x1)<0 или f(x) < f(x1).
2) Если х > x1, то e > x1 f¢(e)<0; f¢(e)(x – x1)<0, следовательно
f(x) – f(x1)<0 или f(x) < f(x1).
Т. к. ответы совпадают, то можно сказать, что f(x) < f(x1) в любых точках вблизи х1, т.е. х1 – точка максимума.
Доказательство теоремы для точки минимума производится аналогично.
Теорема доказана.
На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:
1) Найти критические точки функции.
2) Найти значения функции в критических точках.
3) Найти значения функции на концах отрезка.
4) Выбрать среди полученных значений наибольшее и наименьшее.
Исследование функции на экстремум с помощью
производных высших порядков.
Пусть в точке х = х1 f¢(x1) = 0 и f¢¢(x1) существует и непрерывна в некоторой окрестности точки х1.
Теорема. Если f ¢(x1) = 0, то функция f(x) в точке х = х1 имеет максимум, если f ¢¢(x1)<0 и минимум, если f ¢¢(x1)>0.
Доказательство.
Пусть f¢(x1) = 0 и f¢¢(x1)<0. Т.к. функция f(x) непрерывна, то f¢¢(x1) будет отрицательной и в некоторой малой окрестности точки х1.
Т.к. f¢¢(x) = (f¢(x))¢ < 0, то f¢(x) убывает на отрезке, содержащем точку х1, но f¢(x1)=0, т.е. f¢(x) > 0 при х<x1 и f¢(x) < 0 при x>x1. Это и означает, что при переходе через точку х = х1 производная f¢(x) меняет знак с “+” на “-“, т.е. в этой точке функция f(x) имеет максимум.
Для случая минимума функции теорема доказывается аналогично.
Если f¢¢(x) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.
Выпуклость и вогнутость кривой.
Точки перегиба.
Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.
 у
у
x
На рисунке показана иллюстрация приведенного выше определения.
Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).
Доказательство. Пусть х0 Î (a, b). Проведем касательную к кривой в этой точке.
Уравнение кривой: y = f(x);
Уравнение касательной: 
Следует доказать, что  .
.
По теореме Лагранжа для f(x) – f(x0):  , x0 < c < x.
, x0 < c < x.

По теореме Лагранжа для 

Пусть х > x0 тогда x0 < c1 < c < x. Т.к. x – x0 > 0 и c – x0 > 0, и кроме того по условию
 , следовательно,
, следовательно,  .
.
Пусть x < x0 тогда x < c < c1 < x0 и x – x0 < 0, c – x0 < 0, т.к. по условию  то
то
 .
.
Аналогично доказывается, что если f¢¢(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).
Теорема доказана.
Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная пересекает кривую.
Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f ¢¢(a) = 0 или f ¢¢(a) не существует и при переходе через точку х = а f ¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
Доказательство. 1) Пусть f¢¢(x) < 0 при х < a и f¢¢(x) > 0 при x > a. Тогда при
x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба.
2) Пусть f¢¢(x) > 0 при x < b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.
Теорема доказана.
Асимптоты.
При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.
Определение. Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.
Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.
Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике функции  . Ее наклонная асимптота у = х.
. Ее наклонная асимптота у = х.

Рассмотрим подробнее методы нахождения асимптот кривых.
Вертикальные асимптоты.
Из определения асимптоты следует, что если  или
или  или
или  , то прямая х = а – асимптота кривой y = f(x).
, то прямая х = а – асимптота кривой y = f(x).
Например, для функции  прямая х = 5 является вертикальной асимптотой.
прямая х = 5 является вертикальной асимптотой.
Наклонные асимптоты.
Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b.




 M
M
 |
j
N
j P
Q
Обозначим точку пересечения кривой и перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью Ох обозначим j. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N.
Тогда MQ = y – ордината точки кривой, NQ =  - ордината точки N на асимптоте.
- ордината точки N на асимптоте.
По условию:  , ÐNMP = j,
, ÐNMP = j,  .
.
Угол j - постоянный и не равный 900, тогда
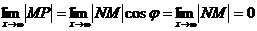

Тогда  .
.
Итак, прямая y = kx + b – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.
В полученном выражении выносим за скобки х:

Т.к. х®¥, то  , т.к. b = const, то
, т.к. b = const, то  .
.
Тогда  , следовательно,
, следовательно,

 .
.
Т.к.  , то
, то  , следовательно,
, следовательно,

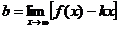
Отметим, что горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0.
Пример. Найти асимптоты и построить график функции  .
.
1) Вертикальные асимптоты: y®+¥ x®0-0: y®-¥ x®0+0, следовательно, х = 0- вертикальная асимптота.
2) Наклонные асимптоты:


Таким образом, прямая у = х + 2 является наклонной асимптотой.
Построим график функции:

Пример. Найти асимптоты и построить график функции  .
.
Прямые х = 3 и х = -3 являются вертикальными асимптотами кривой.
Найдем наклонные асимптоты: