Второй основной задачей статики является определение условий, при которых заданная система сил эквивалентна нулю (уравновешена).
Теорема.
Система сил эквивалентна нулю (уравновешена) тогда и только тогда, когда её главный вектор и главный момент относительно произвольной точки равны нулю.
Доказательство. Приведём заданную систему сил к произвольно выбранному центру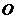 
. В соответствии с теоремой о приведении системы сил к одному центру, исходная система сил эквивалентна одной силе 
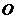, приложенной в выбранном центре , и одной паре сил 
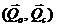, момент которой 
, т.е.
причём 
Силы 
и 
заменим равнодействующей 
(Рис. 2.2). Таким образом, любую систему сил можно заменить эквивалентной системой двух сил. При этом
(a)
(b)
Аксиома 2 устанавливает необходимые и достаточные условия равновесия системы двух сил, приложенных к абсолютно твёрдому телу – силы должны быть равными по модулю, противоположными по направлению 
и, кроме того, должны иметь общую линию действия (Рис. 2.3), т.е. 
| 
| |
| Рис. 2.2 | Рис. 2.3 | |
Сравнивая последние равенства с равенствами (a) и (b), находим, что для равновесия произвольной системы сил необходимо и достаточно, чтобы геометрическая сумма всех сил системы (главный вектор) равнялась нулю и сумма моментов всех сил системы относительно произвольно выбранной точки (главный момент) равнялась нулю:
Принимая центр приведения за начало декартовой системы координат, получаем в проекциях на координатные оси:
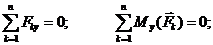
Таким образом,
для равновесия произвольной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трёх взаимно перпендикулярных осей координат равнялась нулю и сумма моментов всех сил системы относительно каждой из этих осей равнялась нулю.
Эквивалентность систем сил
Теорема.
Две системы сил, приложенные к свободному твёрдому телу, эквивалентны тогда и только тогда, когда их главные векторы и главные моменты относительно одного и того же произвольно выбранного центра равны между собой.
Доказательство. Пусть две системы сил эквивалентны: 
Покажем, что главные векторы и главные моменты этих систем сил равны между собой. Используя принцип независимости действия сил, выберем вспомогательную систему сил 
такую, что 
и, следовательно, 
. При этом действие заданных систем сил на тело (в составе новых систем сил) не изменяется. Условия равновесия для расширенных систем сил имеют вид:
Сравнивая равенства и , получаем:
или 
Таким образом, доказана необходимость условий для эквивалентности систем сил.
Докажем достаточность. Пусть условия выполнены. Покажем, что системы сил при этом эквивалентны. Рассмотрим вспомогательную систему сил , для которой справедливы равенства , и, следовательно, справедливы равенства . На основании теоремы об условиях равновесия системы сил отсюда получаем
.
На основании аксиомы 2 к любой системе сил можно добавить или от неё отнять уравновешенную систему сил. Отсюда:
Теорема Вариньона
Из теоремы об эквивалентности вытекает очень важное следствие, которое в литературе обычно формулируют как теорему Вариньона:
если система сил имеет равнодействующую, то момент равнодействующей относительно произвольно выбранной точки равен сумме моментов всех сил системы относительно этой точки.
