В соответствии с теоремой об эквивалентности систем сил, две пары сил эквивалентны тогда и только тогда, когда равны их моменты. Отсюда следует, что, не изменяя действия пары сил на абсолютно твёрдое тело, можно производить следующие преобразования пар сил (Рис. 2.4 – 2.6):
1. переносить и поворачивать пару сил в плоскости её действия;
2. переносить пару сил в любую плоскость, параллельную плоскости
действия пары сил;
3. изменять плечо и модули сил, образующих пару, так чтобы модуль
момента пары оставался неизменным.
| 
| 
| ||
| Рис. 2.4 | Рис. 2.5 | Рис. 2.6 | ||
Доказанная ранее теорема о сложении пар оказывается справедливой при произвольном расположении пар сил в пространстве, поскольку в случае параллельности плоскостей действия, пары сил можно перенести в одну плоскость.
|
| Рис. 2.7 |
Таким образом,
Две произвольно расположенные пары сил эквивалентны одной паре сил, момент которой равен сумме моментов слагаемых пар сил.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
- Сформулировать необходимые и достаточные условия равновесия системы сил.
- Сформулировать необходимые и достаточные условия эквивалентности систем сил.
- Сформулировать необходимые и достаточные условия эквивалентности пар сил.
- Как можно видоизменять пару сил, не изменяя её действие на абсолютно твёрдое тело?
- Сформулировать теорему Вариньона.
ЛЕКЦИЯ 4
3. ОБЪЁМНЫЕ И ПОВЕРХНОСТНЫЕ СИЛЫ
До сих пор мы оперировали так называемыми сосредоточенными силами, которые имеют определённую точку приложения (или линию действия). Сосредоточенная сила является одной из абстракций, используемых в механике. Реальные взаимодействия материальных тел всегда представляются распределёнными либо по объёму тела, либо по его поверхности. К поверхностным силам относятся силы давления, т.е. силы контактного действия, а к объёмным – гравитационные и электромагнитные силы. Сосредоточенные силы появляются в теории как равнодействующие поверхностных или объёмных сил.
Центр параллельных сил
При изучении объёмных и поверхностных сил широко используется центр параллельных сил. Это понятие вводится для системы параллельных сил, имеющих равнодействующую, причём точки приложения сил системы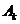 
считаются фиксированными.
Центром параллельных сил называется точка, вокруг которой поворачивается равнодействующая системы параллельных сил при повороте всех сил системы вокруг своих точек приложения в одну и ту же сторону на один и тот же угол.
|
| Рис.3.1 |
Найдём положение центра параллельных сил 
для системы 
, имеющей равнодействующую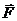 
. Пусть 
– единичный вектор, параллельный линиям действия сил системы (Рис. 3.1). Тогда 
, где 
– проекция силы на направление единичного вектора 
. Для равнодействующей получаем:
Для любого центра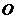 
, используя теорему Вариньона, получаем:
или 
Вынося за скобку общий множитель 
получаем:
или 
где 
Векторное произведение равно нулю, если один из сомножителей равен нулю или если сомножители коллинеарны. Но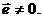 
Повернём все силы системы вокруг своих точек приложения в одну и ту же сторону на один и тот же угол (Рис. 3.1). Равнодействующая системы сил повернётся вокруг точки C в ту же сторону на тот же угол. Вместе с силами поворачивается вокруг точки O и вектор . В результате этой операции вектор изменил направление; вектор 
остался неизменным, но по-прежнему 
Следовательно, 
т.е.
Отсюда
(1)
Примем точку O за начало декартовой системы координат. Записывая формулу (1) в проекциях на координатные оси, получаем координаты центра параллельных сил:
Центр тяжести
Центром тяжести называется точка тела, через которую проходит линия действия его силы тяжести при любом положении тела по отношению к Земле.
Экспериментально такую точку можно найти последовательно подвешивая тело на нити за различные точки. При равновесии тело находится под действием двух сил – силы тяжести и реакции нити, которые по аксиоме 2 должны располагать по одной прямой – вдоль нити, т.е. по местной вертикали.
Рассмотрим материальное тело, расположенное вблизи поверхности Земли (в поле силы тяжести). Допустим сначала, что тело состоит из конечного числа материальных точек, другими словами, частиц, размерами которых можно пренебречь. На каждую частицу с номером 
действует сила тяжести 
. Если размеры тела малы по сравнению с размерами Земли, то систему сил тяжести частиц можно рассматривать как систему параллельных сил, направленных в одну сторону. Такая система сил всегда имеет равнодействующую 
, модуль которой часто называют весом тела. При любом изменении ориентации тела по отношению к Земле силы тяжести частиц остаются вертикальными, т.е. они поворачиваются по отношению к телу вокруг своих точек приложения. Линия действия силы тяжести тела при этом всегда будет проходить через определённую точку – центр параллельных сил, который в рассматриваемом случае называется центром тяжести тела. Таким образом, положение центра тяжести тела, состоящего из конечного числа частиц, можно определить по формуле (1):
(2)
При определении положения центра тяжести сплошного тела это тело разбивается сечениями, параллельными координатным плоскостям, на элементарные объёмы (Рис. 3.2) и центр тяжести тела определяется как предел последовательности радиусов-векторов центров тяжести системы элементарных объёмов (частиц) при объёме каждой частицы, стремящемся к нулю:
,
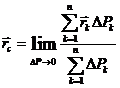где 
- радиус-вектор элементарного объёма; 
- вес частицы.
Этот предел представляет собой, по определению, интеграл
При вычислении подобных интегралов переходят к интегрированию по объёму, для чего вводится понятие удельного веса
,
где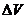 
– элемент объёма.
|
| Рис. 4.2 |
Таким образом,
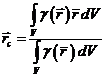(3)
Формула (3) является наиболее общей для определения положения центра тяжести сплошного тела.
Если удельный вес тела не зависит от координат, тело называется однородным. Для однородных тел, полагая в формуле (3) 
, получаем:
, (4)
где 
– объём тела.
Если однородное тело представляет собой пластину постоянной толщины 
, то 
, 
, где 
– площадь поверхности пластины. В этом случае для определения положения центра тяжести тела необходимо вычислить поверхностный интеграл:
(5)
Если однородное тело представляет собой стержень с постоянной площадью поперечного сечения 
, то 
, 
и формула (4.4) принимает вид:
, (6)
где 
– длина стержня.
Во многих случаях положение центра тяжести тела можно определить при помощи весьма простых методов. Рассмотрим некоторые из них.
Симметрия однородных тел. Если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости. Для доказательства этого утверждения примем плоскость симметрии за координатную плоскость 
. Записывая формулу (4) в проекциях на координатную ось 
, получаем:
поскольку область интегрирования разбивается на две симметричные области 
и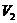 
, в первой из которых 
, а во второй 
.
Аналогично можно показать, что если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси; если однородное тело имеет центр симметрии, то центр тяжести тела совпадает с его центром симметрии.
Метод разбиений состоит в том, что тело разбивается на конечное число частей, положение центров тяжести которых известно. Положение центра тяжести тела определяется по формуле (2).
Пример 3.1.
Определить положение центра тяжести однородной пластины,
изображённой на Рис. 3.3.
|
| Рис. 3.3 |
Разобьём пластину на два прямоугольника с площадям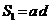и 
и 
Прямоугольники обладают осевой симметрией и их центры тяжести находятся в точке пересечения диагоналей
и 
Для однородной пластины постоянной толщины вес пропорционален площади поверхности. В проекциях на координатные оси из формулы (2) получаем:
.
Метод дополнений или метод отрицательных масс представляет собой частный случай метода разбиений, применяется для тел имеющих вырезы (полости), вес которых (для однородных тел – объём или площадь) считается отрицательным.
Пример 3.2.
Определить положение центра тяжести однородной пластины, изображённой на Рис. 3.4.
Прежде всего заметим, что пластина имеет ось симметрии, проходящую через центр пластины и центр выреза. Примем эту ось за координатную ось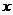 
. Тогда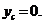 
Разобьём пластину на две части: круг без выреза радиуса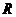 
и вырез радиуса 
с центром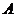 
. При этом 
Используя формулу (2), получаем:
|
| |
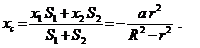
| Рис. 3.4 | Рис. 3/5 |
Пример 3.3.
Определить положение центра тяжести однородной треугольной пластины, изображённой на Рис. 3.5.
Разобьём треугольник на элементарные полоски, параллельные одной из сторон, например, стороне 
. Центр тяжести каждой полоски в силу симметрии лежит на её середине, а центр тяжести треугольники расположен, следовательно, на медиане 
. Проводя аналогичное разбиение параллельно другой стороне, например 
, получаем, что центр тяжести лежит на медиане 
. Таким образом, центр тяжести однородного треугольника расположен в точке пересечения его медиан.
Пример 3.4.
Определить положение центра тяжести однородной дуги
окружности радиуса 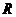с центральным углом 
(Рис. 3.6).
Начало координат совместим с центром окружности, ось 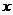направим перпендикулярно хорде , стягивающей дугу. В этом случае ось 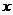будет осью симметрии тела и, следовательно, 
. Для вычисления 
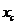используем формулу (6):
причём, 
Тогда
| 
| |
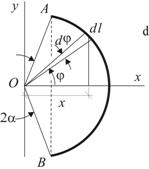
| Рис. 3.6 | Рис. 3.7 |
Пример 3.5.
Определить положение центра тяжести однородного кругового сектора радиуса 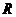с центральным углом 
(Рис. 3.7).
Разобьём пластину на элементарные круговые секторы. Каждый элементарный сектор можно рассматривать как равнобедренный треугольник, центр тяжести которого расположен в точке пересечения медиан, которые, как известно, делятся точкой пересечения в отношении 2:1. Таким образом, центр тяжести рассматриваемого кругового сектора совпадает с центром тяжести однородной дуги окружности радиуса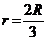 
и таким же центральным углом. Используя результат, полученный в предыдущем примере, находим:
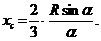
Положение центра тяжести играет важную роль в вопросах устойчивости и предотвращения опрокидывания сооружений.
В заключение заметим, что при определении положения центра тяжести как вид результата, так и трудоёмкость его получения существенно зависят от выбора системы координат.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
- Что называется центром параллельных сил?
- По каким формулам определяются координаты центра параллельных сил?
- Что называется центром тяжести тела?
- В чём состоит метод разбиений для вычисления координат центра тяжести тела?
- В чём состоит метод отрицательных масс для вычисления координат центра тяжести тела?
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплект СР-14.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
