Одной из основных задач статики является приведение системы сил к простейшему виду, т.е. преобразование заданной системы сил в другую, ей эквивалентную, но содержащую минимальное число сил. Одним из способов решения такой задачи является приведение системы сил к одному центру (метод Пуансо).
Теорема.
Произвольная система сил эквивалентна системе, состоящей из одной силы, равной геометрической сумме всех сил системы, приложенной в произвольно выбранной точке (центре приведения), и одной пары сил, момент которой равен сумме моментов всех сил системы относительно этой точки.
|
| Рис. 2.1 |
Доказательство. Пусть задана система сил 
, произвольным образом расположенных в пространстве (Рис. 2.1). Выберем любую точку 
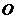в качестве центра приведения. Рассмотрим любую силу системы 
. На основании аксиомы 2 приложим к точке 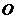уравновешенную систему сил 
, причём, 
. Таким образом, сила оказывается эквивалентной системе трёх сил, состоящей из такой же по модулю и направлению силы 
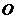, приложенной в точке , и пары сил 
, момент которой равен моменту силы относительно точки .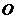
Проделывая такую операцию с каждой силой системы, заменяем заданную систему сил эквивалентной, которая состоит из приложенных в точке 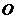сил 
и пар сил 
, плоскости действия которых имеют общую точку .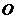
В соответствии с аксиомой 1 система сил эквивалентна одной силе 
, приложенной в точке 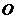и равной геометрической сумме всех заданных сил:
.
В соответствии с теоремой о сложении пар система пар сил эквивалентна одной паре, момент которой равен сумме моментов слагаемых пар, т.е. сумме моментов всех сил исходной системы относительно точки :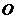
.
Таким образом, установлены две важнейшие характеристики системы сил:
главным вектором системы сил называется геометрическая сумма всех сил системы:
главным моментом системы сил относительно некоторого центра O называется геометрическая сумма моментов всех сил системы относительно точки O:
Вектор главного момента изображают приложенным в той точке , относительно которой он вычисляется.
Заметим, что главный вектор и главный момент системы сил представляют собой чисто геометрические величины и не могут рассматриваться как некоторая сила или момент некоторой силы.
Доказанную выше теорему о приведении системы сил к одному центру теперь можно сформулировать в виде:
Произвольная система сил эквивалентна системе, состоящей из одной силы, равной главному вектору системы сил, приложенной в произвольно выбранной точке (центре приведения), и одной пары сил, момент которой равен главному моменту системы сил относительно этой точки.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
- Что называется парой сил?
- Что называется моментом пары сил?
- Как располагается вектор момента пары сил по отношению к паре сил?
- Чем можно заменить систему пар, плоскости действия которых пересекаются в одной точке?
- Чем заменяется любая система сил после её приведения к одному центру?
- Что называется главным вектором системы сил?
- Что общего и в чём различие между главным вектором и равнодействующей системы сил?
- Что называется главным моментом системы сил относительно центра?
ЛЕКЦИЯ 3
