Задача 4. Найти производные 
, пользуясь правилами и формулами дифференцирования.
1) a) y = (5 x 4 – 
+3)2, 8) y = 
,
2) а) y = (4 x 3 + 
-2)5, 9) y = 
,
3) а) y = (7 x 5–3 
- 5)4, 10) y = 
,
4) а) y = (3 x 4 + 
-3)5, 11) y= 
,
5) а) y = (6 x 3 –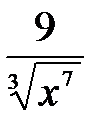 
+ 6)5, 12) y = 
,
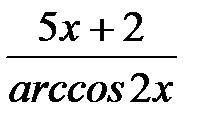6) а) y = (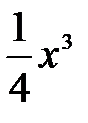
–5 
+2)3, 13) y = 
,
7) а) y =(2 x 2–3 
–1)3, 14) y =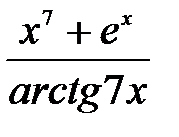 
,
Задача 5. Вычислить определенный интеграл (Табл. 2.1).
Таблица 2.1
| Вариант | Функция | Вариант | Функция |
| 1 | 
| 8 | 
|
| 2 | 
| 9 |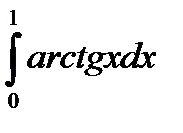 
|
| 3 | 
| 10 | 
|
| 4 |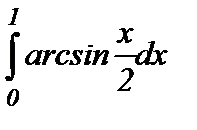 
| 11 |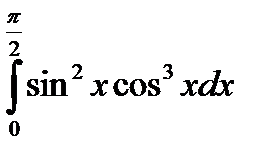 
|
| 5 |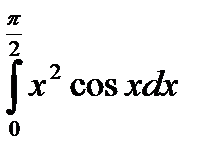 
| 12 | 
|
| 6 | 
| 13 | 
|
| 7 | 
| 14 |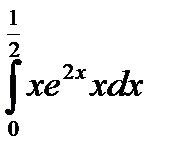 
|
Задача 6.
Тест 1. Заданы множества А={2,3,4,5} и D={3,4,5}. Верным для них будет утверждение:
Варианты ответов:
1) множество А - подмножество множества D;
2) множество D - подмножество множества A;
3) множество А и множество D равны.
Тест 2. Если отношение задано неравенством: 3x-4y<0, то данному отношению принадлежит следующая пара чисел?
Варианты ответов:
1) (0;1); 2) (3;1); 3) (2;0); 4) (3, 2).
Тест 3. На факультете учатся студенты, имеющие домашний персональный компьютер и студенты, не имеющие домашнего персонального компьютера. Пусть А - множество всех студентов факультета; В - множество студентов факультета, имеющих домашний персональный компьютер. Тогда разностью А\В этих множеств будет
Варианты ответов:
1) множество студентов факультета, не имеющих домашнего персонального компьютера;
2) множество студентов факультета, имеющих домашний персональный компьютер;
3) все множество студентов факультета.
Тест 4. Если А - множество четных натуральных чисел, а В={11, 22, 33, 44, 55, 66, 77}, то количество элементов множества АÇВ равно
Варианты ответов:
1) 7; 2) 3; 3) 5; 4) 10.
Тест 5. Пусть множество M=(-1;1) представляет собой интервал, а множество N=[-1;0) - отрезок числовой оси, тогда множество K=M ÈN, как числовой промежуток будет равно
Варианты ответов:
1) K=[-1, 1]; 2) K=(-1,0]; 3) K=(-1,0); 4) K=(-1, 1).
Перечень основной и дополнительной учебной литературы, необходимой для освоения дисциплины (модуля)
а) Основная литература:
1. Высшая математика для экономистов / под ред. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2013. – 479 с. (ЭБС Айбукс. www.ibooks.ru)
2. Огнева Э. Н., сост. Математические методы исследования. Кемерово: КемГУКИ, 2012 г., 43 с. (ЭБС Айбукс. www.ibooks.ru).
б) Дополнительная литература:
3. Теория вероятностей и математическая статистика / под ред. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2012. – 551 с. (ЭБС Айбукс. www.ibooks.ru)
4. Сборник задач по высшей математике для экономистов / под ред. В.И. Ермакова. – М.: ИНФРА-М, 2009. – 575 с.
Перечень ресурсов информационно-телекоммуникационной сети «Интернет», необходимых для освоения дисциплины (модуля)
а) электронные образовательные ресурсы (ЭОР):
- www.edu.ru - Российское образование. Федеральный образовательный портал;
- http://mgei.ru/dopolnitelno/razdel_2/lichnyj_kabinet_eios/ - электронная образовательная среда (ЭОС) МГЭУ
- http://www.webmath.ru/ - образовательный математический портал.
б) электронно-библиотечные системы (ЭБС):
| № п/п | Дисциплина | Ссылка на информационный ресурс | Наименование разработки в электронной форме | Доступность/срок действия договора |
| 1. | «Математика и статистика» | http://www.biblioclub.ru | Электронно-библиотечная система (ЭБС) Университетская библиотека онлайн | Индивидуальный неограниченный доступ из любой точки, в которой имеется доступ к сети Интернет/ 05.07.2017 г.-09.07.2018 г. |
| 2. | «Математика и статистика» | www.ibooks.ru | Электронно-библиотечная система (ЭБС) | Индивидуальный неограниченный доступ из любой точки, в которой имеется доступ к сети Интернет/ 15.04.2017 г.-14.04.2018 г. |
