Контрольная работапо дисциплине
«МАТЕМАТИКА И СТАТИСТИКА»
Направление подготовки 38.03.02Менеджмент
Направленность (профиль) основной профессиональной образовательной программы прикладногобакалавриата: «Управление человеческими ресурсами»
| Формы обучения: | очная, заочная |
| Виды профессиональной деятельности: | организационно-управленческая |
Тверь 2018
Пояснения
Контрольная работа содержит два теоретических вопроса и шесть задач. Варианты вопросов и задач выбираются по номеру журнала учебной группы. Работа оформляется в печатном виде (задачи могут быть решены в отдельной тетради). Объем теоретической части – не менее 10 стр. стандартного печатного текста. Если номер превышает значение 14, например – 15, то выбирается значение 1.
Первый вопрос
1. Понятие матрицы. Виды матриц. Операции над матрицами. Свойства операций над матрицами.
2. Определители квадратных матриц. Формулы для вычисления определителей матриц первого и второго порядка.
3. Правило Сарруса вычисления определителей матриц третьего порядка. Минор и алгебраическое дополнение элемента квадратной матрицы.
4. Теорема Лапласа и схема ее применения для вычисления определителей квадратных матриц любого порядка.
5. Свойства определителей.
6. Обратная матрица. Необходимое и достаточное условие существования обратной матрицы.Алгоритм вычисления обратной матрицы.
7. Ранг матрицы. Теорема о неизменности ранга матрицы при ее элементарных преобразованиях.Теорема о ранге матрицы.
8. Системы линейных уравнений и формы их математического представления.
9. Определитель системы.Теорема Крамера.
10. Метод Гаусса решения систем линейных уравнений.Теорема Кронекера-Копелли.
11. Совместная, несовместная, неопределенная и определенная системы линейных уравнений.
12. Векторы на плоскости и в пространстве.Скалярное произведение векторов.
13. Векторное пространство, его размерность и базис.
14. Линейная зависимость векторов. Линейное пространство.Зависимость координат вектора в разных базисах.
15. Евклидово пространство.Норма вектора. Ортонормированный базис.
16. Линейные операторы и операции над ними.Собственные векторы и собственные значения линейного оператора.
17. Характеристический многочлен линейного оператора.
18. Квадратичная форма. Приведение квадратичной формы к каноническому виду.
19. Понятие множества. Операции над множествами. Числовые множества.
20. Модуль действительного числа. Окрестность точки.
21. Определение функции. Способы задания функции. Свойства функций. Обратная функция. Сложная функция. Элементарные функции. Классификация функций.
22. Преобразование графиков функций.
23. Числовая последовательность. Предел числовой последовательности. Геометрический смысл предела числовой последовательности.
24. Предел функции в бесконечности и его геометрический смысл. Предел функции в точке и его геометрический смысл.
25. Бесконечно малые величины и их связь с пределами функций. Свойства бесконечно малых величин.
26. Бесконечно большие величины. Их свойства.
27. Основные теоремы о пределах.
28. Признаки существования предела. Замечательные пределы. Способы вычисления пределов функций.
29. Непрерывность функции в точке. Точки разрыва функции и их классификация.
30. Свойства функций, непрерывных в точке. Свойства функций, непрерывных на отрезке.Теорема Вейерштрасса.Теорема Больцано-Коши.
Второй вопрос
1. Определение производной функции. Геометрический и механический смысл производной. Зависимость между непрерывностью функции и дифференцируемостью. Схема вычисления производной.
2. Основные правила дифференцирования. Производная сложной и обратной функции. Производные основных элементарных функций.
3. Предел и непрерывность функции двух переменных. Частные производные и дифференциал функции двух переменных.Производная по направлению и градиент.
4. Экстремумы функции нескольких переменных. Необходимое и достаточное условия экстремума функции двух переменных.
5. Первообразная функции и неопределенный интеграл. Свойства неопределенного интеграла.Интегралы от основных элементарных функций. Методы нахождения неопределенных интегралов.
6. Интегрирование иррациональных и тригонометрических функций. Функции, не интегрируемые в конечном виде.
7. Определенный интеграл, его геометрический смысл. Достаточное условие интегрируемости функций.Свойства определенного интеграла. Теорема о среднем.
8. Формула Ньютона-Лейбница. Замена переменной и формула интегрирования по частям в определенном интеграле.
9. Геометрические приложения определенного интеграла. Вычисление площади плоской фигуры. Вычисление объемов тел вращения.
10. Приближенное вычисление определенных интегралов.
11. Дифференциальные уравнения первого порядка. Теорема существования и единственности его решения.
12. Дифференциальные уравнения с разделяющимися переменными.
13. Однородные дифференциальные уравнения первого порядка.
14. Использование дифференциальных уравнений в экономической динамике. Модель естественного роста. Модель роста в условиях конкурентного рынка.
15. Классическое определение вероятности событий. Свойства вероятности событий.
16. Основные формулы комбинаторики.Статистическая вероятность. Геометрическая вероятность.
17. Теорема сложения вероятностей.Полная группа событий. Противоположные события.Теорема умножения вероятностей.
18. Формула полной вероятности. Формула Байеса. Формула Бернулли.
19. Дискретные и непрерывные случайные величины. Закон распределения дискретной случайной величины.
20. Биномиальное распределение. Распределение Пуассона. Простейший поток событий.
21. Числовые характеристики дискретных случайных величин, их свойства.Закон больших чисел.
22. Теорема Чебышева.Теорема Бернулли.
23. Закон равномерного распределения вероятности.Нормальный закон распределения.
24. Правило трех сигм. Мода, медиана, асимметрия и эксцесс распределения. Показательное распределение.
25. Генеральная и выборочная совокупности. Виды выборок.
26. Эмпирическая функция распределения. Полигон и гистограмма.
27. Статистические оценки параметров распределения. Выборочная дисперсия, несмещенная выборочная дисперсия.
28. Доверительные интервалы для оценки математического ожидания нормального распределения и среднего квадратического отклонения.
29. Статистическая гипотеза. Ошибки первого и второго рода. Область принятия гипотезы. Критические точки. Мощность критерия.
30. Сравнение дисперсий двух генеральных совокупностей.
Раздел I. Основы линейной алгебры и математического анализа
Задача 1. Вычислить предел функции (табл.1.1).
Таблица 1.1
| Вариант | Предел | Вариант | Предел |
| 1 | 
| 8 | 
|
| 2 | 
| 9 | 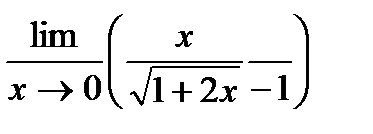
|
| 3 | 
| 10 | 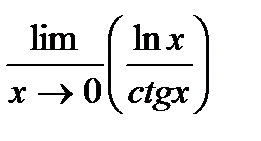
|
| 4 | 
| 11 | 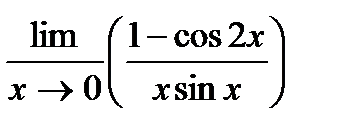
|
| 5 | 
| 12 | 
|
| 6 | 
| 13 | 
|
| 7 | 
| 14 | 
|
Задача 2. Исследовать функцию (табл. 1.2) и построить ее график.
Таблица 1.2
| Вариант | Функция | Вариант | Функция |
| 1 | 
| 8 | 
|
| 2 | 
| 9 | 
|
| 3 | 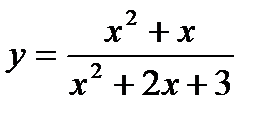
| 10 | 
|
| 4 | 
| 11 | 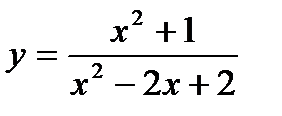
|
| 5 | 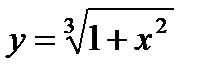
| 12 | 
|
| 6 | 
| 13 | 
|
| 7 | 
| 14 | 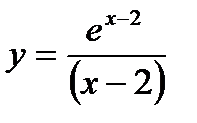
|
Задача 3. Найти решение следующей системы линейных уравнений (табл. 1.3) методом Гаусса:
a11x1 +а12х2 +а13х3 = b1
а21x1 +a22x2 +a23x3 = b2
a31x1 +а32x2 +а33хз = b3
Таблица 1.3
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 5 |
| a11 | 1 | 2 | 3 | 4 | 5 | 6 | 5 |
| a12 | 8 | 6 | 4 | 3 | 2 | 3 | 4 |
| a13 | 5 | 3 | 6 | 3 | 4 | 3 | 6 |
| a 21 | 4 | 6 | 8 | 3 | 2 | 4 | 3 |
| a 22 | 3 | 4 | 3 | 2 | 3 | 6 | 3 |
| a 23 | 5 | 4 | 3 | 2 | 1 | 2 | 3 |
| а31 | 5 | 4 | 3 | 2 | 1 | 2 | 3 |
| а 32 | 1 | 2 | 4 | 6 | 8 | 3 | 5 |
| а 33 | 3 | 4 | 3 | 2 | 3 | 6 | 3 |
| b1 | 5 | 4 | 3 | 2 | 1 | 2 | 3 |
| b2 | 3 | 4 | 3 | 2 | 3 | 6 | 3 |
| b3 | 1 | 2 | 4 | 6 | 8 | 3 | 5 |
| Вариант | 8 | 9 | 10 | 11 | 12 | 13 | 1 4 |
| a11 | 1 | 2 | 3 | 4 | 5 | 6 | 5 |
| a12 | 5 | 4 | 3 | 2 | 1 | 2 | 3 |
| a13 | 4 | 6 | 8 | 3 | 2 | 4 | 3 |
| a 21 | 1 | 2 | 4 | 6 | 8 | 3 | 5 |
| a 22 | 5 | 4 | 3 | 2 | 1 | 2 | 3 |
| a 23 | 1 | 2 | 4 | 6 | 8 | 3 | 5 |
| а31 | 3 | 1 | 3 | 2 | 3 | 6 | 3 |
| а 32 | 5 | 4 | 3 | 2 | 1 | 2 | 3 |
| а 33 | 1 | 2 | 3 | 4 | 5 | 6 | 5 |
| b1 | 6 | 6 | 4 | 3 | 2 | 3 | 4 |
| b2 | 3 | 4 | 3 | 2 | 3 | 6 | 3 |
| b3 | 4 | 6 | 8 | 3 | 2 | 4 | 3 |




