Лекция 11
Тема:Функции комплексного переменного. Предел, непрерывность, производная. Аналитическая функция. Условие Коши-Римана.
11.1.Комплексные числа в алгебраической и тригонометрической форме и действия над ними.
Число z=x+ i y, где х и у действительные числа, а 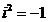 или
или  , называется комплексным числом в алгебраической форме.
, называется комплексным числом в алгебраической форме.
Число  называется действительной частью комплексного числа, а
называется действительной частью комплексного числа, а  - мнимой частью. Комплексное число изображается точкой на комплексной плоскости.
- мнимой частью. Комплексное число изображается точкой на комплексной плоскости.

Модуль комплексного числа есть расстояние от точки z до начала координат и обозначается |z|,  . Сопряженным числом для z=x+iy называется число
. Сопряженным числом для z=x+iy называется число 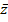 =x-iy.
=x-iy.  .
.
Действия над комплексными числами в алгебраической форме.
1) Сложение комплексных чисел.

2) Умножение комплексных чисел.
Умножение комплексных чисел производится по правилу умножения многочлена на многочлен, учитывая, что 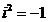 .
.

3) Деление комплексных чисел.

Тригонометрическая форма комплексного числа.
Пусть z=x+iy.

Рассмотрим полярную систему координат с полюсом в т. О и полярой ОХ. В этом случае формулы перехода от декартовой системы координат к полярной имеют вид:
 ,
,
и комплексное число z запишется в виде z= 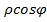 + i
+ i  =
= 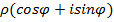 ,
,
 z =| z |(cos
z =| z |(cos  + isin
+ isin  ) – Это и есть тригонометрическая форма комплексного числа,
) – Это и есть тригонометрическая форма комплексного числа,  .
.
Модуль комплексного числа, определяется однозначно:  а Argz определен лишь с точностью до любого слагаемого, кратного 2π. Через argz обозначается главное значение Argz, которое является одним из значений Argz.
а Argz определен лишь с точностью до любого слагаемого, кратного 2π. Через argz обозначается главное значение Argz, которое является одним из значений Argz.
Умножение комплексных чисел в тригонометрической форме.

В частности,  .
.
Функции комплексного переменного.
Определение 1: Говорят, что на множестве Е точек комплексной плоскости z задана функция w=f(z), если по вполне определенному закону каждой точке  ставится в соответствие точка w или совокупность точек. В первом случае функция называется однозначной, а во втором случае многозначной.
ставится в соответствие точка w или совокупность точек. В первом случае функция называется однозначной, а во втором случае многозначной.
Множество Е называется множеством определения функции f(z), а множество Q всех значений w, которые принимает f(z) на Е, - множеством ее изменений. Наиболее важным случаем является тот, когда Е и Q являются областями.
Если положить z=x+iy, a w=U(x,y)+i  (x,y), то задание функции комплексного переменного w=f(z) равносильно заданию двух функций двух переменных U(x,y) и
(x,y), то задание функции комплексного переменного w=f(z) равносильно заданию двух функций двух переменных U(x,y) и  (x,y). Функция U(x,y) называется действительной частью, а
(x,y). Функция U(x,y) называется действительной частью, а  (x,y) – мнимой частью функции w=f(z).
(x,y) – мнимой частью функции w=f(z).
Предел, непрерывность, производная функции комплексного переменного.
Пусть функция w=f(z) определена и однозначна в некоторой окрестности точки  , кроме, быть может самой точки
, кроме, быть может самой точки  .
.
Будем говорить, что предел функции w=f(z) существует при  , если существуют оба предела
, если существуют оба предела  , при этом будем полагать:
, при этом будем полагать:  .
.
Так как определение предела функции f(z) сводится к определению предела действительных функций, то теоремы о пределе суммы, произведения, частного сохраняются и для функций комплексного переменного.
Определение 2: Определение предела функции комплексного переменного можно сформулировать и с помощью понятия окрестности.
Число  называется пределом функции W=f(z) в точке
называется пределом функции W=f(z) в точке  , если
, если  , то
, то  . Отметим, что f(z) стремится к
. Отметим, что f(z) стремится к  независимо от способа приближения точки z к
независимо от способа приближения точки z к  . Таким образом, если
. Таким образом, если 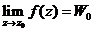 , то при стремлении z к
, то при стремлении z к  по какой-либо линии, f(z) будет стремиться к
по какой-либо линии, f(z) будет стремиться к  .
.
Определение 3: Пусть функция W=f(z) определена в некоторой окрестности точки  (включая саму точку
(включая саму точку  ). Функция W=f(z) называется непрерывной в точке
). Функция W=f(z) называется непрерывной в точке  , если предел функции в точке
, если предел функции в точке  равен значению функции в этой точке, т.е.
равен значению функции в этой точке, т.е.  .
.
Отметим, для того, чтобы функция f(z)=U(x,y)+  (x,y) была непрерывной в точке
(x,y) была непрерывной в точке  необходимо и достаточно, чтобы обе функции U(x,y) и
необходимо и достаточно, чтобы обе функции U(x,y) и  (x,y) были непрерывны в точке
(x,y) были непрерывны в точке  .
.
Так как определение непрерывности функции комплексного переменного аналогично определению непрерывности функции действительного переменного, то теоремы о непрерывности суммы, произведения, частного остаются справедливыми и для функций комплексного переменного.
Определение 4: Пусть f(z) определена в некоторой окрестности точки z, включая саму точку z. Производной функции f(z) в точке z называется предел:

В этом случае говорят, что функция f(z) дифференцируема в точке z.
Условия дифференцируемости функции f(z)=U(x,y)+  (x,y) в терминах действительных функций U(x,y) и
(x,y) в терминах действительных функций U(x,y) и  (x,y) выражаются в следующей теореме:
(x,y) выражаются в следующей теореме:
Теорема. (Условия Коши-Римана)(Эйлера-Даламбера).
Пусть f(z)=U(x,y)+  (x,y) определена в некоторой окрестности точки z, причем U(x,y) и
(x,y) определена в некоторой окрестности точки z, причем U(x,y) и  (x,y) непрерывны в точке z вместе со своими частными производными первого порядка. Для того, чтобы f(z) имела в точке z производную (f(z) была дифференцируема в точке z) необходимо и достаточно выполнение условий:
(x,y) непрерывны в точке z вместе со своими частными производными первого порядка. Для того, чтобы f(z) имела в точке z производную (f(z) была дифференцируема в точке z) необходимо и достаточно выполнение условий:
 (условия Коши-Римана).
(условия Коши-Римана).
Доказательство.
Необходимость. Дано: f(z) в точке z имеет производную. Требуется доказать, что выполняются равенства  . Так как
. Так как  существует, то
существует, то  , где
, где 
Пусть  , тогда
, тогда 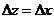 .
.

Далее, положим, что  =0, тогда
=0, тогда 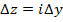 . Отсюда следует равенство
. Отсюда следует равенство
 =
= 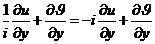
 . Так как два комплексных числа равны, то равны соответственно их действительные и мнимые части,
. Так как два комплексных числа равны, то равны соответственно их действительные и мнимые части,  и
и 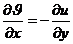 . Это означает, что выполняются условия Коши-Римана.
. Это означает, что выполняются условия Коши-Римана.
Достаточность.
Дано  ,
, 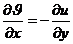 . Требуется доказать, что
. Требуется доказать, что  существует.
существует.
Так как U(x,y) и  (x,y) имеют непрерывные частные производные в точке (х,у), то они дифференцируемы в этой точке. Это означает, что
(x,y) имеют непрерывные частные производные в точке (х,у), то они дифференцируемы в этой точке. Это означает, что
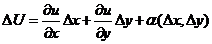 , где
, где 

 +
+  , где
, где  .
.
Далее имеем:
 , где
, где 
Учитывая условия Коши-Римана, будем иметь:


Так как обычные свойства алгебраических действий и предельного перехода сохраняются при переходе к функциям комплексного переменного, то сохраняются обычные правила дифференцирования.

 , где u=g(z);
, где u=g(z); 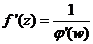 , где f(z) и
, где f(z) и  взаимно обратные функции.
взаимно обратные функции.
C учетом условий Коши-Римана, производную f’(z) можно находить по формуле:  .
.
Определение 5. Функция называется аналитической в области, если она имеет производную в каждой точке этой области.
Отметим, что понятие аналитической функции относится только к однозначным функциям, т.к. понятие предела и производной было дано для однозначных функций.
Пример 1. Проверить выполнение условий Коши-Римана для функции  и найти ее производную.
и найти ее производную.
Решение. 
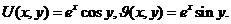

Следовательно,  , кроме этого отметим, что U(x,y) и
, кроме этого отметим, что U(x,y) и  (x,y) непрерывны вместе со своими частными производными первого порядка на всей плоскости. Таким образом, условия Коши-Римана выполняются. Производную найдем по формуле:
(x,y) непрерывны вместе со своими частными производными первого порядка на всей плоскости. Таким образом, условия Коши-Римана выполняются. Производную найдем по формуле:
 .
. 






