Мнимые и комплексные числа были введены в математику, в известном смысле, против воли математиков (отсюда и термин – мнимые). Дело в том, что они оказались совершенно необходимы при решении кубических уравнений.
Основным элементом, отличающим комплексные числа от действительных, является мнимая единица. Мнимой единицей называется квадратный корень из минус единицы. Она обозначается либо с помощью буквы i, либо с помощью знака квадратного корня – 
. Таким образом, основное свойство мнимой единицы таково: i2 = –1.
Комплексные числа являются результатом умножения мнимой единицы на действительные числа и сложения результата с теми же действительными числами. Каждое комплексное число с имеет вид a + bi. Действительное число а называется действительной частью комплексного числа с. Действительное число b называется мнимой частью комплексного числа с. Число a – bi называется комплексно сопряжённым с исходным числом a + bi.
На комплексные числа переносятся обычные математические операции. Пусть с1 = a1 + b1i, а с2 = a2 + b2i, тогда:
1. Формула с1 + с2 = (a1 + a2) + (b1 + b2)i определяет сложение. Вычитание определяется аналогично.
2. Формула с1 ∙ с2 = (a1a2 – b1b2) + (a1b2 + a2b1)i определяет умножение.
3. Для определения деления используются комплексно сопряжённые числа:
.
Поскольку каждое комплексное число определяется парой действительных чисел, существует естественное геометрическое представление комплексных чисел на плоскости с декартовой системой координат. Каждое комплексное число с = a + bi является вектором, начало которого совпадает с началом системы координат. Конец же вектора имеет координаты (a; b), то есть действительная часть комплексного числа соответствует абсциссе, а мнимая – ординате. Ясно, что сложение комплексных чисел соответствует сложению соответствующих векторов.
Геометрическое представление комплексных чисел легко приводит к тригонометрическому представлению (тригонометрической форме) комплексных чисел, которое является чрезвычайно важным для развития теории комплексных чисел.
Пусть комплексное число с = a + bi представлено вектором (a; b). Длина этого вектора называется модулем комплексного числа и обозначается через │с│. Очевидно, что │с│= 
. Пусть угол наклона того же самого вектора равен φ. Число φ называется аргументом комплексного числа, обозначается через arg с и равно arctg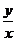 
. Важным обстоятельством является неоднозначность в определении угла. Аргументами комплексного числа можно считать все углы, отличающиеся на 2πk.
Перейдём к непосредственному описанию тригонометрической формы комплексных чисел. Если │с│ = r и arg с = φ, то a = r∙cos φ и b = r∙sin φ. Тогда комплексное число можно представить в виде с = r∙(cos φ + i sin φ). Это и есть тригонометрическая форма комплексного числа.
Эта форма чрезвычайно удобна для умножения и деления комплексных чисел. Пусть с1 = r1∙(cos φ1 + sin φ1 i) и с2 = r2∙(cos φ2 + i sin φ2), тогда произведение вычисляется по формуле с1∙с2 = r1∙r2 (cos (φ1 + φ2) + i sin (φ1 + φ2)), а частное – по формуле 
(cos (φ1 – φ2) + i sin (φ1 – φ2)). Для возведения комплексного числа в степень можно использовать формулу Муавра: сn = (r∙(cos φ + i sin φ))n = r n∙(cos nφ + i sin nφ)). Наконец, тригонометрическая форма комплексного числа позволяет извлекать из комплексных чисел корни. При извлечении корня n-й степени получается n различных значений:
, где k = 0, 1, … n – 1.
Комплексные числа позволяют построить теорию функций комплексного переменного. В частности все элементарные функции могут рассматриваться как функции комплексного переменного. Для перехода от функции действительного переменного к функции комплексного переменного используются ряды Тейлора.
Рассмотрим ряды Тейлора трёх функций
,
,
.
Подставим в первый ряд вместо х мнимое число iφ. В двух остальных рядах заменим х на φ. Второй ряд умножим на i и сложим с третьим. В результате будет получен первый ряд. Таким образом, верна формула Эйлера: 
. Из неё следует, что 
и 
.
Это обстоятельство используется для нахождения действительных решений линейных однородных уравнений.
Пример. Найти действительные решения уравнения у′′ + у = 0.
Характеристический многочлен λ2 + 1 имеет корни i и –i. Следовательно, общее решение имеет вид у = с1еix + c2е–ix. Положив с1 = с2 = ½ получим, что у = cos x. Положив с1 = 
и с2 = – получим, что у = sin x. В итоге действительные решения исходного уравнения имеют вид у = р1∙cos x + р2∙sin x.
