Определение расстояния от точки до прямой.

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую.

 

Для решения задачи необходимо построить проекцию прямой на плоскость ей перпендикулярную (Преобразование 2).

 

 

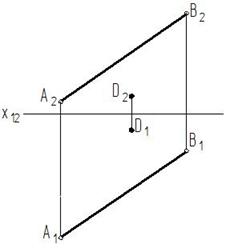
П₄ || l ( AB ): x ₁₄ || (A ₁ B ₁).

Прямая ( AB ) проецируетсявнатуральнуювеличину (A ₄ B ₄ = AB ), точка D в точку D ₄.

D₄E₄ ^ A₄B₄.

П ₅ ^ П ₄; П ₅ ^ AB: x₄₅ ^ A₄B₄.

Прямаяпроецируетсяна П ₅ вточку A ₅ = B ₅ = E _5, а точка D в точку D ₅.

Длинаотрезка D ₅ E ₅ соответствует расстоянию от точки Dдо прямой AB. [ D ₅ E ₅ ]=| DE |

 

 

Проекция плоскости на плоскость ей перпендикулярную (Преобразование№3).

 

Плоскость проецируется в прямую на плоскость ей перпендикулярную

П₄ ^ (DАВС), П₄ ^ П₁ Þ П₄ ^ h Þ х_1,4 ^ h₁

 

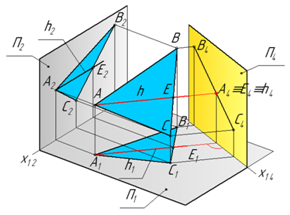
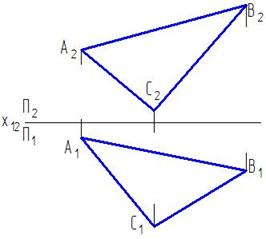
1. Вплоскости ABC проводимгоризонталь h (AE) и задаем плоскость П₄ перпендикулярно ей.

2. Ось x ₁₄ проводим перпендикулярно h ₁ (A ₁ E ₁). Треугольник роецируется на плоскости П₄ в прямую A ₄ B ₄ C ₄.

Определениерасстоянияотточкидоплоскости

 

 

 

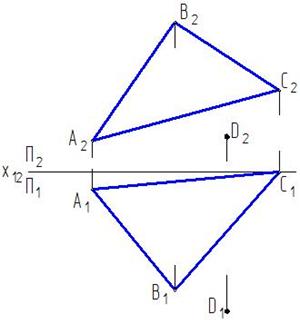
1. Строимпроекциюплоскости (ABC) на плоскость ей перпендикулярную(Преобразование№3)).

2. Проводим в плоскости (ABC) фронталь f

( A ₁) изадаем П₄ перпендикулярно ей: x ₂₄ ^ f ₂

3. Треугольник проецируется на П4 в прямую A ₄ B ₄ C ₄.

4. Строимпроекцию D ₄ точки D на плоскости П₄.

5. Източки D ₄ опускаем перпендикуляр на A ₄ B ₄ C ₄ для определения точки E ₄.

Длинаотрезка D ₄ E ₄ соответствует расстоянию от точки D до плоскости ABC

Проекция плоскости на плоскость ей параллельную(Преобразование№4).

П₄ ^ ( D АВС), П₄ ^ П₁ Þ П₄ ^ h

П₅ II (DАВС), П₅ ^ П₄

Величинатреугольника A ₅ B ₅ C ₅ соответствует натуральной величине треугольника ABC

 

 

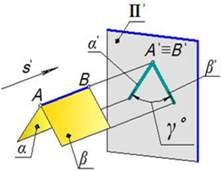
Величина двугранного угла между плоскостями соответствует линейному углу, находящемуся в плоскости перпендикулярной этим плоскостям и их линии пересечения

 

Задача. Определить угол между плоскостями ABC и ABD.

Необходимо построить ортогональную проекцию двугранного угла на плоскость перпендикулярную линии их пересечения

(Преобразование №2 ).

_1. Строим проекцию треугольника на плоскость П₄

П ₄ ^ П _{1 ;} П ₄ || (AB): x₁₄ || (A₁B₁)

2. Задаем новую плоскость проекций П₅

П ₅ ^ П ₄; П ₅ ^ (AB): x₄₅ ^ (A₄B₄)

 

Проекцияугла D ₅ A ₅ C ₅ соответствует величине угла между плоскостями ABC и ABD

 

 

 

 

 

 

ПОВЕРХНОСТИ

Кинематический способ формирования поверхности.

 

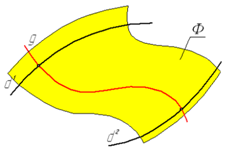Поверхность рассматривается как непрерывное множество последовательных положений линии, перемещающейся в пространстве по определенному закону

 

 

Определитель поверхности - совокупность независимых условий, однозначно задающих поверхность. Состоит из двух частей: Ф{(Г)(А)}

Геометрическая часть (Г) – перечень геометрических фигур, участвующие в образовании поверхности: образующая и другие точки, линии, поверхности.

Алгоритмическая часть (А) – закон перемещения и изменения формы образующей.

Если образующая является прямой линией, которую можно однозначно задать двумя точками или точкой и направлением и графически не изображать, в отличие от кривой линии, то ее обозначение выносят за пределы геометрической части определителя Ф{ g (Г)(А)}

Каркас поверхности - множество точек и линий, определяющих поверхность

 

b j=Ф∩Tj, j =1,2,3,…,n

a i=Ф∩Гi, i =1,2,3,…,m

Ф{ a i, b j }

Очерк поверхности - это линия пересечения плоскости проекций с проецирующей поверхностью, касательной к заданной поверхности и ее обертывающей.

 

 

 

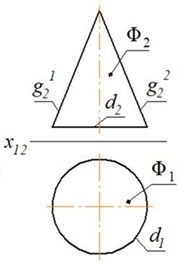
В зависимости от формы образующей, поверхности можно разделить на:

Линейчатые поверхности Þ образующая поверхности – прямая линия

Нелинейчатые поверхности Þ образующая поверхности – кривая линия

Линейчатые поверхности с одной направляющей называются торсовыми (торсами)  – коническая, цилиндрическая, плоскость.

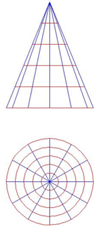
Поверхности вращения

 

Поверхность вращения формируется путем вращения образующей вокруг оси.

При вращении каждая точка образующей формирует окружность, которую называют __________________________.

Параллель с наибольшим радиусом R_max называется ______________________.

Параллель с наименьшим радиусом R_min называется ______________________.

Осевая плоскость параллельная фронтальной плоскости проекций называется ________________________________________________________.

Образующая, принадлежащая главной меридианальной плоскости, называется ________________________________________________________. На фронтальной плоскости проекций эта образующая является очерковой.

Точка на поверхности

 

Точка принадлежит поверхности, если она принадлежит линии, принадлежащей этой поверхности А Î Ф Û________________

Линия l должна на проекциях иметь наиболее простую геометрическую форму: __________________________________ (по возможности)

Пирамида (многогранник). Каждая грань – отсек плоскости. В качестве вспомогательных линий используют прямые. Построение точки на грани сводится к построению точки на плоскости.

Коническая поверхность вращения. Линейчатая поверхность вращения. В качестве вспомогательных линий можно использовать образующую (прямую) или параллель (окружность).

Сферическая поверхность. Нелинейчатая поверхность вращения. В качестве вспомогательных линий используют только параллели (окружности).

 

Линия на поверхности

Линия принадлежит поверхности, если все множество ее точек принадлежит этой поверхности.

Следовательно, чтобы построить линию на поверхности, необходимо представить линию, как множество точек, и построить каждую точку этого множества, используя условие принадлежности точки поверхности.